基于区间数的履带车辆制动方案模糊综合评价

房　远　张豫南　张舒阳　杨怀彬　朱　昊

（装甲兵工程学院，北京 100072）

基于区间数的履带车辆制动方案模糊综合评价

房远张豫南张舒阳杨怀彬朱昊

（装甲兵工程学院，北京 100072）

针对履带车辆制动方案形式和结构多样，难以进行定量分析和有效评价的问题，提出基于区间数的履带车辆制动方案模糊综合评价方法。提出了履带车辆制动方案评价指标层次，根据区间数判断矩阵的概念得出权重向量，应用不同的指数型隶属度函数确定各指标的隶属度矩阵，最后综合得出各方案的最终分数，并据此得出最优方案。实例计算表明该方法具有实用性，为科学研究和实际应用提供了理论依据。

履带车辆制动区间数评价模糊层次分析

引言

随着履带车辆吨位、速度的不断增加，以及对其行驶平稳性与行驶环境适应性要求的日趋严格，履带车辆行走系统与传动系统技术不断改进，其制动系统设计的难度正逐步增大［1-2］。优良的制动能力配合现有的火控系统能够实现有效的短停射击，提高首发命中率；同时急停急起和减速机动可以降低被穿甲弹命中的概率［3］。

制动方案评价是一个多因素评价问题。针对上述现状和特点，建立指标体系，明确各因素的影响程度，进行多因素的综合评价研究，具有重要意义。

结合模糊综合评价理论，本文提出基于区间数的履带车辆制动方案模糊综合评价方法，首先将区间数理论与传统层次分析法结合，并应用区间数权重点值化方法［4］，确定各评价指标的权重；然后利用不同的指数型隶属度函数确定3种履带车辆制动方案中指标值的隶属度矩阵；最后对各制动方案进行模糊综合评价来确定最终得分。该方法应用区间数理论，有效减少了传统层次分析法中主观因素对确定权重的影响，用区间来代替一个数，使得确定的权重更加客观合理。同时，对指标类型进行分类，对不同类型的指标应用有针对性的不同的隶属度函数，得出接近真实情况的隶属度矩阵。

1　基于区间数的层次分析法建模

1.1建立标准层次分析模型

以履带车辆制动相关的文献资料为基础，根据标准层次分析法的建模步骤，建立履带车辆制动方案评价的层次结构模型如图1所示。

图 1履带车辆制动方案评价层次结构模型

1.2确定单项指标的权重

（1）构造判断矩阵。设指标个数为，指标体系某层指标集为C=｛C1，C2…Cn｝，专家的判断矩阵为A=（aij）n× n，aij表示指标Ci和Cj的重要性比值，其中为区间数，和分别为下限值和上限值。则基于区间数的判断矩阵A可以描述为

采用基于区间数的9标度的方法，见表1，测量结果表现为正互反矩阵。

表1　基于区间数的判断矩阵1～9标度法的含义

（2）计算指标的区间数权重。令 wl和wu分别代表［alij］和［auij］的最大特征根的具有正分量的归一化特征向量，则单个区间数判断矩阵A的区间权向量可表示为

式中，wn为区间数权重

（3）区间数权重点值化。设专家人数为m，则针对某一指标的归一化权重矩阵W可表示为：

则n个指标的相对权重集为：

（4）一致性检验分析

设区间数判断矩阵A=（aij）n× n的模糊度为

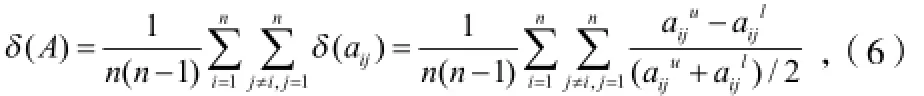
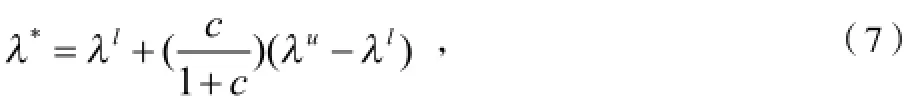
则基于区间数的判断矩阵的一致性判断标准为［5］：

式中的R.I.取值如表2所示。

表2　判断矩阵的值

1.3计算整体权重

将分层后各指标的权重进行自下而上的线性加权运算，求得最底层要素相对于最高层总目标的整体性相对权重。

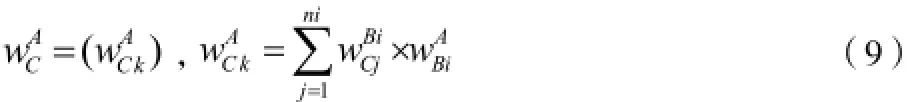
其中k=1，2，…，p，k值随i值变化而变化。

2　模糊综合评价

2.1评价指标集U

设U=｛u1，u2，…，un｝为刻画被评价对象的n种因素。其中ui为评价指标，i=1，2，…，n，n为应用模糊原理进行综合评价的单个指标的个数，集合U是模糊评价的基础。

2.2评语集V和分数集S

设评语集为V=｛v1，v2，…，vm｝为刻画每一因素所处状态的m种决断，相应的评价分数集为S=｛s1，s2，…，sm｝，m为评价等级或评价档次数。

2.3模糊评价矩阵

以评语集V为标准，对U中的每一单因素指标进行模糊评价，所得矩阵即为模糊评价矩阵（隶属度矩阵）R，R中元素即为相对应指标的隶属度。对单因素 u（ii=2，3，…，n）进行评价，根据评价等级vj（j=1，2，…，n）确定隶属度rij，如此可得到第i个因素ui的单因素评价集ri=｛ri1，ri2，…，rim｝，即有R=（rij）m× n。

2.4改进的指数型隶属度函数

设x为经评价后得到的指标值，u（x）为x的隶属度函数，H（ii=2，3，…，n）是评价指标区间内确定的n个递增非负特征值。下降型指数型隶属度函数和上升型指数型隶属度函数分别如式10和式11所示。

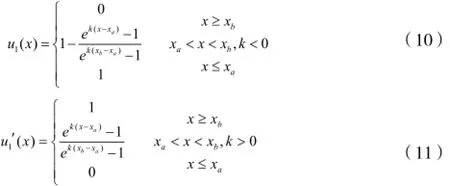
以下降型指数型隶属度函数为例，则评价指标对评语集V的隶属度函数u1（x），u2（x），…，un（x）为：

2.5综合评价结果

履带车辆制动方案评价的最终结果为

式中，W为权重向量，R为模糊评价矩阵，Z为综合属性值，P为制动方案的最终综合属性值。

3　算例分析

以履带车辆制动系统发展现状和发展趋势为参考，选出3种典型的制动方案，应用模糊层次分析法进行综合评价。3种制动方案为，方案一：机电联合制动；方案二：机械制动提供较小制动力，液力制动提供较大制动力；方案三：机械制动提供较大制动力，液力制动提供较小制动力。

3.1建立履带车辆制动方案评价指标体系

以国家相关试验规定为参考［6］，将制动初速度设为65 km/h，据此得出的制动指标称其为“基础制动能力指标”。其中A4项“制动系统反应时间”，为了体现不同制动方案的制动特点，将时间仅计算为电制动或液力制动的反应时间，而忽略3种方案共有的机械制动的反应时间（若采用液压辅助制动装置，反应时间仅为0.03s～0.05s，可以忽略不计［7］）。

经初步筛选，选取意义重大且容易定量化的指标，建立履带车辆制动方案综合评价指标体系见表3。

表3　履带车辆制动方案综合评价指标体系

3.2确定C层评价指标的权重

（1）选择5位专家，对指标体系进行基于权重数的求解。针对表3的一级指标B1项，以专家1给出的互反判断矩阵A1为例，

（2）根据式（6）（7）（8）对A1进行一致性检验，计算得C. R.=0.0688≤0.1（1+δ（A））=0.1406成立，可知满足一致性检验条件。根据式（2）（3）（4）并进行归一化，可得根据A1计算得出的 C1～C5点值化相对权重向量为 wl*= （0.3431，0.1643，0.0663，0.3072，0.1191）。同理，计算其余4位专家给出的 A2～A5，并根据式（5），得出B1项指标的综合相对权重为

同理，建立B2-C，B3-C，A-B的判断矩阵并求得对应各指标的权重w，其结果见表4。

（3）应用公式（7）计算出C层各指标对于A的权重，见表4。

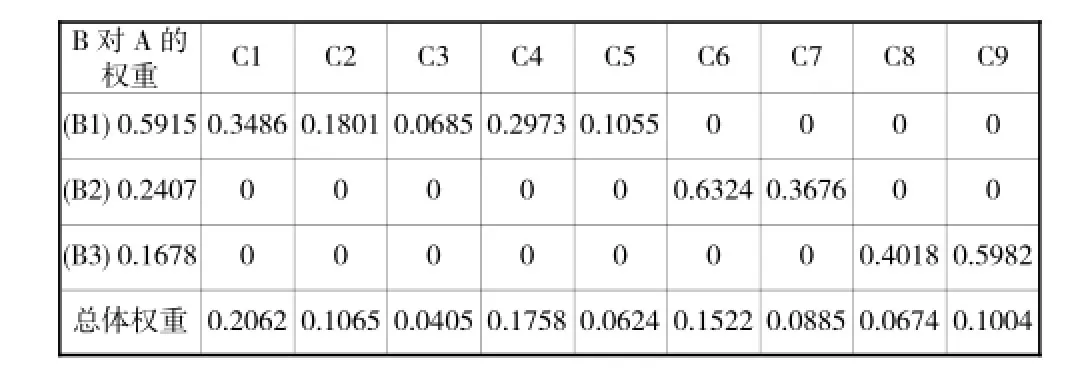
表4　各层指标的单项和综合权重

3.3单因素隶属度的确定

（1）3种制动方案针对C1～C9指标的具体数值如表5所示。需要进行说明的是，方案一（机电联合制动）还没有实际的成熟车型，因此表5中方案一的部分数据来源于仿真研究，采用电机和机械制动的联合制动；方案二、方案三的数据和方案一的部分数据来源于公开的书籍、文献和互联网资料，并依据专业领域的基础知识对其进行了修正。

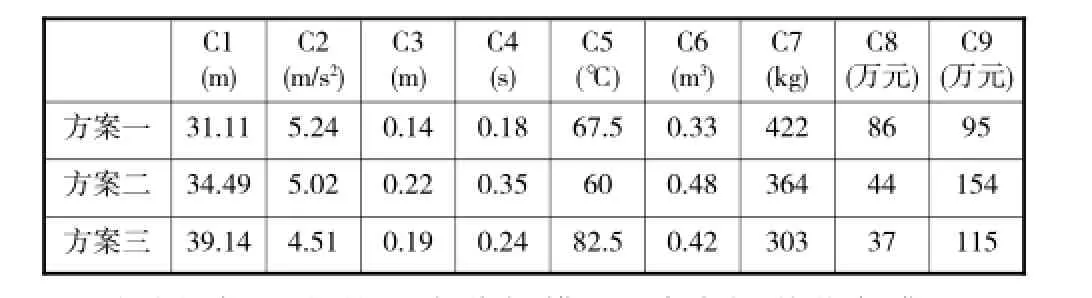
表5　三种方案的具体数值

（2）根据上文的层次分析模型，确定评价指标集。U= ｛C1，C2，C3，C4，C5，C6，C7，C8，C9｝，按照评价由高到低的顺序确定评语集为V=｛优秀，良好，一般，较差，差｝，对应的分数集确定为S=｛95，85，75，65，50｝。

（3）C1～C9指标分为2类，第一类是成本型指标（越少越好），包括 C1和 C3～C9，适用式（10）所示的隶属度函数；一类是效益型指标（越多越好），包括C2，适用式（11）所示的隶属度函数。下面以C1为例，计算隶属度。

为使计算得出的不同指标的隶属度更加客观可信和有针对性，不同指标需要设置不同的特征值H和系数k。根据C1划分等级，确定5个特征值，有H=｛H1，H2，H3，H4，H5｝=｛30，32，35，39，43｝，确定k=-0.8。根据式（12）～（14），对3种方案，计算出C1项对应的单因素评价集r1见表6。同理可得三种方案的整体隶属度矩阵，如方案一的隶属度矩阵为

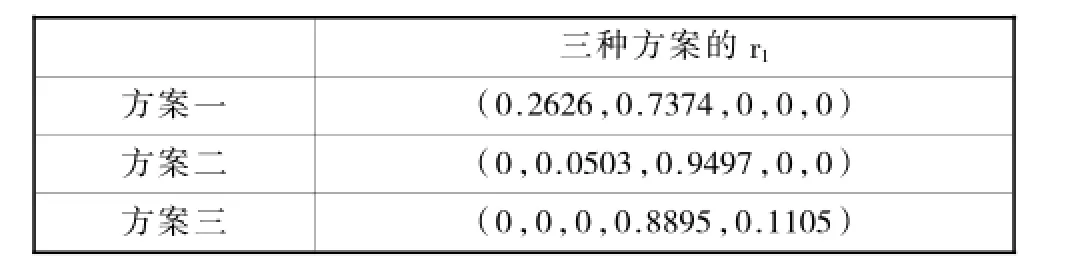
表6　三种方案的单因素评价集

3.4总体综合评价

根据所得的各项指标的权重和隶属度，又由式（15）、（16）可得方案一的综合属性值和最终综合评分为

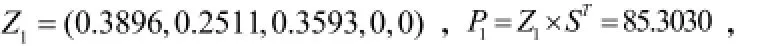
同理，计算得出方案二和方案三的最终综合评分为：P2=82.2497，P3=82.5586。评价结果显示，在本次履带车辆制动方案的评价与选择中，方案一的分数最高，为最佳方案。

4　结论

本文应用基于区间数判断矩阵的模糊AHP法，来解决履带车辆制动方案的综合评价工作，在确定指标权重和评价方案的过程中更加科学合理，减少了主观因素和定性评价的误差和不确定性。实例的计算和分析，取得了较好的评价结果，说明了该方法在履带车辆制动方案评价中的合理性和可靠性，给出了评价履带车辆制动方案的一种新方法。

［1］闫清东，张连第，赵毓芹.坦克构造与设计（上册）［M］.北京：北京理工大学出版社.2006：143-147.坦克装甲车辆 ［M］.

［2］郑慕侨，冯崇植，蓝祖佑.坦克装甲车辆 ［M］.北京：北京理工大学出版社.2006：170-180.

［3］张宇，魏超，霍键鹏，宋卫群.目标减速机动对穿甲弹命中概率的影响分析 ［J］.北京：北京理工大学学报.2011，31（7）：2-8.

［4］庞宾宾.装甲车辆电传动系统评价研究［D］.北京：装甲兵工程学院.2014，12：75-76.

［5］叶跃祥.区间数多属性决策的一些问题研究［D］.合肥：中国科学技术大学.2007，4：33-40.

［6］GJB 59.12-87，装甲车辆试验规程——制动性能试验 ［S］.国防科学技术工业委员会.1987车辆动力学［M］.

［7］宋彬，吕建刚，张培林，王怀光.履带车辆静动液辅助制动系统仿真与实验［M］.北京：国防工业出版社.2015：2-6.

A Fuzzy Comprehensive Evaluation Method for Braking Schemes of Tracked Vehicles Based on Interval Number

FANG Yuan，ZHANG Yunan，ZHANG Shuyang，YANG Huaibin ZHU Hao
（Academy of Armored Forces Engineering，Beijing，China）

In view of the various structures and forms in the evaluation of braking schemes of tracked vehicles and the difficulty in quantitative analysis，a fuzzy comprehensive evaluation method based on interval number is proposed.The evaluation index hierarchy for braking schemes of tracked vehicles evaluation was presented.The weight-vector of interval judgment matrix were calculated.The different exponential type membership functions was used to calculate single factors’membership matrixes.Then these methods are combined to establish integrated indices for all braking schemes of tracked vehicles and make selection of the optimum scheme by comparison of these indices.Application indicates that this is an effective method in solving the evaluation problem involved with many factors and that the proposed method is reliable and practical.

tracked vehicle，brake，interval number，evaluation，fuzzy-AHP

基础产品创新科研项目VTDP-3601。