“平行四边形的面积”教学设计

叶采华

一、教学内容

人教版义务教育教科书《数学》五年级上册第六单元第86—88页。

二、教学目标

1.利用数方格和剪拼等方法，探索并掌握平行四边形的面积计算公式，会用这个公式计算图形面积。

2.通过学生操作、观察、比较，发展学生的空间观念，渗透转化的思想方法。

3.在探索知识的过程中培养学生的合作意识和多向思维的能力。

三、教学重难点

重点：理解平行四边形面积计算公式的推导过程，掌握平行四边形面积的计算方法。

难点：掌握平行四边形与长方形之间的内在联系。

四、教学准备

教师准备多媒体课件、平面图形、剪刀、尺子等教具；每桌两个学生准备一个平行四边形、（每桌的平行四边形不同）方格纸、剪刀、尺子等学具。

五、教学过程

（一）情境导入

出示第86页主题图，从图中找出认识的平面图形。（长方形、正方形、三角形、平行四边形、梯形等）说说哪些图形的面积已经会算了。（长方形、正方形）回顾长方形和正方形的面积计算公式。

（二） 猜测验证

1.出示课件，将长方形和平行四边形的花坛按比例缩小成平面图形，学生目测，比较两个图形的面积哪一个更大？

2.计算长方形的面积。出示课件，测量长方形的长和宽，学生口述出长方形的面积计算方法。（5×3=15平方厘米）板书：长方形的面积=长×宽

3.猜测平行四边形的面积计算方法。这个平行四边形的面积应该怎么求？需要量出哪些数据？学生先想一想，然后拿出尺子量出有关数据，自己计算出它的面积。（学生可能会列式：5×4=20平方厘米）

板书：平行四边形的面积=底×邻边

（三）公式推导

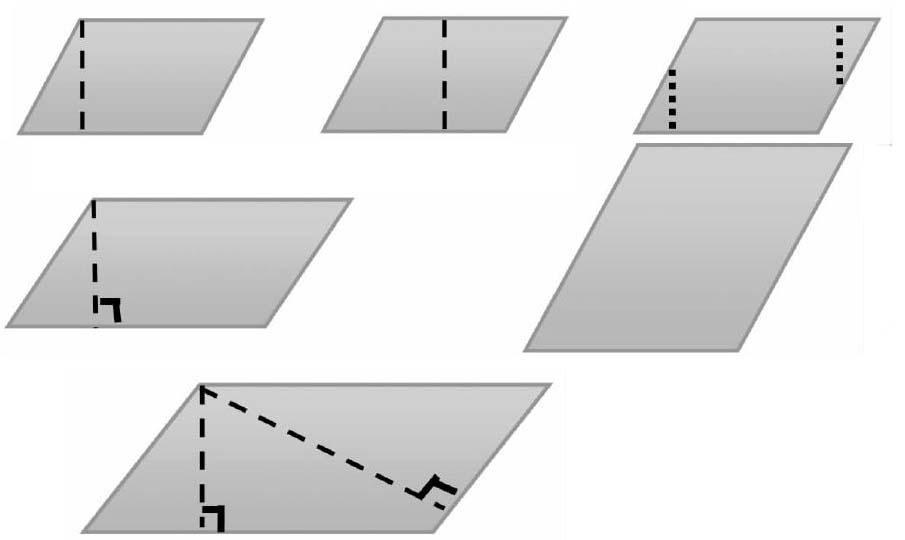
1.动手实践，将平行四边形转化成面积相等的长方形。同桌合作，一边操作一边思考并填空：（1）平行四边形转化成长方形，（ ）不变，（ ）变了。（2）转化后的长方形的长相当于平行四边形的（ ），长方形的宽相当于平等四边形的（ ），因为长方形的面积=（ ），所以平行四边形的面积=（ ）。

2.汇报交流，展示不同的剪拼方法。

3.完成填空题，总结公式。板书：平行四边形的面积=底×高 S = a h

（四）课堂练习

1.计算下面平行四边形的面积。

第二幅图先出现一个平行四边形，没有条件，接下来给出一组不对应的底和高，学生试算，发现不对，明确求平行四边形的面积一定要相对应的底和高相乘。

2.四个数据分别为5、10、6、12，平行四边形的面积是（ ）。

3.求图形的面积。

课件演示：两条平行线，以平行线为底，画一个平行四边形，面积是20平方厘米。再由底边的两个端点出发，画一个形状不同的平行四边形，求它的面积；（20平方厘米，等底等高）再由这两个端点出发，画一个楼梯状的图形，求它的面积；（20平方厘米，渗透转化思想）再由这两个端点出发，画一个三角形。（10平方厘米，感知三角形和平行四边形的联系，猜想以后学习三角形和梯形的面积也可以用转化的方法。）

（五）课堂总结，谈收获。

（六）思维拓展

刚才否定了平行四边形的面积=底×邻边，想一想：底×邻边可以求出什么？

又一次转化，将平行四边形的活动木框拉成一个长方形，发现长方形的面积就是平行四边形的底×邻边，什么变了，什么没变？（这一次的转化面积变大了，周长不变。）（作者单位：江西省萍乡市登岸小学）