刍议初中数学总复习的分层教学

邱称秀

新课程标准指出“数学要面向全体学生，实现人人学有价值的数学，人人都能获得必要的数学，不同的人在数学上得到不同的发展”。由于学生存在基础知识和接受能力的差异，在教学上如果用“一刀切”的办法，会造成一部分学生“吃不饱”而另一部分学生又“吃不了”。所以在教学中要“因材施教”，针对不同层次的学生提出不同的要求，让每个学生都有收获。

一、教学过程分层

要保证所有学生都参与复习课，让各种层次的学生都有所收获。首先，要求学生重温书上的知识，让大家有所准备，在课堂上尽量调动他们的积极性，设计不同难度的问题，用一些比较简单的问题去激发学困生的兴趣。同时，设计一些比较基础、略有难度的问题激发优生的学习动力。最简单的问题首先给学困生表现的机会，鼓励他们来完成，遇到难度较大的问题就鼓励优等生来完成。课堂上还要多用表扬、鼓励的语言去评价学生。

在复习“全等三角形的判定”这一节内容时，为了归纳全等三角形的判定方法。首先，设计了一个情境“比一比谁的记性最好，全等有哪些判定方法？”然后让大家都说一说，说对一条或者两条都给予适当表扬，使学生一进入课堂就有成就感。

在运用这些判定方法时，设计由简单到复杂的题目。

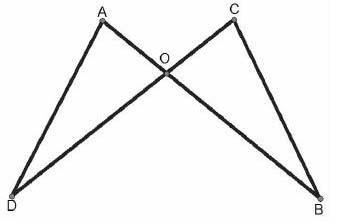
题（1）“已知AB和CD相交于点O，∠A=∠C，AO=CO，求证△AOD≌△COB”这道题图形比较简单，条件问题都很直接。大部分学生一看就知道用“ASA”方法来证。让大家都能拿起笔来做一做。

题（2）针对这个题目引申、拓展，求证：①AD=CB；②∠ADC=∠CBO。（目的是让学生明白要证明边角相等，一般先证三角形全等，再找对应边和对应角相符）

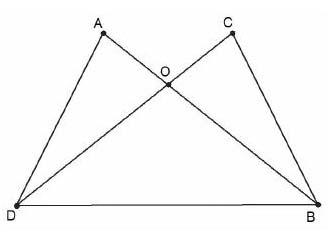
为了让学生能灵活地运用这几种方法，设计题（3）：据题中已知条件要自己再补充一个条件使得两个三角形全等。“如图，AB和CD相交于O，AD=CB，请你补充一个条件使得△AOD≌△COB。”

同时设计题（4）：“如图，线段AB和CD相交于O，AD=CB，AO=CO，DO=BO，△ABD和△CDB全等吗？证明你的理由。”（这个题目条件比较多，图形较复杂，要得到结论比较间接，这道题对中等生较有挑战性。）

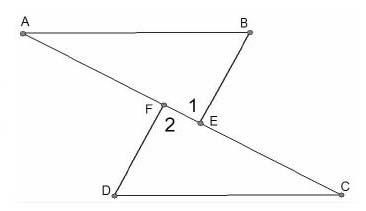
最后设计难度较大的题目，挑战中等生。“如图，点A、F、E、C在同一条直线上，AF=CE，BE=DF，BE∥DF，求证：（1）△ABE≌△CDF；（2）∠A=∠C；（3）AB∥CD。”

尽量让每个学生都参与进去，让大家都有所收获，都去体会上数学课的乐趣。

二、作业分层

为了检验学生对课堂知识的掌握情况，检验复习效果，我们会设计一些相应的作业。题目难度大一些，基础差的学生不会做，或失去信心，或应付完成，或抄袭他人。难度太小，优生认为太简单，能力得不到提升。为了使复习课更有效，必须要关注“两头”学生，尤其要关心学困生，降低对他们的要求，尽量设计简单的题目，同时题量也不能过多。课任教师要准备好一本作业设计本，里面造好两头学生的名单，作业要分层设计。（例如：在复习“因式分解”这一节时，笔者设计的作业如下：

（1） 填空题：1.因式分解就是把一个 化成几个整式 的形式的过程，因式分解的方法有 ， 和十字相乘法。

三、辅导分层

分层辅导学生可以加深学生对知识的理解，各层次学生可以利用教师辅导的机会及时解决自己头脑中的问题。

数学知识具有很强的连贯性，如果前面的知识没有理解，在学习新知识时就不会完全掌握。对于学困生的辅导，要强调新旧知识的连贯，帮助学困生巩固以前的知识，理解并简单运用新知识。对于中等生，要强调对本节知识的巩固掌握，采取练习的形式来加深他们对新知识的理解。对于优生，除了帮助他们进一步巩固新知识以外，主要强化他们对本节知识和其他已有知识的综合应用，以及与后续知识的联系。简而言之，“扎实旧知识”—“巩固新知识”—“新旧知识的综合应用与后续知识的联系”。分层辅导如果做得好，可以起到事半功倍的教学效果。（作者单位：江西省于都县高龙中小学）