三角函数图象与性质应用常考题型及规律破解
◇ 山东 王桂翠
三角函数图象与性质应用常考题型及规律破解
◇山东王桂翠
三角函数图象及性质应用是高考重点题型,其中既有选择题也有解答题.现将三角函数图象及性质应用的常考题型及规律破解总结如下,供同学们学习时参考使用.
1 结合图象变换解决给值求角问题


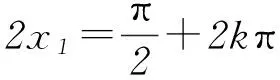
规律破解三角函数求值有以下3类:
1)“给角求值”,一般所给的角都是非特殊角,解题时要利用所给关系,结合公式将一般角转化为特殊角求解.
2)“给值求值”,给出某些角的三角函数式的值,求另外一些角的三角函数值,解题规律在于“变角”,将题目中涉及的角化为同角或具有某种关系.
3)“给值求角”,实质是转化为“给值求值”,先求角的某一函数值,再利用角的范围来确定角.
2 结合三角函数图象解决函数值大小问题

Af(2) Bf(0) Cf(-2) Df(2) ω=2,f(x)=Asin(2x+φ). 规律破解对于三角函数中比较大小的问题,一般步骤是: 1) 根据题中所给的条件写出三角函数解析式,如本题通过周期判断出ω,通过最值判断出φ; 2) 需要比较大小的函数值代入解析式或者通过函数图象进行判断,本题代入计算易求解,故可以根据函数图象特征进行大小判断. (1) 求函数f(x)的解析式,并求其图象的对称轴方程; (2) 已知关于x的方程f(x)+g(x)=m在[0,2π)内有2个不同的解α、β. (ⅰ) 求实数m的取值范围; (2) (ⅰ) 由(1)可知 f(x)+g(x)=2sinx+cosx= 其中 总之,高考对三角函数图象与性质的考查主要体现在以上3种题型,有时还会在知识的交会点命题,但只要抓住问题考查的本质,弄清楚解题规律,即可迎刃而解.在平时学习中要加强这方面训练. 山东省青岛经济技术开发区第一中学)

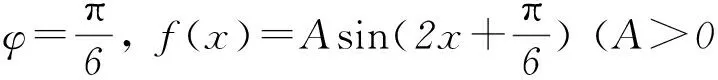

3 结合三角函数图象解决求值及证明问题