数学思想方法在解题中的应用
2016-09-28 06:53:16江苏侍昌亚
高中数理化 2016年17期
◇ 江苏 侍昌亚
数学思想方法在解题中的应用
◇江苏侍昌亚
数学思想方法是数学知识、数学思维、数学能力的本质体现.在数学解题中,缺乏数学思想方法的有效引导,解题易陷入束手无策、无从下手的局面.对此,笔者从平面向量知识点出发,略谈数学思想方法在解题中的应用,以供参考.
1 巧用转化思想,优化解题
转化思想,即把问题从一种形式转化为另一种形式,从而找出问题突破口的一种数学思想方法.转化思想是数学研究中克服难关的有效手段,具有一定的灵活性和多样性,有助于发散思维,培养解题能力.

(1) 当a∥b时,求cos2x-3sin 2x的值.
(2) 求f(x)=(a+b)·b的最小正周期和单调递增区间.



2 把握特殊化思想,巧妙解题
特殊化思想是解数学选择、填空题中常用的一种思想方法,在解题过程中通过选取符合题意的特殊值、特殊位置、特殊方程、特殊图形以及特殊向量等方式,使问题化难为易、化繁为简.

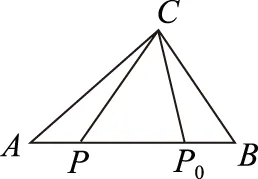
图1
AAC=BC;
B∠ABC=90°;
C∠BAC=90°;
DAB=AC

图2

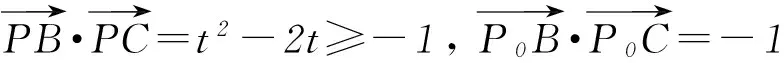
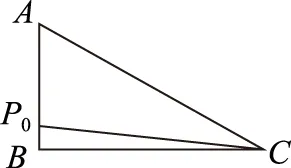
图3

同理可判断选项C、D错误.

3 注重数形结合,直观解题
数形结合思想是数学解题中常用的数学思想方法之一,融合了形象思维和抽象思维,其实质是将抽象乏味的数学语言与直观形象有机地结合起来.

|2a-b|的最大值、最小值分别是________.
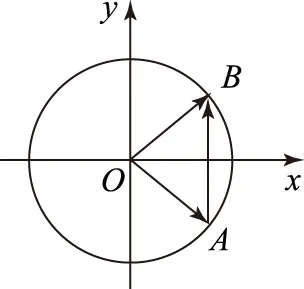
图4


盐城市亭湖高级中学)
猜你喜欢
中学数学研究(广东)(2022年9期)2022-06-16 06:30:22
中学生数理化·七年级数学人教版(2022年4期)2022-04-26 14:31:08
理科爱好者(教育教学版)(2022年1期)2022-04-14 22:07:50
中等数学(2021年5期)2021-08-14 02:31:06
中学生数理化·七年级数学人教版(2021年4期)2021-07-22 03:16:04
中学生数理化·中考版(2020年12期)2021-01-18 06:59:40
新高考·高二数学(2019年2期)2019-09-05 11:15:09
小学生学习指导(低年级)(2018年6期)2018-05-25 01:42:26
数学学习与研究(2016年19期)2016-11-22 11:06:48
中学生数理化·高一版(2016年5期)2016-05-14 09:03:47

