电除尘器电流体动力学流动与极间干扰的数值模拟研究

周小颖，窦华书，陈小平

(浙江理工大学机械与自动控制学院，杭州 310018)



电除尘器电流体动力学流动与极间干扰的数值模拟研究

周小颖，窦华书，陈小平

(浙江理工大学机械与自动控制学院，杭州 310018)

对单电极和多电极电除尘器内部流动建立了三维数值模型，研究了电流体动力学(EHD)流和极间干扰对电除尘器内部流动特性的影响。电场分布由泊松方程和电流连续性方程控制，气体流动由三维不可压缩的Navier-Stokes方程结合标准k-ε湍流模型来描述，气体流动和电场通过库仑力耦合计算。模拟结果显示：EHD流使得电极前后分别形成两个对称的涡，随着气流进口速度的提高，上下涡核朝相反的方向移动；EHD流通过同时提高湍流耗散率和湍动能的生成来影响湍流强度，其结果取决于哪个作用占优势。结果发现：电极之间会产生极间干扰，中间电极前后由于电势和空间电荷密度分布的挤压作用使得涡强度明显减小，并且结构更规则。

电除尘器；收集效率；电流体力学；电场力

0　引　言

电除尘器(electric precipitator, ESP)是一种使用广泛的高效除尘设备，通过对颗粒充电并使颗粒在电场力驱动下向收集板移动，以达到除尘的目的，其除尘效率可达99.9%以上[1]。在电除尘器工作过程中，中性的气流也会与通道中的带电离子发生动量交换，产生电流体动力学(electro-hydrodynamics, EHD)流，影响流体的气流形态和运动特性[2]。

研究人员对EHD流进行了大量实验和数值方面的研究[3]。Farnoosh等[4]利用混合有限元-通量修正输运法(FEM-FCT)模拟电场分布，采用有限体积法模拟气场分布，以此来建立EHD流的三维数值模型。Zhao等[5]通过采用混合有限元-特征法(FEM-MOC)数值方法来分析EHD流动。Podlinski等[6]和Chang等[7]先后采用PIV(particle image velocimetry)技术测量了不同EHD数和雷诺数下的流场速度。Leonard等[8]通过实验研究线-板型电除尘器内部的EHD二次流和湍流场，采用纹影显示法(schlieren visualization)和激光测速法(laser anemometry)来显示一个垂直于放电极的平面上非湍流的二次流。然而，由于EHD流具有复杂的随机性，关于其对电除尘器内部特性的影响作用，研究人员尚未达成一致的意见，一些研究人员甚至给出了相反的结论[9-10]。同时，大部分的研究集中在EHD流对气流形态和颗粒收集效率的直接关系上[11-13]，对内部气动参数的定量分析较少，对于极间干扰现象也没有系统的研究，而这些研究对于深入了解EHD流的规律十分重要。

本文在已有研究基础上对EHD流进行数值研究，定量分析了EHD流对电除尘器内部速度分布、湍流强度、气流流线以及涡流特性的影响，并研究了多电极情况下，极间干扰下对电极附近气动特性的影响。

1　数值计算方法

为了对电流体动力学流和极间干扰进行数值研究，需要对电场分布和气流场分布进行耦合计算。其中，电场控制方程为泊松方程和电流连续性方程，分别模拟电势分布和空间电荷密度分布；气场控制方程为不可压缩的Navier-Stokes方程，采用标准k-ε湍流模型来封闭方程组。通过对气流动量方程添加与电场库仑力有关的源项来表现EHD流。

1.1电场模型

电场数值模型的建立基于以下假设：放电稳定，电场分布和空间电荷密度分布不随时间变化；带电离子电极单一，离子迁移率为常数。电场分布计算采用软件FLUENT 14.5，通过编写用户自定义程序(user-defined function, UDF)嵌入软件的方式进行计算。电场分布的控制方程为电势泊松方程和电流连续性方程[14]：

泊松方程：

(1)

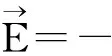
(2)

电流连续性方程：

J=0

(3)

(4)

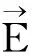
1.2气流模型

EHD流由荷电离子与气流的动量传递引起，本文通过对气流运动的动量方程添加源项来描述EHD流。气场分布由FLUENT14.5计算，源项添加的方式为自主编程。气流运动的控制方程为雷诺平均的Navier-Stokes方程[15]：

(5)

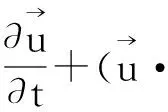
(6)

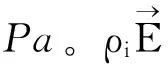
采用基于Boussinesq假设的标准k-ε湍流模型来封闭Navier-Stokes方程组，控制方程如下[15]：

Gk+Gb-ρ ε

(7)

(8)

其中：k和ε分别为湍动能及其耗散率；Gk和Gb为基于平均速度梯度、浮力产生的湍流动能；σk和σε分别是k和ε的湍流普朗特数；C1ε、C2ε、C3ε、σk、σε及Gμ均为常数。湍流粘性系数由下式计算：

(9)

2　结果与讨论

2.1单电极电除尘器内EHD流的影响分析

2.1.1几何模型与边界条件

为了研究单电极电除尘器内部EHD流对气动特性的影响，建立图1所示的几何模型。X、Y、Z分别表示流向、收集壁面法向和沿放电极方向；原点坐标如图1所示；除尘器通道长度L为0.5m，入口宽和高(W×H)为0.1m×0.1m。放电极设置在通道中央，直径为2mm。网格划分采用O型网格，总网格数为817600。

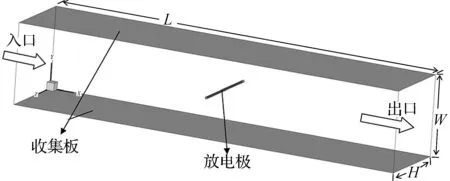
图1　单电极电除尘器几何模型

表1列出了完整的边界条件，设置数值与文献[10]一致。入口进气速度分别为0、0.2、0.5、1.0m/s，入口湍流强度设为5%。

表1　边界条件

2.1.2计算结果分析

图2给出了Z=0 m截面上的电势分布和空间电荷密度分布。可以看到，电势呈横向椭圆形分布，纵向梯度值大于横向梯度值，而空间电荷密度呈椭圆形分布，横向梯度值高于纵向梯度值。

图2　单电极除尘器中心截面电势云图与空间电荷密度云图

图3　不同入口速度下中心横截面上的气流流线

图3给出了入口气流速度为0、0.2、0.4、0.5、1.0 m/s条件下，中心横截面上的流线图，流线形状与文献[10]计算一致。从图3(a)观察到，没有气流进入除尘器时，即u=0 m/s时，整个通道区域形成4个大涡，4个大涡成中心对称分布，几乎占据整个通道区域，进出口处有回流产生。当入口气流速度增大到0.2 m/s，涡的尺寸变小，上游涡向两边分散，下游涡向中心集中。当速度到达0.5 m/s时，下游的涡先消失，上游的涡粘附在收集壁面上。速度继续增大，涡完全消失。可以发现，随着速度的增加，上游涡的涡核向靠近收集板的方向移动，而下游涡的涡核朝靠近放电极的方向移动。

为定量观察内部流场特性，对放电极截面的中心线(Z=0，X=0.25 m)上的数据进行分析。图4给出了u=0.5 m/s时，有无EHD流情况下，气流场内各向速度、湍流强度、静压、湍流耗散率和k值增量的分布。由图4(a)可以发现，有EHD流时，放电极与收集板之间的速度梯度明显增大，放电极处的速度提高50%左右，近收集板处的速度降低，有速度波动。由图4(c)和(d)看到，EHD流使得Y方向和Z方向的速度提高，其中Y方向的速度有利于气流向收集壁面流动，Z方向的速度决定涡的纵向方向。由图4(e)-(g)可以发现，EHD能同时提高湍流耗散率和湍动能的生成，两者综合决定了EHD流对湍流强度的影响是增强还是减弱。此工况下EHD流对湍流强度有增强作用，特别是在收集板附近，湍流强度提高了2～3倍。此外，由图4(h)可以发现，近收集壁面处静压值几乎无变化，但放电极处静压降低，分布呈V型。

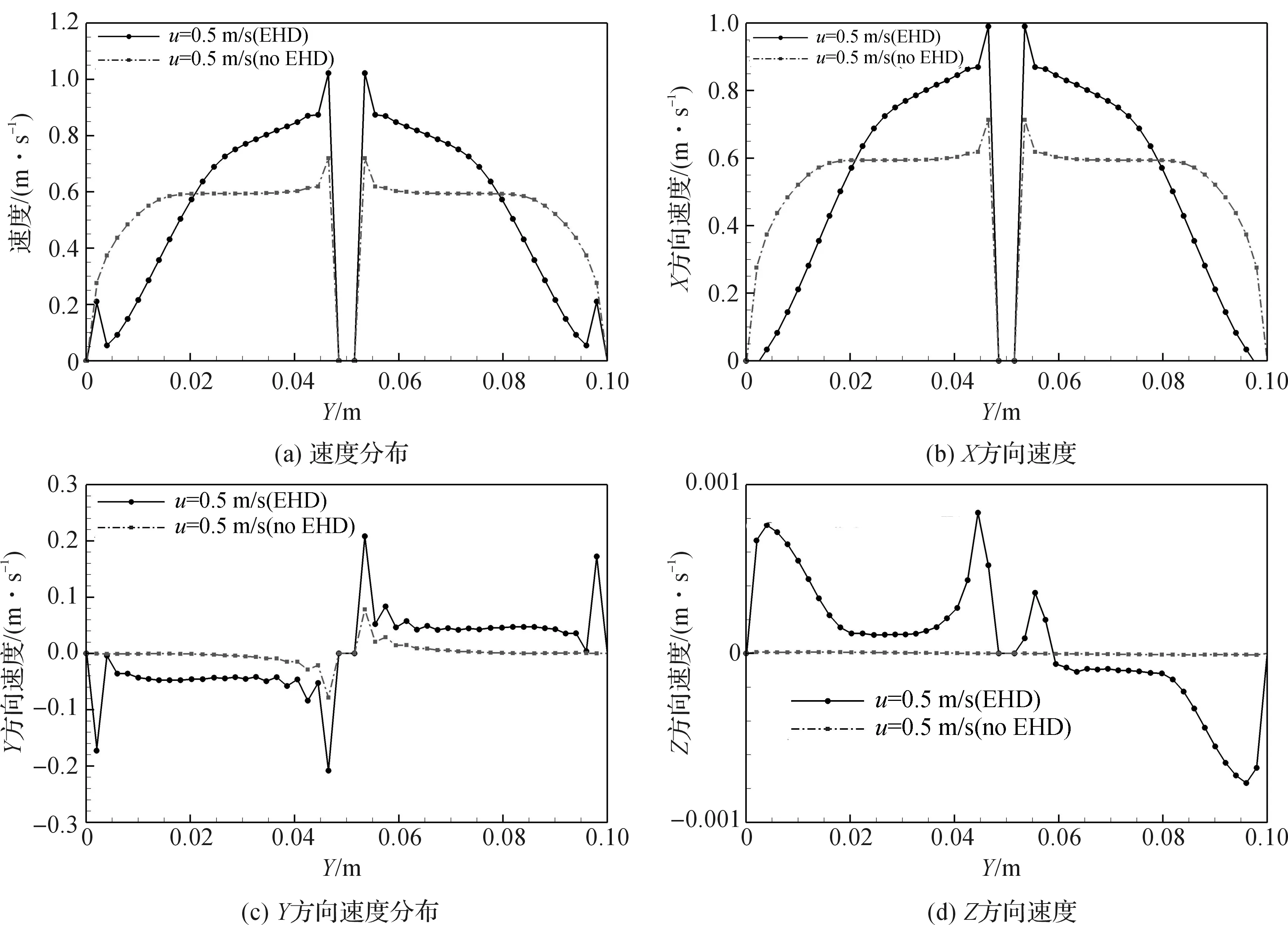
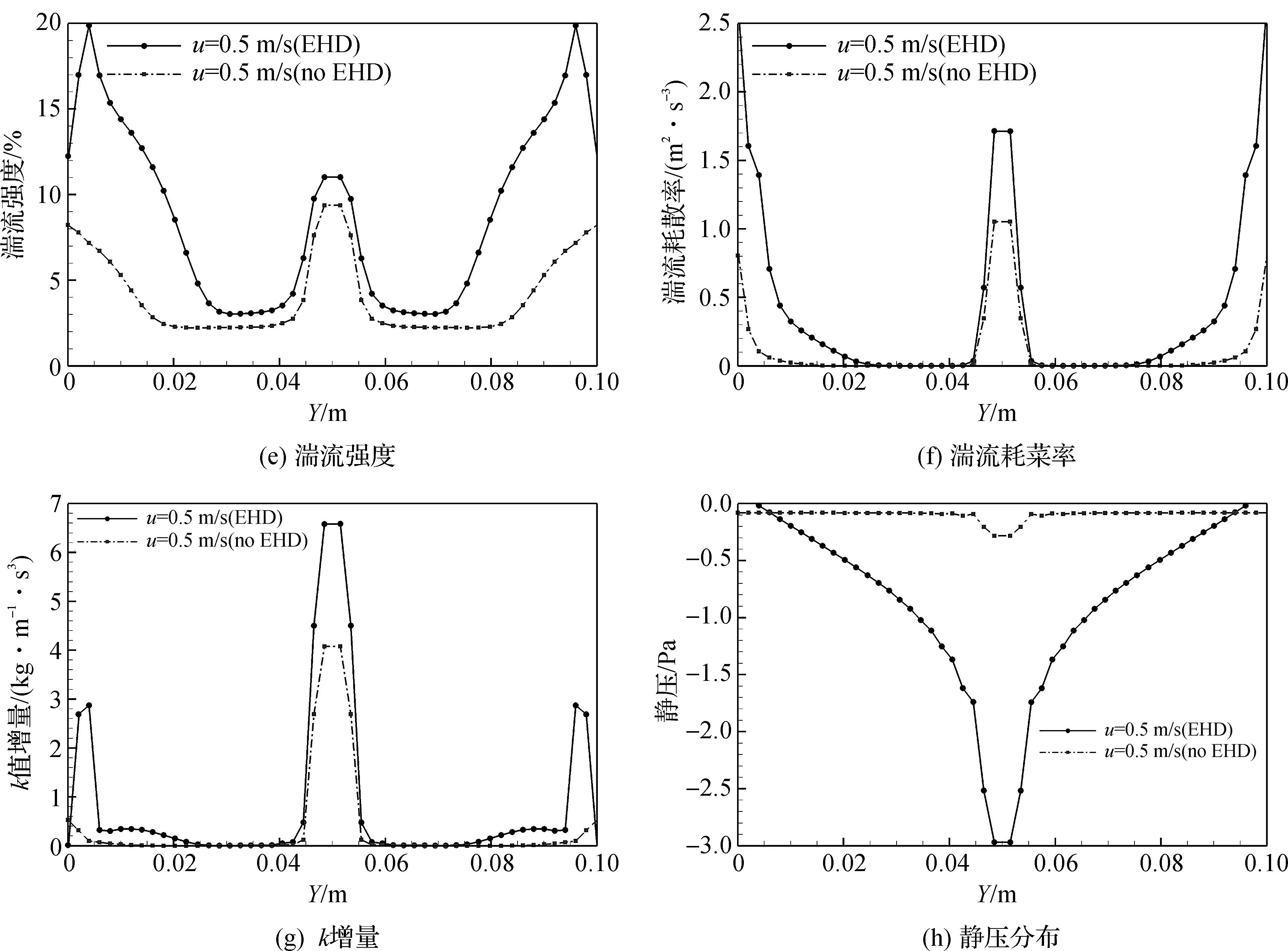
图4　u=0.5 m/s，放电极处截面的中心线(Z=0 m，X=0.25 m)上的速度分布、X方向速度、Y方向速度、Z方向速度、湍流强度分布、湍流耗散率、k增量分布、静压分布

2.2多电极除尘器极间干扰研究

在图1所示的单电极干式电除尘器的几何模型基础上，建立相同入口面积、放电极直径、极间距、极-板间距的多电极干式电除尘器几何模型。出口与入口部分长度不变，保持0.25 m，放电极数量增加到3个，通道总长度L为0.7 m。

图5给出了三电极电除尘器Z=0横截面上电势与空间电荷密度分布云图(X=-0.23～0.23 m)。由图5(a)发现放电极周围椭圆形电势分布连成一片，两电极中点处电势最低。从放电极到收集板，电势在Y方向呈层状递减分布，靠近收集板处分层明显。由图5(b)发现放电极之间空间电荷密度分布呈相抵的状态，电极周围空间电荷密度的环状分布被压缩，椭圆分布横向直径减小，特别是第二个放电极，分布云图压缩明显。放电极连线的中点位置，空间电荷密度几乎为零。

图5　三电极电除尘器内部电势与空间电荷密度分布云图

图6给出了在0.2、0.5、1.0 m/s速度条件下，Z=0平面上的气体流线图(X=-0.25～0.25 m)。由图6(a)发现在低速情况下(u=0.2 m/s)，每个电极上下游形成对称的四个涡。其中，上游涡比下游涡尺寸大，上游涡核靠近收集板，而下游涡核靠近放电极。在顺气流方向，对于电极上游的涡：涡尺寸越来越小，涡核越来越靠近收集板。对于电极下游的涡：第一个电极后的尺寸最大，第三个电极后次之，中间电极后的最小；第二个电极后的涡最靠近放电极，第三个次之，第一个最远。发现电极间的涡被压缩，形状更规则，接近圆形。由图6(b)可以看到，随着速度增加到0.5 m/s，下游的涡先消失，上游的涡移动并附在收集板上。

图6　不同速度下Z=0 m平面上的气体流线

图7给出了u=0.5 m/s 时，中心截面(Z=0 m)上的静压云图和速度云图。由图7(a)，静压分布与电势分布相似，整体呈环状，近电极处静压分布为环形。由图7(b)观察到：速度分布在第二、三个电极处形成两个对称的环分布，中间电极的分布更规则，成蝶状；近收集板处形成六个低速区域，对应图6(b)中的涡区域。

图7　当u=0.5 m/s时三电极电除尘器Z=0截面静压云图和速度云图

图8和图9分别给出了0.5 m/s时，有无EHD流条件下，截面X=-0.15、-0.10、-0.05、0、0.05、0.10、0.15 m上的速度云图。比较发现，EHD流的存在使得速度整体提高，近收集板的低速区范围扩大。从图8可以观察到：电极之间近上下壁面处，形成了环状的低速区域，这在图9中没有发现；中间电极截面上，壁面法向方向速度梯度(∂u/∂y)更低。

图8　EHD流下，X=-0.15、-0.10、-0.05、0、0.05、0.10、0.15 m截面速度云图(u=0.5 m/s)

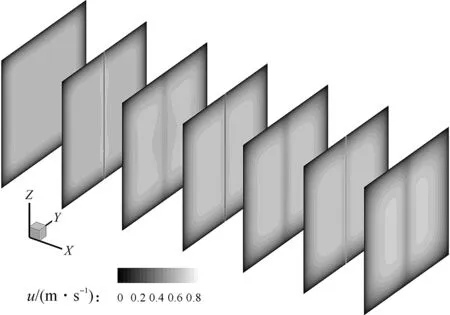
图9　无EHD流下，X=-0.15、-0.10、-0.05、0、0.05、0.10、0.15 m截面速度云图(u=0.5 m/s)

图10和图11分别给出了有EHD流情况下，上述7个截面的中心线(Z=0)上的速度分布和静压分布。从图10发现：EHD流使得放电极附近的速度明显增大，收集板附近的速度明显减小；电极间截面上，中心部分速度下降，速度分布整体呈M形。从图11可以发现，在三个放电极截面上，静压分布呈弧线形，与图4(h)中单电极的情况一致。而在非放电极截面上，静压分布曲线有一个小幅度的下凹，受EHD流影响较小。

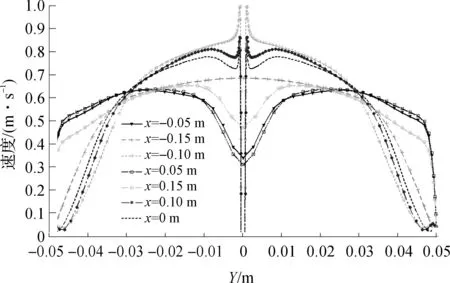
图10　EHD流下，X=-0.15、-0.10、-0.05、0、0.05、0.10、0.15 m截面中心线(Z=0)上的速度分布(u=0.5 m/s)

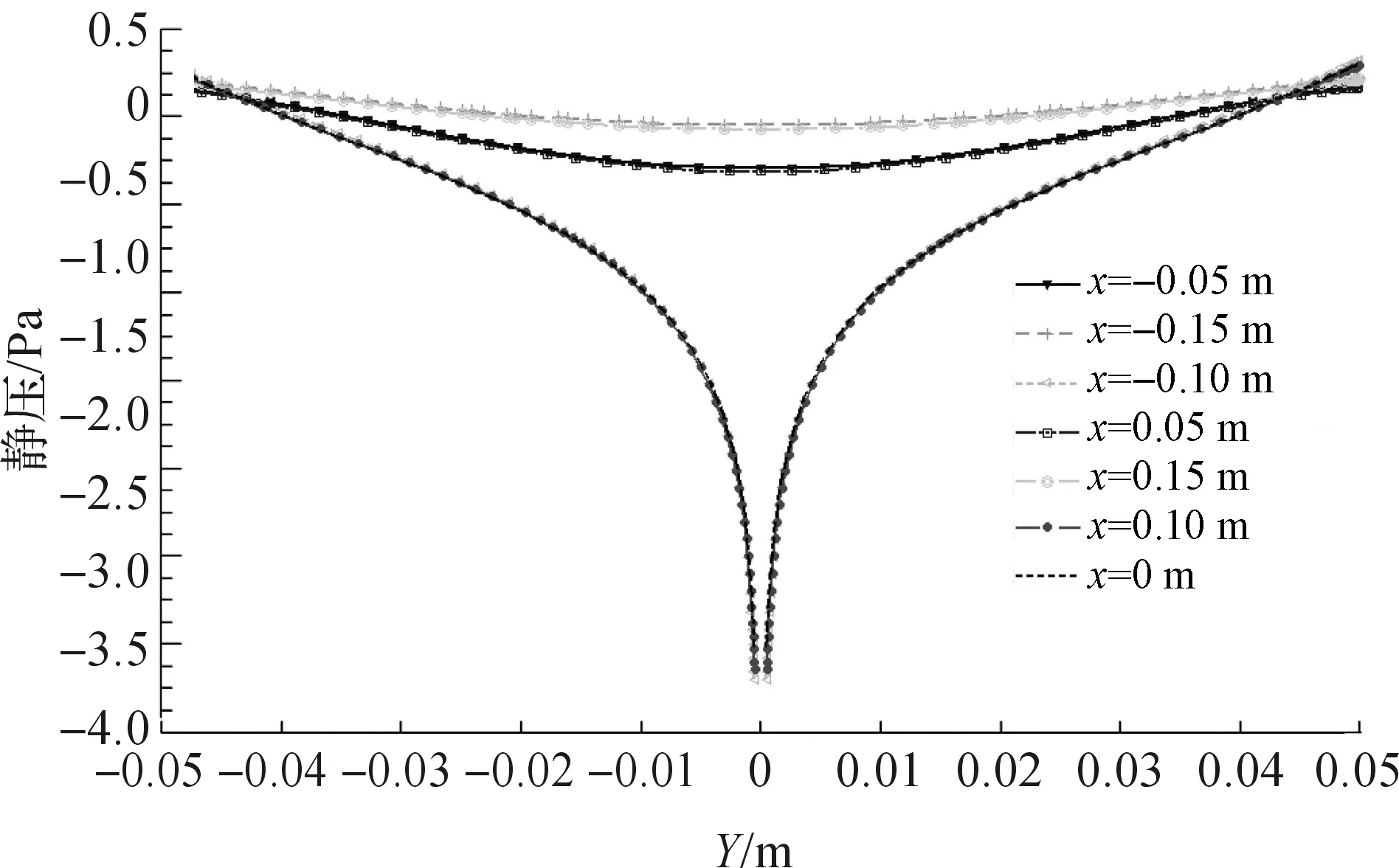
图11　EHD流下，X=-0.15、-0.10、-0.05、0、0.05、0.10、0.15 m截面中心线(Z=0)上的静压分布(u=0.5 m/s)

为了直观分析速度分布不均匀情况，以及静压分布对于气流运动的直接影响，图12给出了在有EHD流下，上述7个截面上的流线图。从图12(b)、(d)、(f)可以看到，前两个电极截面上的流线主要沿放电极表面向两边壁面法向方向，第三个电极截面上的流线则较为复杂。由图12(c)、(e)发现，在电极间截面上，流线主要沿收集板壁面法向方向，且流线的起始点集中在截面的上下壁面处，对应图8中上下壁面处的低速区域。随着X的增大，截面流线越来越复杂，流线型越来越紊乱，但中间电极截面(X=0m)上，流线却非常规则：靠近上下壁面中心处形成两个小涡，流线水平地沿着放电极向收集板。综合图5和图7中的电场、速度、静压分布，中间电极受到前后电极压力、速度、电势的挤压，因此中间电极处涡形状规则，规模削弱，速度分布均匀。

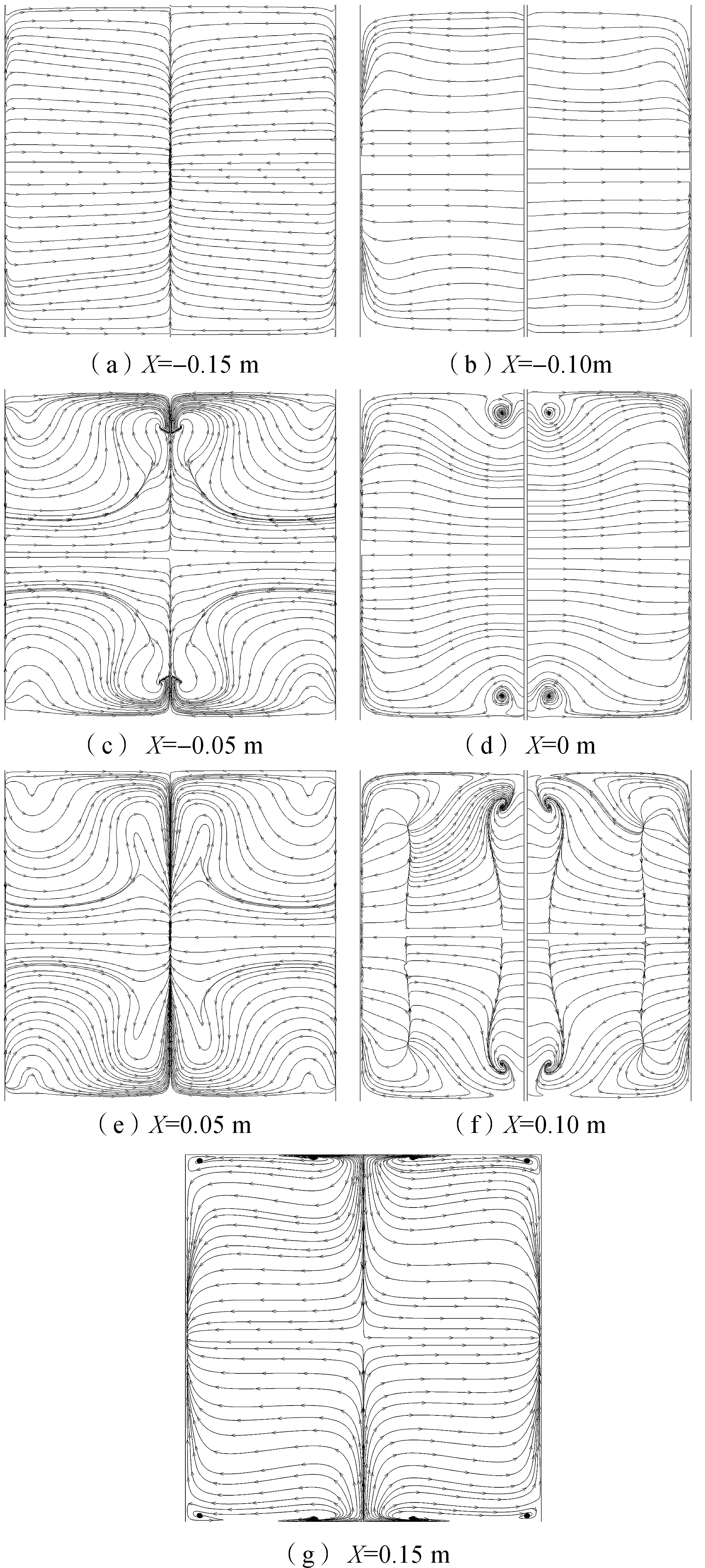
图12　EHD流下，X=-0.15、-0.10、-0.05、0、0.05、0.10、0.15 m截面流线图(u=0.5 m/s)

3　结　论

本文通过建立三维单电极和多电极电除尘器的几何与数值模型，对电除尘器内EHD流气动特性和极间干扰进了行分析，结论如下：

a)EHD流使得放电极上下游形成对称的四个涡，随着来流速度的增大，涡的尺寸减小，上游的涡核逐渐向收集板靠拢直到附在壁面上，下游的涡核向通道中心移动直至消失，下游涡比上游的涡先消失。

b)EHD流使靠近放电极处的速度增大，整体速度梯度提高，同时使两放电极连线中点处速度减小，沿Y方向呈“M”形。EHD的存在同时提高了湍流耗散率和湍动能的生成，两者综合考虑可以判断EHD流对湍流的影响。此外，EHD流使放电极截面上静压的水平分布变化为“V”形分布。

c)多电极电除尘器的电极间会产生极间干扰，电极周围电势的环形分布连成一片，而空间电荷密度分布区域被压缩，在两个放电极连线中点位置处，空间电荷密度几乎为零。同时，电极之间靠近上下壁面的位置，形成低速区。

d)在EHD流的影响下，中间电极受到前后电极的电场、速度、静压分布的影响，在前后电极的挤压作用下，中间电极处速度分布均匀，流线规则。同时，中间电极上下游涡的形状变得比较规则，但涡的区域变小。

[1]GUOBY,YANGSY,XINGM,etal.Towardthedevelopmentofanintegratedmultiscalemodelforelectrostaticprecipitation[J].IndustrialandEngineeringChemistryResearch,2013,52(33):11282-11293.

[2]LIUQ,ZHANGSS,CHENJP.Numericalanalysisofchargedparticlecollectioninwire-plateESP[J].JournalofElectrostatics,2015,74:56-65.

[3]ADAMIAKK.Numericalmodelsinsimulatingwire-plateelectrostaticprecipitators:areview[J].JournalofElectrostatic,2013,71:673-680.

[4]FARNOOSHN,ADAMIAKK,CASTLEGSP.Three-dimensionalanalysisofelectrohydrodynamicflowinaspikedelectrode-plateelectrostaticprecipitator[J].JournalofElectrostatics,2011,69(5):419-428.

[5]ZHAOL,ADAMIAKK.EffectsofEHDandexternalairflowsonelectriccoronadischargeinpin-plateconfiguration[C]// 2005IEEEIndustryApplicationsConference.HongKong:IAS,2005:2584-2589.

[6]PODLINSKIJ,NIEWULISA,MIZERACZYKJ,etal.ESPperformanceforvariousdustdensities[J].JournalofElectrostatic,2008,66(5/6):246-253

[7]CHANGJS,DEKOWSKIJ,PODLINSKIJ,etal.Electrohydrodynamicgasflowregimemapinawire-plateelectrostaticprecipitator[C]//2005IEEEIndustryApplicationsConference.IEEE,2005:2597-2600.

[8]LEONARDGL,MITCHNERAM,SELFSA.Anexperimentalstudyoftheelectrohydrodynamicflowinelectrostaticprecipitators[J].JournalofFluidMechanics,1983,127:123-140

[9]BOTTNERCU.Theroleofthespacechargedensityinparticulateprocessesintheexampleoftheelectrostaticprecipitator[J].PowderTechnology,2003,135/136:285-294.

[10]FARNOOSHN,ADAMIAKK,CASTLEGSP. 3-DnumericalanalysisofEHDturbulentflowandmono-dispersechargedparticletransportandcollectioninawire-plateESP[J].JournalofElectrostatics,2010,68(6):513-522.

[11]GAJBHIRAN,ESWARANV,SAHAAK,etal.Numericalcalculationofparticlecollectionefficiencyinanelectrostaticprecipitator[J].IndianAcademyofSciences,2015,40(3):863-873.

[12]AITSH,NOURIH,ZEBBOUDJY.Effectofairflowoncoronadischargeinwire-to-plateelectrostaticprecipitator[J].JournalofElectrostatics,2015,73:19-25.

[13]NIEWULISA,BERENDTA,PODLINSKIJ,etal.Electrohydrodynamicflowpatternsandcollectionefficiencyinnarrowwire-cylindertypeelectrostaticprecipitator[J].JournalofElectrostatics,2013,71(4):808-814.

[14]CHUDINOVAV,MARTYNOVICHYG,SULIMENKOVIV,etal.Studyofelectrosprayionmobilitydependenceontheionbunchdriftvelocityintheradiofrequencyquadrupole[J].JournalofAnalyticalChemistry,2014,69(13):1220-1228.

[15]WHITEFM.ViscousFluidFlow[M].Boston:McGrawHill,ThirdEdition,2006:62-64.

(责任编辑： 康锋)

Numerical Simulation Research on Electro-Hydrodynamics Flow and Interelectrode Interference of Electric Precipitator

ZHOUXiaoying,DOUHuashu,CHENXiaoping

(Faculty of Mechanical Engineering & Automation, Zhejiang Sci-Tech University, Hangzhou 310018, China)

3D numerical model was established for internal flow of single-electrode and multi- electrode electric precipitators, and the effects of electro-hydrodynamics (EHD) flow and interelectrode interference on internal flow characteristics of electric precipitators were studied. Poisson’s equation and electric current conservation equation were used to model the electric field, and the incompressible Navier-Stokes equation and standardk-εmodel were employed to describe the electric field distribution. Gas flow and electric field were worked out through coulomb force coupling. It is found that EHD flow makes the electrode form two symmetrical vortexes. With the increase in airflow inlet velocity, the two vortex cores moves to opposite directions. The EHD flow influences the turbulent intensity by both increasing the turbulent dissipation and production turbulent kinetic energy. The result depends on the dominant function. The results show that electrodes will generate interelectrode interference. Due to the squeezing action of potential and space charge distribution in the middle electrode, vortex strength reduces significantly, and the structure is more regular.

electric precipitator; collection efficiency; electrohydrodynamics; electric field force

10.3969/j.issn.1673-3851.2016.09.017

国家自然科学基金项目(51579224)

周小颖(1991-)，女，四川成都人，硕士研究生，主要从事流体机械方面的研究。

窦华书，E-mail: huashudou@yahoo.com

O442

A

1673- 3851 (2016) 05- 0734- 08 引用页码： 090404