基于极值分布的常态下高速公路行程时间可靠性模型
陈娇娜,张生瑞,靳引利2
(1.长安大学公路学院,西安 710064;2.长安大学电子与控制工程学院,西安 710064)
基于极值分布的常态下高速公路行程时间可靠性模型
陈娇娜1,张生瑞1,靳引利2
(1.长安大学公路学院,西安 710064;2.长安大学电子与控制工程学院,西安 710064)
为了利用参考模型表征路段行程时间分布,运用海量高速公路收费数据,分析了路段行程时间概率分布特征,通过极值分布、对数正态分布、正态分布和威伯尔分布对路段行程时间的概率密度函数进行曲线拟合.建立了基于极值分布的路段行程时间可靠性模型和模型参数估计方法,考虑了车型速度差和出行者易于理解的因素,提出了一种高速公路可靠性指标阈值的计算方法.选取最大概率行程时间、平均延误时间和行程时间可靠性为评价指标,对陕西省高速公路网中某一路段24 h出发车辆的行程时间进行实例评价.结果表明:极值分布的误差平方和(SSE)最小,拟合优度(R2)最接近于1,利用极值分布表征路段行程时间分布效果最佳.
交通工程;行程时间可靠性;概率密度函数;参数估计;极值分布
同一道路的行程时间可能会因出行时间不同而变化.行程时间可靠性是评价高速公路运行效率和服务水平的重要指标,决定了出行者对出发时间、路径和出行方式的选择.行程时间可靠性是微观出行决策的重要考虑因素[1],也是评价出行服务水平和道路运行效率的关键指标,对道路的管理者和使用者具有重要意义.高速公路行程时间可靠性能有效地衡量路网的不确定性,便于道路管理者准确评价路网运行状态以改善服务水平,同时有利于出行者在不完全掌握道路网交通状况条件下做出合理的出行决策.
研究人员从不同角度、针对不同研究对象、利用不同研究数据对行程时间可靠性进行了大量研究[2],研究了降雨[3-4]、雾天[5]、冰雪[6]、交通事故[7]等条件下对行程时间可靠性的影响,唐俊[8]、刘克[9]和王浩[10]分别使用浮动车数据、车检器数据和收费数据进行行程时间预测.出行者受到其性格、出行目的、对路网服务水平要求等因素影响,可接受的行程时间是不同的.孙小菲等[11]向北京市高速公路使用者调查其出行属性和可接受延误时间,由统计分析得知出行目的对可接受延误时间的影响不显著,仅私家车驾驶员平均可接受延误时间与平均行程时间基本正相关,对于大客车有所不同. Lida[12]认为以正态分布表示行程时间分布是可接受的.Bell和lida[13]认为,当交通量较大时,路径行程时间服从正态分布,交通量不大时,服从对数正态分布.Arezoumandi[14]分析伽马分布、最大极值分布、log-logistic概率分布、对数正态分布及威伯尔分布与18 h行程时间数据的拟合程度,得到可变限速情形下行程时间的分布服从对数正态分布.熊志华[15]根据路网波动状况以及路网用户的感知随机性,建立随机路网可靠性模型,得到晚高峰时段路段行程时间用Beta分布拟合效果较好的结论.李长城等[16]考虑了客车与货车间速度差异明显,利用高速公路收费数据对路段行程时间概率分布进行拟合,结果表明正态分布相较于威伯尔分布和伽马分布具有更好的拟合效果.李小静等[17]基于日变可靠度并假设行程时间及其规定阈值服从正态分布,分析了可靠度影响因素.陈琨等[18]使用北京市浮动车数据,分别用正态分布、对数正态分布、伽马分布和威伯尔分布对路段行程时间的概率密度函数进行了曲线拟合,结果表明对数正态分布的拟合效果最佳,分别考虑路段相关和路段独立2种情况,建立了基于对数正态分布的路径行程时间可靠性评价模型.陈小鸿等[19]针对正态分布或对数分布不能有效地描述小间隔行程时间分布的问题,提出基于浮动车数据的行程时间经验分布,得到了以15 min为间隔的不同出发时段行程时间的可靠度指标.尹志鹏等[20]基于对数正态分布,采用标准差、缓冲指数和拥挤频率来评价旅行时间可靠性.从国内外已有研究来看,行程时间可靠性计算方法及评价体系研究不断深入,但对于行程时间分布尚未形成统一结论.
高速公路收费数据包含了入口站编号、出口站编号、入口日期及时间、出口日期及时间、车型、车种、车辆牌照等信息[21],可以较为准确地计算路网中车辆的实际行程时间.本文利用陕西省高速公路收费数据,选取误差平方和(SSE)和拟合优度(R2)作为衡量指标,在无突发事件条件下,分析极大值分布、对数正态分布、正态分布和威伯尔分布与行程时间历史概率密度的拟合程度.从道路使用者的角度提出一种确定可接受行程时间阈值的方法,建立高速公路行程时间可靠性模型,并验证模型的有效性和适用性.
1 高速公路行程时间分布的统计拟合
1.1行程时间可靠性定义
高速公路行程时间可靠性是指在高速公路上给定的起讫点(origin destination,OD)之间,出行者能在规定时间内顺利完成出行的概率[22].由文献[18]可知,路网中路段单元的行程时间可靠性模型可以描述为
式中:Ri,L表示在服务水平L下路段I行程时间可靠度;ti为一个随机变量,表示路段I的实际行程时间;Ti,L表示在服务水平L下路段I行程时间的阈值.求解路段行程时间可靠性的问题,实际上就是求解路段行程时间的累积分布函数.
1.2数据筛选
1.2.1数据来源
高速公路运输通常是长距离出行,因此,交叉口以及收费站所产生的延误相对总的行程时间而言可忽略不计.同一条记录下的出站时间与进站时间之差则为该记录对应车辆的行程时间.计算公式为
式中:t为行程时间;tout为出口日期及时间;tin为入口日期及时间.
1.2.2筛选有效样本数据
剔除由于收费系统故障、人工操作失误、特殊驾驶事件等产生的异常数据.由于重大节假日免收小型客车通行费,交通需求波动明显.为避免重大节假日对分析结果造成偏差,需要剔除重大节假日期间(春节、清明、劳动节、国庆节)的数据.
常态下,绝大多数相同时间段内起讫点相同的车辆行驶特征是相似的,具有相似的行程时间.依据统计学原理,样本均值的上下2个标准差范围内包含一个样本中绝大多数的数据,能准确地反映该时段内出发的车辆行程时间的一般特征.选取该范围内数据为有效样本数据,筛选流程如图1所示.
1.2.3车型分类
在高速公路联网收费系统中根据收费标准的不同,利用vehicletype和vehicleclass车型编码字段,将收费车型划分为9类(客车4类,货车5类).为得到较好的拟合模型,消除不同车型的设计速度或限速值的影响,采用交通调查的车型分类标准,将样本车辆类型分为6类(客车2类,货车4类).收费车型编码字段与交调车型对应情况详见表1.

表1 收费车型编码字段与交调车型对应情况Table 1 Classification of vehicle type in traffic survey
1.3拟合结果衡量指标
t1,…,tn表示随机样本Tv(v=1,…,6)的观测值,t(1)≤…≤t(i)≤…≤t(n)是次序统计量,Fi(t)为相应t(i)的频率,则样本经验分布函数为
式中k表示{t1,…,tn}中等于t(i)的个数,i=1,…,n.
分布拟合效果采用误差平方和(SSE)和拟合优度(R2)来衡量.SSE用于反映拟合估计值与样本的接近程度,R2用于说明曲线拟合在解释数据的变异性方面是否成功,样本的分布特征是否得到保留.
SSE表示拟合数据和原始数据对应点的误差的平方和.SSE越接近0,则曲线的拟合效果越好.
拟合优度R2取值范围为[0 1],值越接近1,曲线拟合的效果越好.计算如下:
式中:pi表示原始数据中行程时间ti的经验概率值;p^i表示拟合分布中行程时间ti的概率估计值;表示原始数据经验分布概率的均值.
1.4分布统计拟合
采用陕西省2015年上半年(1月—6月)高速公路收费数据作为基础数据,并剔除春节、清明、劳动节期间的数据.根据车型和出发时间(以1 h为间隔)将样本分为6×24组.样本容量为1×105,对每组样本进行随机抽样.通过极大值分布、对数正态分布、正态分布和威伯尔分布对各组单位距离行程时间的概率密度函数进行曲线拟合,并计算拟合效果评价指标SSE和R2.
6×24组样本的拟合指标计算结果用箱型图表示,如图2和图3所示.由图2可知,与其他分布相比,极大值分布的SSE在一个稳定且较小的水平.由图3可知,极大值分布的R2最接近于1,说明极大值分布能很好地拟合数据的变异性.对6类车型在不同出发时段的样本进行分布拟合,结果表明:极大值分布的SSE最小且R2最大,说明极大值分布在拟合某个行程时间的概率时效果最优.
利用假设检验方法,在显著性水平为0.05的条件下,对路段行程时间是否符合极大值分布进行了检验,结果表明:利用极大值分布拟合行程时间分布的概率密度函数是可接受的,拟合结果指标均优于对数正态分布、正态分布和威伯尔分布.
2 高速公路行程时间可靠性评价
2.1行程时间可靠性模型
由1.4节统计分析结果可知,路段行程时间服从极大值分布.因此,路段行程时间的概率密度函数可以由极大值分布模型
来描述.式中:α>0;-∞<μ<+∞;ti为路段I的行程时间.μ和α为待定系数,μ为分布的位置参数,α为分布的尺度参数.由概率密度函数可以得到路段行程时间的概率分布函数,即路段行程时间可靠性模型
式中Ti,L为路段行程时间阈值.
路段行程时间可靠性模型求解的关键是标定路段行程时间的μ和α这2个参数.
2.2极值分布的参数估计方法
极值分布常用参数估计方法有矩法、耿贝尔法、极大似然法和概率权值法,均能给出满意的参数估计结果[23].在统计学理论上,极大似然估计是一种较优的参数估计方法[24],本文采用最大似然估计法求解这2个参数.
当观测数据t1,…,tn给定时,构造似然函数L并取对数,得
分别对μ和α求导并令其为0,得
采用迭代法求解μ和α.
2.3行程时间阈值
对于出行者而言,在没有天气、特殊事件等偶发因素的情况下,关注最大可能的行程时间,即期望行程时间等于某一时段内路段上的行程时间众数.即
式中:EI(ti)为期望行程时间,即概率密度函数中发生概率最大的行程时间;Δti为可接受的延误时间;φ为期望行程时间的系数,常取5%、10%、15%或20%.根据不同的研究目标选择系数φ.
2.4行程时间可靠性评价
采用最大概率行程时间Tpmax、平均延误时间Ta和行程时间可靠性R三个指标来评价行程时间的可靠性.
最大概率行程时间Tpmax即高速公路用户行程时间的众数,能够最直观地反映常态下路网运行状态,可以作为辅助判断路网运行异常的参考数据,也是行程时间预测的重要指标.
平均延误时间Ta可以反映交通延误的影响范围和影响程度.给定样本有序序列为t1≤…≤tk-1≤tk≤tk+1≤1…≤tn,tk-1≤Ti,L≤tk,则计算公式为
式中:Td表示累计延误时间;Ti,L表示期望的行程时间,计算见式(10).
行程时间可靠性R可以反映路网运行状态的稳定性或波动性.根据行程时间可靠性模型和时间阈值的定义可得
3 实例分析
选取2015年7月陕西省高速公路一个路段进行可靠性分析,该路段全长18.2 km.通过Tpmax能够获得一般情况下该路段上行驶车辆的最大概率运行速度v,分别计算不同车型的Tpmax和v,如表2所示.由表2可知,S-Car的Tpmax明显小于其他车型,且与L-Car有显著差异;S-Truck、M-Truck、L-Truck和EL-Truck的Tpmax波动范围较小.说明该路段客车中S-Car的运行速度较高,4种类型货车的运行速度相似.

表2 6类车型的最大概率行程时间Tpmax及相应的速度vTable 2 Tpmaxand v of each vehicle type
以φ=10%确定各类车型的期望行程时间,计算一天二十四小时内不同时段的R和平均延误时间Ta,如表3所示.各时段行程时间可靠性R如图4所示.

表3 各时段行程时间可靠性指标R和平均延误时间TaTable 3 Indexes of R and Tain each period
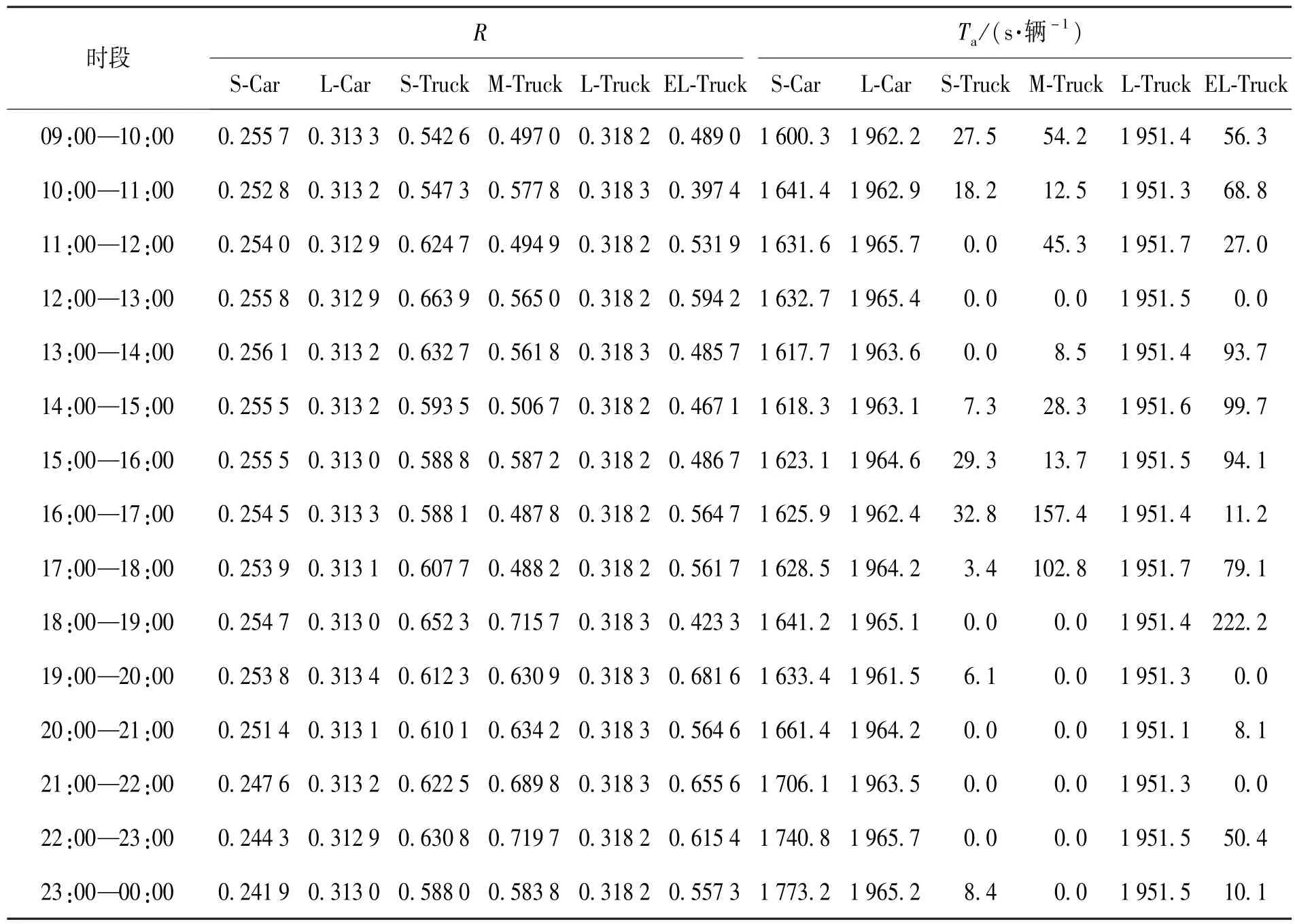
续表
由图4可知,货车的R均高于客车,S-Truck尤为显著.L-Car和L-Truck的R相近,且不受出发时段的影响.S-Truck、M-Truck和EL-Truck的R受出发时段的影响较为显著.其中,S-Truck在06:00—08:00时段内,R略有降低;M-Truck和EL-Truck在04:00—06:00时段内,R显著降低.说明在04:00—06:00时段内是M-Truck和EL-Truck集中出行的高峰,该时段道路可靠性指标比其他时段差,该时段内道路最有可能出现拥挤状况.
由表5中Ta可知,L-Car和L-Truck的平均延误时间最高,且波动较小,说明该路段L-Car和LTruck在每次出行中几乎都在承受一定程度的延误.该路段S-Truck、M-Truck和EL-Truck在早晚高峰受到轻微程度的延误,即08:00—11:00和15:00—17:00.
通过分析6种车型的Tpmax、Ta和R在一天不同时段的分布,结果表明:客车的行程时间可靠性较货车低,且不受出发时段的影响,各个时段的Ta超过1 600 s/辆,即该路段的交通延误已近趋近于常态,需要管理者采取相应的管理措施.
4 结论
1)通过极大值分布、对数正态分布、正态分布和威伯尔分布对高速公路网中单位距离行程时间的概率密度函数进行曲线拟合,极大值分布的SSE最小,R2最接近于1.说明利用极值分布表征路段行程时间分布效果最佳.
2)给出了基于最大概率行程时间的可接受行程时间阈值,建立了高速公路路段行程时间的可靠性模型.选取Tpmax、Ta、R作为行程时间可靠性评价的指标,对陕西省高速公路网进行实例分析.结果表明:基于极大值分布的路段行程时间可靠性模型能够准确地反映道路运行的稳定性,更容易判别和比较道路真实交通状况.
3)对于突发事件情况下或具有特殊构造物的路段行程时间可靠性需要进一步考虑.
[1]侯立文,谭家美.信息条件下路段出行时间可靠性的计算[J].上海交通大学学报,2006,40(6):968-972. HOU L W,TAN J M.Computing the link travel time reliability with information provision[J].Journal of Shanghai Jiaotong University,2006,40(6):968-972. (in Chinese)
[2]柏喜红,陈旭梅,王莹,等.高速公路行程时间可靠性研究综述[J].交通运输工程与信息学报,2014,12 (2):70-76. BAI X H,CHEN X M,WANG Y,et al.Review on travel time reliability research of freeways[J].Journal of Transportation Engineering and Information,2014,12 (2):70-76.(in Chinese)
[3]王婧,何杰,吴炼.雨天高速公路网行程时间可靠性评价方法[J].交通运输系统工程与信息,2011,11(6): 117-123. WANG J,HE J,WU L.Evaluation approach of travel time reliability for highway network under rain[J]. JournalofTransportationSystemsEngineeringand Information Technology,2011,11(6):117-123.(in Chinese)
[4]叶佳缘,杨赛霓,刘浩.降雨对高速公路小型车行程时间的影响[J].公路交通科技,2012,29(11):135-139,158. YE J Y,YANG S N,LIU H.Impact of rainfall on freeway travel time for passenger cars[J].Journal of Highway and TransportationResearchandDevelopment,2012,29 (11):135-139,158.(in Chinese)
[5]吴炼,李旭宏,王婧,等.雾天高速公路网行程时间可靠性评价方法[J].解放军理工大学学报(自然科学版),2010,11(2):233-238. WU L,LI X H,WANG J,et al.Reliability evaluation on travel time in freeway network under fog environment influence[J].Journal of PLA University of Science and Technology(Natural Science Edition),2010,11(2): 233-238.(in Chinese)
[6]冷军强.冰雪条件下城市路网行程时间可靠性研究[D].哈尔滨:哈尔滨工业大学,2010. LENG J Q.Travel time reliability of urban road network under ice and snowfall conditions[D].Harbin:Harbin Institute of Technology,2010.(in Chinese)
[7]陈玲娟,刘海旭,蒲云.交通事故持续期内行程时间的可靠性研究[J].西南交通大学学报,2013,48(2): 376-382. CHEN L J,LIU H X,PU Y.Travel time reliability during incident duration time[J].Journal of Southwest Jiaotong University,2013,48(2):376-382.(in Chinese)
[8]唐俊.基于浮动车数据的高速公路路段行程时间预测方法研究及系统实现[D].广州:中山大学,2011. TANG J.Freeway link travel time prediction research and system implementation based on float car data[D]. Guangzhou:Zhongshan University,2011.(in Chinese)
[9]刘克.高速公路的路段行程时间估计与预测方法研究[D].北京:北京交通大学,2013. LIU K.Estimation prediction of link travel time for freeways[D].Beijing:Beijing Jiaotong University,2013. (in Chinese)
[10]王浩.基于收费数据的高速公路旅行时间自适应插值卡尔曼滤波预测研究[D].北京:北京交通大学,2014. WANG H.Highway travel time prediction research based on adaptive interpolation Kalman filter and toll collection data[D].Beijing:Beijing Jiaotong University,2014. (in Chinese)
[11]孙小菲,陈旭梅,刘文峰,等.高速公路行程时间可靠性评价体系及指标阈值标定[J].交通信息与安全,2014,32(1):58-63. SUN X F,CHEN X M,LIU W F,et al.Development of an evaluation system of the reliability of travel time of freeways and the threshold of corresponding indicators [J].Journal of Traffic Information and Safety,2014,32 (1):58-63.(in Chinese)
[12]LIDA Y.Basic concepts and future directions of road network reliability analysis[J].Journal of Advanced Transportation,1999,33(2):125-134.
[13]BELL M G H,LIDA Y.Transportation network analysis [M].New York:John Wiley&Sons,1997.
[14]AREZOUMANDI M.Estimation of travel time reliability for freeways using mean and standard deviation of travel time[J].Journal of Transportation Systems Engineering and Information Technology,2011,11(6):74-84.
[15]熊志华.道路网行程时间可靠性基础理论与方法研究[D].北京:北京交通大学,2006. XIONG Z H.Study on theory and method of travel time reliability about road network[D].Beijing:Journal of Beijing Jiaotong University,2006.(in Chinese)
[16]李长城,文涛,刘小明,等.基于高速公路收费数据的行程时间可靠性模型研究[J].公路交通科技,2014,31(12):110-115.LI C C,WEN T,LIU X M,et al.Study on reliability model of travel time based on expressway toll data[J]. Journal of Highway and Transportation Research and Development,2014,31(12):110-115.(in Chinese)
[17]李小静,牟海波,杨菊花.基于道路使用者的城市路网动态行程时间可靠度[J].公路交通科技,2014,31 (4):106-113. LI X J,MOU H B,YANG J H.Dynamic travel time reliability of urban road network based on road users[J]. Journal of Highway and Transportation Research and Development,2014,31(4):106-113.(in Chinese)
[18]陈琨,于雷.基于对数正态和分布的路径行程时间可靠性模型[J].北京交通大学学报,2009,33(3):35-39. CHEN K,YU L.Route travel time reliability model based on lognormal sum distribution[J].Journal of Beijing Jiaotong University,2009,33(3):35-39.(in Chinese)
[19]陈小鸿,冯均佳,杨超.基于浮动车数据的行程时间可靠度特征研究[J].城市交通,2007,5(5):42-45,37. CHEN X H,FENG J J,YANG C.Research on travel time reliability characteristics based on floating car data [J].Urban Transport of China,2007,5(5):42-45,37.(in Chinese)
[20]尹志鹏,刘伟铭,庄岩浩.基于高速公路收费数据的旅行时间可靠性分析[J].公路与汽运,2014(164): 52-57. YIN Z P,LIU W M,ZHUANG Y H.Analysis on travel time reliability based on the data of the expressway toll [J].Highways&Automotive Applications,2014(164): 52-57.(in Chinese)
[21]庄岩浩.基于收费数据的高速公路旅行时间可靠性分析与应用[D].广州:华南理工大学,2014. ZHUANG Y H.Travel time reliability analysis and applicationbasedonthehighwaytolldata[D]. Guangzhou:South China University of Technology,2014. (in Chinese)
[22]Federal Highway Administration.Traffic congestion and reliability:trends and advanced strategies for congestion Mitigation[R/OL].[2005-11-10].http:∥ops.fhwa. dot.gov/congestion_report/chapter2.htm.
[23]段忠东,周道成.极值概率分布参数估计方法的比较研究[J].哈尔滨工业大学学报,2004,36(12): 1605-1609. DUAN Z D,ZHOU D C.A comparative study on parameter estimate method for extremal value distribution [J].Journal of Harbin Institute of Technology,2004,36 (12):1605-1609.(in Chinese)
[24]黄浩辉,宋丽莉,植石群,等.广东省风速极值I型分布参数估计方法的比较[J].气象,2007,33(3): 101-106. HUANG H H,SONG L L,ZHI S Q,et al.Comparison ofestimationofwindspeedextreme-Idistribution parameters in Guangdong province[J].Meteorological Monthly,2007,33(3):101-106.(in Chinese)
(责任编辑 梁 洁)
Expressway Travel Time Reliability Model Without Incident Based on the Extreme Value Distribution
CHEN Jiaona1,ZHANG Shengrui1,JIN Yinli2
(1.School of Highway,Chang'an University,Xi'an 710064,China;2.School of Electrical and Control Engineering,Chang'an University,Xi'an 710064,China)
Massive historical data of the expressway toll was collected and fitted by several distributions,including extreme value,log-normal,normal and Weibull.Travel time reliability model was established based on the extreme value distribution,and a parameter estimation method was provided.To be understood by travelers easily,the threshold was also built considering the difference between cars and trucks.Three indexes were selected as the evaluation index,including the maximum probability travel time,the average delay time and travel time reliability.The proposed model was validated by the case study of Shaanxi.Based on the principles of the less error sum squares(SSE)and the higher determination coefficient(R2),the results show that it is rational and acceptable to describe the travel time with the extreme value distribution.
traffic engineering;travel time reliability;probability density function;parameter estimation;extreme value distribution
U 491.2;TP 391
A
0254-0037(2016)09-1398-08
10.11936/bjutxb2015110020
2015-11-06
陕西省科技攻关项目(2012k06137);陕西省交通运输厅科研项目(14-40X)
陈娇娜(1989—),女,博士研究生,主要从事交通运输规划与管理方面的研究,E-mail:chenjiaona2015@163.com
张生瑞(1963—),男,教授,主要从事交通运输规划与管理方面的研究,E-mail:zhangsr@chd.edu.cn

