基于统计及结构稀疏特性的图像修复算法

于文静　毕东旭　颜学峰　林家骏

(华东理工大学信息学院　上海 200237)



基于统计及结构稀疏特性的图像修复算法

于文静毕东旭颜学峰*林家骏

(华东理工大学信息学院上海 200237)

目前普遍使用的基于等照度线的优先权图像修复算法，不能快速准确地确定待修复图像的结构位置。提出利用破损区域边缘图像块的灰度均值直方图，快速准确定位结构点的位置，优先修复结构区域后，实现纹理区域修复，获得很好的修复结果。该算法与传统算法相比，不必计算每个边缘图像块的优先级，直接利用统计信息获得结构点的位置，比传统算法更准确获取结构点位置。算法的计算效率和修复效果都有了很大提升。

图像修复灰度均值直方图结构稀疏

0　引　言

图像修复[1]是利用已知信息估计未知信息，从而将破损的图像修补完整，使其平滑、连续、符合人眼的视觉要求。随着图像修复在数字特效、图像恢复和图像编码、传输等方面的广泛应用，图像修复正在成为图像处理研究中的基础领域。

目前常用的图像修复方法可以分为基于扩散的方法，基于样本的方法。基于扩散的方法[1-3]是利用待修补区域的边缘信息确定扩散信息和扩散方向，从区域的边界各向异性地向边界内扩散，这些算法通过变分法或高阶的偏微分方程实现。基于扩散的算法在处理非纹理图像和破损区域较小的图像修复中取得了较好的效果。基于样本的图像修复方法[4-6]是在已知区域中寻找最匹配的图像块，对于未知区域进行填充。这一方法最早由Efros等[7]提出的利用从已知区域采样最为匹配的图像块来合成未知区域的信息。Criminsi等[4]提出了一种基于图像块的图像修复算法，对于破损区域综合地考虑结构和纹理的特征，算法实现了部分图像从结构区域首先去修复，取得了很好的效果。近年来，稀疏表达开始应用于图像修复[8-11]，其基本思想是用稀疏的组合来表达图像块的信息。基于样本的图像修复算法对图像进行修复时需要计算破损区域边缘图像块的优先级以保证位于结构的区域首先被修复，这既增加了计算的冗余而且在结构区域复杂的图像中不能准确确定结构点的位置。本文提出基于统计及结构稀疏特性的图像修复算法，利用破损区域边缘邻域的图像块的灰度均值的统计确定结构稀疏点的位置，能准确获取图像结构点的位置，并快速修复结构区域。在修复速度和效率上获得较好结果。

1　Criminisi算法的实现

Criminisi算法[4]主要通过以下三步来完成。

(1) 确定修复优先权

定义位于破损区域边界∂Ω的点p为中心的待修复块Ψp，其修复优先权P(p)：

P(p)=C(p)D(p)

(1)

其中，C(p)是置信度表示在Ψp中已知信息所占的比例，D(p)是待修复块Ψp的数据项。

(2)

(3)

其中：

(4)

(5)

(3) 置信度的更新

每完成一次填充修复，新填入像素p′的置信度更新为：

C(p)=C(p′),∀p∈Ψp′∩Ω

(6)

重复(1)、(2)、(3)直到修复完成。

2　基于统计的结构稀疏特性算法的实现

在Criminisi算法中，每修复一块图像块，即要对边缘所有点进行优先权的计算，而且在图像纹理区域具有颜色变化时，会产生纹理修复过渡扩展的现象。

自然图像的结构相比纹理具有更高的稀疏度，处于图像结构位置的图像块与邻域的图像块的相似性具有更高的稀疏度。利用图像的这一特征，提出利用结构稀疏性的特征，统计破损区域邻域信息，获取结构点位置，并从结构点位置开始进行修复。不必计算每个点的修复优先权，既能准确获取结构点的位置，并能鲁棒性地修复结构信息。算法实现步骤如下。

(1) 破损区域邻域图像块灰度均值获取

如图1所示，沿着∂Ω以边缘的P点为中心点计算每个待修复块Ψp中已知像素的平均灰度值。算法中图像块的大小设为3×3。图中红色区域为破损区域。

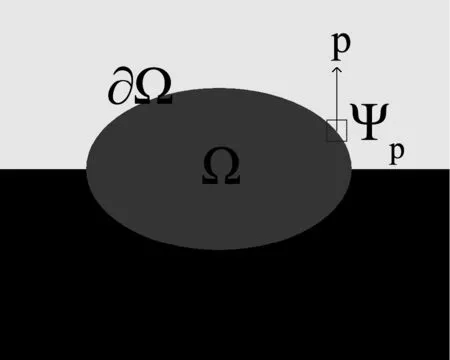
图1　原理图

(7)

(2) 灰度值统计直方图的建立

(8)

图2　邻域灰度统计直方图

(3) 破损区域结构位置的获取

利用直方图灰度数量较少的点，如图2中灰度值均值分别为0.4和0.6是图像中的稀疏点，其在图像中的位置如图3中标识A、B点。算法确定这两点的位置为结构位置，从这些点开始对破损图像进行修复。修复过程块的匹配利用在特定邻域中图像块的匹配算法，如文献[8]算法中图像块的匹配方法。

图3　结构点位置

利用图像灰度均值直方图确定结构位置时，会出现某些邻域灰度均值的数量较少但是不位于结构位置，但是通过迭代后这些点会消失，稀疏点的位置会回归到结构位置。

(4) 修复迭代至结构稀疏点消失

每修复一个图像块，对于改变后的边缘直方图信息进行更新，只需重新计算增加的边缘信息，重新回到(1)。直到直方图中结构稀疏点的消失，即结构区域已修复完成。如图4为利用本算法修复结构后的图像。

图4　结构修复完成

(5) 沿着破损区域方向修复纹理区域

确定结构区域修复结束后，沿着破损区域直接在邻域中进行块的匹配和修复即可获得。纹理区域的修复，只在结构位置两侧分别进行图像块的匹配，在保证修复质量的同时节省修复时间。

3　实验结果与分析

利用本算法对BSDS300图像数据库中的多幅图像进行处理，并运用Criminisi算法和本算法进行比较，结果表明本算法的修复效果比较好。另外，为了定量比较算法的修复效果，采用峰值信噪比(PSNR)和算法运行时间作为比较的评价标准。

实验1中物体移除过程中，如图5所示，由于Criminisi算法在修复过程中对于最先修复点的依赖性大，而且在迭代过程中误差的积累使得修复的结果中出现将错误区域的信息匹配到填充区域。本算法利用邻域统计，计算破损区域边缘的每个点的3×3邻域图像块的平均灰度值，利用灰度值建立边缘的灰度信息直方图，准确获得破损区域结构位置，首先修复结构区域。所以修复结果中结构区域更自然。

图5　实验1

实验2在修复破损区域时，如图6所示，在其邻域存在结构的变化，Criminisi算法在修复过程中随着迭代次数的增加，置信度下降，使修复结果出现结构的不连续。本算法在修复结构后利用邻域信息匹配为填充区域，获得满意的结果。

图6　实验2

表1给出了实验1和实验2利用Criminisi算法与本算法进行处理后PSNR值的对比。本算法修复的结果在2个实验中PSNR与Criminisi算法近似。在计算时间上，实验1和实验2对于破损区域修复，本算法修复时间是Criminisi算法所用时间的50%。对于BSDS300图像库中的50幅图像，对于不同面积的破损区域(大小从20×20～70×70)的图像进行修复两种算法进行比较，本算法的修复时间平均为Criminisi算法的50%。

表1　图像修复性能的比较

4　结　语

本文算法首次将统计直方图应用于结构位置的确定，使修复算法在无需对边缘每个像素点进行优先级的复杂计算的条件下，快速准确地确定结构位置。算法充分利用自然图像稀疏性先验的特征，通过计算图像块的平均灰度，利用信息分布的稀疏性，简便，有效。算法可以准确地确定区域中是否存在结构区域，在纯纹理区域及结构和纹理区域混杂的图像中，自适应地对图像进行修复，获得较好效果。

本文算法不能很好处理破损区域中同时含有多种结构信息的图像，这一问题是要进一步研究解决的。

[1]BertalmioM,SapiroG,CasellesV,etal.Imageinpainting[J].ACMTransactiononGraphics,2000,19(3):417-424.

[2]ChanT,OsherS,ShenJ.TotalvariationdenoisingandenhancementofcolorimagesbasedontheCBandHSVcolormodels[J].JournalofVisualCommunicationandImageRepresentation,2001,12(4):422-435.

[3]BertalmioM,BertozziAL,SapiroG.Navier-Strokes,fluiddynamics,andimageandvideoinpainting[C]//ProceedingsofIEEEComputerSocietyConferenceonComputerVisionandPatternRecognition,2001:417-424.

[4]CriminisiA,PerezP,ToyamaK.Objectremovalbyexamplar-basedimageinpainting[C]//ProceedingsofInternationalConfereceonComputerVision,2003:721-728.

[5]WuJ,RuanQQ.Objectremovalbycrossisophotesexamplar-basedimageinpainting[C]//ProceedingsofInternationalConferenceonPatternRecognition,2006:810-813.

[6]WongA,OrchardJ.Anonlocal-meansapproachtoexamplar-basedinpainting[C]//ProceedingsofIEEEInternationalConferenceonImageProcessing,2008:2600-2603.

[7]EfrosA,LeungT.Texturesynthesisbynon-parametricsampling[C]//ProceedingsofInternationalConferenceonComputerVision,1999:1033-1038.

[8]XuZB,SunJ.Imageinpaintingbypatchpropagationusingpatchsparsity[J].IEEETransactionsonImageProcessing,2010,19(5):1153-1165.

[9]ZhangQ,LiJJ.Examplar-basedimageinpaintingusingcolordistributionanalysis[J].JournalofInformationofScienceandEngineering,2012,28(4):641-654.

[10]EladM,StarckJL,QuerreP,etal.Simultaneouscartoonandtextureimageinpaintingusingmorphologicalcomponentanalysis[J].AppliedandComputationalHarmonicAnalysis,2005,19:340-358.

[11]GuleryuzOG.Nonlinearapproximationbasedimagerecoveryusingadaptivesparsereconstructions[C]//ProceedingsofIEEEInternationalConferenceonImageProcessing,2003:713-716.

IMAGEINPAINTINGALGORITHMBASEDONSTATISTICSANDSTRUCTURESPARSITYCHARACTER

YuWenjingBiDongxuYanXuefeng*LinJiajun

(School of Information,East China University of Science and Technology,Shanghai 200237,China)

Currentpopularimageinpaintingalgorithmisbasedonisophotepriority,whichcannotdeterminethestructurelocationoftheimagetoberestoredfastandaccurately.Ouralgorithmsuggeststousegray-meanhistogramofthepatchonrimofthedeterioratedregiontorapidlypositionthelocationofstructurepoints,andafterapriorinpaintingonstructureregion,thefilling-inoftextureregionwillbeimplemented.Thisachievesverygoodrestoringresult.Comparingouralgorithmwiththeclassicalalgorithm,itdoesnotneedtocalculatetheprioritiesofeveryedgepatchbutdirectlymakesuseofstatisticsinformationtoobtainthelocationofstructurepoints,andismoreaccuratethanacquiredbytraditionalalgorithm.Boththecomputationefficiencyandinpaintingeffectofthisalgorithmaregreatlyimproved.

ImageinpaintingGray-meanhistogramStructuresparsity

2015-05-20。于文静，讲师，主研领域：数字图像修复算法及优化算法。毕东旭，硕士。颜学峰，教授。林家骏，教授。

TP391.41

ADOI:10.3969/j.issn.1000-386x.2016.03.049