基于蚁群算法的直升机舰面系留索预紧力优化

吴　靖　胡国才

1(海军航空工程学院研究生管理大队　山东 烟台 264001)2(海军航空工程学院飞行器工程系　山东 烟台 264001)



基于蚁群算法的直升机舰面系留索预紧力优化

吴靖1胡国才2

1(海军航空工程学院研究生管理大队山东 烟台 264001)2(海军航空工程学院飞行器工程系山东 烟台 264001)

根据直升机在舰面系留时的受力情况，提出一种以直升机6个刚体位移为变量的系留载荷计算方法。针对系留索预紧力优化属于多变量连续空间优化这一特点，采用嵌入确定性搜索的连续域蚁群算法对系留索预紧力进行优化，并在算法中加入MMAS策略，防止算法过早陷入局部最优解。结果表明，该蚁群算法经过二十多步迭代后能够使目标值稳定地收敛，较好地解决了直升机系留索预紧力优化问题。最后，对某型直升机无预紧力和预紧力优化后的系留载荷进行对比分析，无预紧力时多条索具持续松弛未起到系留作用，而预紧力优化后系留索最大张力降低了35.02%，且索具张力分布更均匀。

直升机系留预紧力蚁群算法优化

0　引　言

由于舰船的运动，直升机在甲板或机库停放时会产生移动、翻转等不稳定现象。特别是在高海情下，可能导致机体受损，为了保证直升机停放的安全，必须要有可靠的系留索具将其固定于甲板或机库。海情不同或停放位置不同，舰载直升机的系留方案也不同，最好的系留方案必须使系留索和机体系留点产生的载荷最小，这样才能增加直升机的结构强度延长直升机的使用寿命。

确定系留方案前提是要有准确的系留载荷计算模型，孙淑苓等[1]运用矩阵力法和位移法对系留载荷进行了计算；李进军等[2]采用能量法对系留载荷进行计算，并采用筛选法和逐步调整的试算法对甲板系留点位置进行了优化；金海波等[3]对考虑轮胎变形的系留计算模型进行了研究，表明轮胎的压缩变形会使系留载荷增加；李书等[4]采用遗传算法对甲板系留点位置进行了优化；吴靖等[5]以起落架垂向变形为变量，基于虚功原理提出了系留载荷计算方法；金仲林[6]也利用遗传算法对甲板系留点进行了优化，而王丹[7]则采用ANSYS的优化功能对甲板系留点位置和系留索预紧力进行了优化。

系留索预紧力优化属于多变量连续空间优化问题，而基本蚁群算法优良高效的全局优化性能只能适用于离散的组合优化问题。最早使用蚁群算法对连续空间进行优化的是Bilchev和Parmee[8]采用遗传算法进行全局搜索，然后利用蚁群算法进行局部优化，但该算法在运行时会出现重复搜索同一区域的现象；Dreo等[9]提出了一种基于密集非递阶的连续交互式蚁群算法；段海滨等[10]提出了一种将连续空间离散化的改进蚁群算法；赵星乔[11]在连续域蚁群算法中加入自适应策略用以提高算法性能；高芳等[12]引入了进化算法中的变异操作，对寻优过程中每次迭代的最优解进行变异，增加了种群的多样性；黄敏等[13]针对各子区间内的总信息量及应有的蚁数的求解方式进行改进，引入一个随迭代次数增加而变化的函数，以提高改进后蚁群算法的收敛速度；刘文[14]通过对解空间定向式挖掘来实现全局快速搜索。本文采用文献[15]提出的嵌入确定性搜索的连续域蚁群算法对系留索预紧力进行优化，一方面为了提高搜索效率，加入了文献[11]提出的采用两只蚂蚁从两个极点同时搜索的策略，另一方面为防止算法过早陷入局部最优解，加入了文献[16]提出的MMAS策略。

1　直升机舰面系留载荷计算

1.1外力计算

舰船坐标系如图1所示，原点oS位于舰船摇摆中心，xS轴指向舰尾，yS轴指向右舷，zS轴垂直向上，惯性坐标系与静止时的舰船坐标系重合，但不随舰运动。

图1　舰船坐标系

机体坐标系如图2所示，原点oH位于机体纵剖面、舰面和机头垂直切面的交点，xH轴指向机尾，yH轴指向机体右侧，zH轴垂直向上。

图2　机体坐标系

重力在惯性坐标系下为G=[00-mg]，作用在机体重心。直升机所受风载Q=[QxQyQz]作用于形心，风载计算公式为：

(1)

式中，V为风速(相对舰船)，S为受风有效面积。

舰船的主要运动为横摇和纵摇，且在工程应用上一般看成是简谐运动，假设舰船横摇角为φ，纵摇角为ϑ。惯性坐标到舰船坐标变换矩阵为：

(2)

重力和风载在舰船坐标系下表示为：

(3)

直升机停机位的舰船坐标为(xSp,ySp,zSp)，惯性加速度在舰船坐标下表示为：

(4)

惯性力表示为IS=[-maSx-maSy-maSz]。机体xH轴与舰船xS轴夹角为α，舰船坐标到机体坐标变换矩阵为：

(5)

重力、风载和惯性力在机体坐标系下表示为：

(6)

1.2约束力计算

假设直升机在外载作用下相对于舰船的6个刚体位移为u、v、w、φ、θ、ψ。则机体任意点的位移可表示为：

(7)

式中，XH0为机体任意点在机体坐标中的初始值。

(8)

直升机在舰面系留受到的约束力由系留索和起落架提供，在机体坐标系下均可表示为：

fH=fH0+K等效s

(9)

式中，fH0为初始约束力，K等效为系留索或起落架的等效刚度。

根据达朗贝尔原理可列外力和约束力的平衡方程：

(10)

由上述方程可解出直升机的6个刚体位移u、v、w、φ、θ、ψ，从而可计算出系留索和起落架的载荷。

2　基于蚁群算法的系留索预紧力优化

设优化函数为minZ=f(X),在系留索预紧力优化问题中Z代表系留索最大张力Tmax，X代表预紧力T0。

系留索预紧力优化属于多变量连续空间优化问题。本文采用嵌入确定性搜索的连续域蚁群算法[15]，为避免算法过早陷入局部最优解，将各只蚂蚁所带信息素控制在[τmin,τmax]。具体思路如下：

(11)

(12)

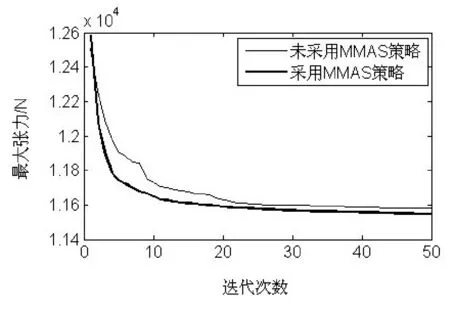
其中，a是随机数且0

(13)

其中，b是随机数且0

(14)

其中，dij=f(Xi)-f(Xj)，且第i只蚂蚁只能向其他目标函数更小的蚂蚁j进行移动，其中系数T决定概率函数的斜率，蚂蚁寻优转移如图3所示。

图3　蚂蚁寻优

蚂蚁向某个信息素更高的地方移动时，可能会在途中发现新的食物源，转移公式为：

(15)

其中，c、λ是随机数且0

(16)

其中，Δτ(i)=f(Xi)；0<β<1是残余因子。为防止算法陷入局部最优解，将每只蚂蚁所带信息素控制在一定范围：

(17)

3　实例仿真

3.1系留载荷计算方法验证

某研究所对某型直升机在某型舰船上系留做了试验，试验条件为：在机库内系留，机库内没有风力的影响；使用减摇鳍升摇，纵摇角度在0 度左右，横摇角度稳定在5 度左右，最大角度5.7 度；观测时间为180 秒，摇摆周期为12 秒左右；系留索预紧力在2000N左右[5]。直升机采用6条索具系留，具体布置如图5所示。

图4　系留索布置简图

对实验提供的各索具最大张力与本文计算值进行对比，结果如表1所示。

表1　结果对比

由表1可见，本文计算结果与试验结果基本吻合，6条索具平均相对误差仅为7.52 %。第1条索具误差较大主要是因为预紧力与实际施加预紧力不同，试验条件只给出各索具预紧力为2000N左右，而本文计算时6条索具均施加2000N预紧力。当各索具施加预紧力变为1000N时，索具1的最大张力由4820N降为3858N,说明预紧力对索具张力影响较大。

3.2优化实例

某型直升机采用16条索具进行系留，系留索布置如图5所示，主要计算参量如表2所示。

图5　系留索布置简图

参量数值重量/kg8840迎风风速/kn50侧风风速/kn35迎风面积/m210.9侧风面积/m242.5横摇幅值/(°)12.57纵摇幅值/(°)1.74横摇周期s10.5纵摇周期/s7横摇纵摇初始相位差/(°)0轮胎横向刚度/kN/m400轮胎纵向刚度/kN/m600轮胎垂向刚度/kN/m550系留索刚度/kN/m20000

为观察系留索张力完整的变化，取舰船一个运动周期对系留索张力进行计算，图6为系留索未施加预紧力时索具张力变化情况。

图6　无预紧力时的索具张力

由图6可见，系留索未施加预紧力时，索具6、8、15、16一直处于松弛状态，没有起到系留的作用，而索具13张力却达到17 978N，索具张力分布不均匀。

根据系留索布置对称的特点，索具1、2、3、4预紧力取值相同，索具5、6、7、8预紧力取值相同，索具9、10、11、12预紧力取值相同，索具13、14预紧力取值相同，索具15、16预紧力取值相同，预紧力均控制在[0N,10 000N]。采用嵌入确定性搜索的连续域蚁群算法，对系留索预紧力进行优化，图7为10次优化索具最大张力平均值随迭代次数变化曲线。

图7　10次优化最大张力的平均值

由图7可见，该蚁群算法在经过二十多步迭代后能够稳定地收敛下来，找到系留索最佳预紧力，且采用MMAS策略的结果优于未采用的结果。优化后，各索具预紧力取整后如表3所示。

表3　各索具预紧力

由表3可见，不同位置的系留索需施加的预紧力不同。无预紧力和预紧力优化后各索具最大张力对比如表4所示，预紧力优化后索具张力变化如图8所示。

表4　各索具最大张力对比

图8　预紧力优化后的索具张力

由图8可见，预紧力优化后，所有索具都没出现一直松弛的现象，且最大张力仅为11 682N,比未施加预紧力减少了35.02%，由表4可见预紧力优化后各索具张力比无预紧力时分布更均匀。

4　结　语

给出了直升机在舰面系留时的载荷计算方法，通过与试验结果对比验证了该算法的准确性。采用嵌入确定性搜索的连续域蚁群算法对系留索预紧力进行了优化，为了提高搜索效率，在

算法中采用两只蚂蚁从端点出发，另外为了防止算法过早陷入局部最优解，采用了MMAS策略。通过优化实例分析可知：(1) 运用该改进蚁群算法对直升机系留索预紧力进行优化，能快速地收敛到最优解，具有良好的收敛性和稳定性；(2)对系留索预紧力进行优化后，最大张力下降35.02%，且没有出现索具一直松弛的现象，优化效果明显。

[1] 孙淑苓,田石麟, 黄蓝.舰载直升机系留载荷及全机应力计算方法研究[J].航空学报, 1989,10(10):489-494.

[2] 李进军, 刘士光, 夏鸿飞.舰载直升机系留优化设计[J].华中理工大学学报,1996,24(8):94-96.

[3] 金海波, 戴元伦, 王云.考虑轮胎变形的系留计算模型研究[J]. 航空学报,2008,29(4):948-953.

[4] 李书, 何书恒, 徐丽娜. 舰载直升机系留座的布置优化[J]. 航空学报,2005,26(6):715-719.

[5] 吴靖, 胡国才. 基于弹性起落架的直升机系留载荷计算[J]. 海军航空工程学院学报, 2014,29(3):252-255.

[6] 金仲林. 舰载直升机系留座分布及系留载荷的仿真研究[D]. 南京: 南京航空航天大学, 2006.

[7] 王丹. 舰载直升机系留载荷分析及优化设计研究[D]. 哈尔滨: 哈尔滨工程大学, 2008.

[8]BilchevG,ParmeeIC.Theantcolonymetaphorforsearchingcontinuousdesignspaces[J].LectureNotesinComputerScience, 1995, 993:25-39.

[9]DreoJ,SiarryP.ContinuousInteractingAntcolonyalgorithmbasedondenseheterachy[J].FutureGenerationComputerSystems, 2004,20(5):841-856.

[10] 段海滨, 马冠军, 王道波,等. 一种求解连续空间优化问题的改进蚁群算法[J]. 系统仿真学报, 2007, 19(5):974-977.

[11] 赵星乔. 基于连续空间优化的蚁群算法[J]. 信息技术, 2011(4):47-52.

[12] 高芳, 韩璞, 翟永杰. 基于变异操作的蚁群算法用于连续函数优化[J]. 计算机工程与应用, 2011, 47(4):5-8.

[13] 黄敏, 靳婷, 钟声，等. 基于改进蚁群算法求解连续空间寻优问题[J]. 广西师范大学学报, 2013,31(2):34-38.

[14] 刘文.一种定向式挖掘的连续域蚁群算法[J].计算机科学,2013,40(12):292-294.

[15] 杨勇, 宋晓峰, 王建飞,等. 蚁群算法求解连续空间优化问题[J].控制与决策, 2003,18(5):573-576.

[16]StutzleT,HoosHH.MAX-MINantsystem[J].FutureGenerationComputerSystems,2000,16(9):889-914.

MOORINGCABLESPRELOADOPTIMISATIONFORSHIPBORNEHELICOPTERBASEDONANTCOLONYOPTIMISATION

WuJing1HuGuocai2

1(Graduate Students’ Brigade,Naval Aeronautical and Astronautical University, Yantai 264001,Shandong,China)2(Department of Airborne Vehicle Engineering,Naval Aeronautical and Astronautical University,Yantai 264001,Shandong,China)

Accordingtotheforceconditionofthehelicoptermooringontheship,weproposedacalculationmethodformooringloadwhichtakes6rigiddisplacementsofhelicopterasthevariants.Theoptimisationofmooringcablespreloadisaproblemofmultivariablecontinuousspaceoptimisation.Aimingatthischaracteristic,weusedtheACOalgorithmincontinuousdomainwiththedeterministicsearchembeddedtooptimisethemooringcablespreload,andaddedMMASstrategytothealgorithmtopreventitfallingintolocaloptimalsolutiontooearly.ResultsshowedthatthisACOalgorithmenabledtheobjectvaluestablyconvergingafteriteratingmorethan20steps,thuswellsolvestheproblemofthehelicoptermooringcablespreloadoptimisation.Finally,wemadethecomparativeanalysisonthemooringloadofacertaintypeofhelicopterwithoutthepreloadandwiththeoptimisedpreload.Whenwithoutthepreload,thecableswentonrelaxedandhavingnomooringrole,howeverthemaximumtensionofmooringcableshada35.02%decreaseafterthepreloadbeingoptimised,andthecablestensiondistributedmoreevenlyaswell.

HelicopterMooringPreloadAntcolonyoptimisation(ACO)Optimisation

2014-07-17。吴靖，硕士生，主研领域：飞行器动力学。胡国才，教授。

TP18

ADOI:10.3969/j.issn.1000-386x.2016.03.025