以数列为例谈“高观点”下的合理纠错

◇　河北　王习武

(作者单位：河北省滦平县第一中学)



以数列为例谈“高观点”下的合理纠错

◇河北王习武

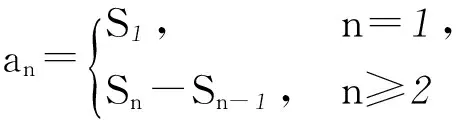
下面是一道典型的易错题:

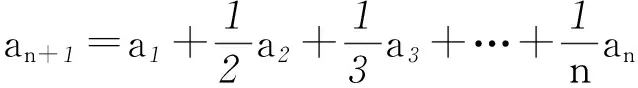
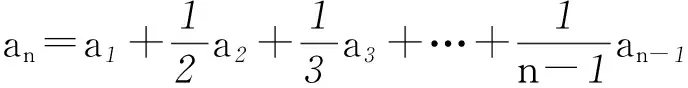
因为a1=1,an=2 004，所以an=n×1=2 004, 所以n=2 004.

上述答案是错的,正确答案是n=4 008.

错解分析为什么会错呢?是由于对n的取值范围理解不科学所致．因为有的同学仅仅认为只有在已知Sn求an时才讨论n=1．实际上,数列是函数思想的延伸,一个数列可以将an看成关于n的函数,因此数列的通项公式就如同函数的解析式,能够根据每个n的值,求出数列的每一项相对应的函数值，而n的取值范围就是数列的定义域．

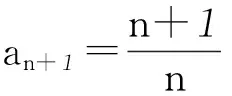
用这种观点,我们来进行下面的讨论.

1　什么时候需要“验证n=1”

2　什么时候不用“验证n=1”

我们再来看看下面的题目.

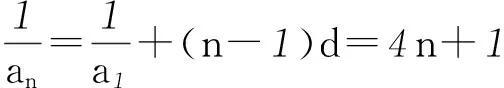
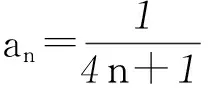
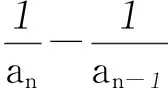
3　如何防止过度验证或者忽视验证

我们先来看下面的例题.

(n≥2),

an-1=a1+2a2+3a3+…+(n-2)an-2(n≥3).

所以an-an-1=(n-1)an-1,an=nan-1(n≥3),

又a1=1,a2=a1=1．所以正确答案是

上述过程中,大家会注意到在每次等式变形的后面,都添加上n的取值范围,就像函数的定义域一样,关注它的变化,不难判断最终需要“验证n=1”．

运用函数定义域的观点来认识“验证n=1”的现象,可以轻松应对所有的数列问题.这样一来我们不再是仅仅停留在“运用Sn求数列通项需要验证n=1”的狭隘认识上面了．其实,在处理其他很多问题时都需要“高观点”,这样同学们才能印象更深,理解更透彻．

再比如求解高次不等式时,常常需要按照“奇穿偶不穿”的原则画图求解.

首先要正确理解图形的实质,其次要透彻理解为什么“偶不穿”．前者学过导数就会明白图形的实质其实就是函数简图.后者,笔者认为不能说“偶不穿”,应该说“偶也穿”.因为偶重根穿过了之后,又回头了,最终效果看起来似乎是“没穿过”,这样理解也就没有所谓“奇穿偶不穿”,实际上是“见根就穿”．

(作者单位：河北省滦平县第一中学)