零航速减摇鳍升力特性数值研究

周　卫，张吉萍，许颂捷

（1.浙江海洋学院船舶与海洋工程学院，浙江舟山　316022；2.浙江省海洋渔业船舶交易服务中心，浙江杭州　310007；3.浙江省近海海洋工程技术重点实验室，浙江舟山　316022；4.上海羽翼船舶设备有限公司，上海　201600）

零航速减摇鳍升力特性数值研究

周卫1，2，张吉萍1，3，许颂捷4

（1.浙江海洋学院船舶与海洋工程学院，浙江舟山316022；2.浙江省海洋渔业船舶交易服务中心，浙江杭州310007；3.浙江省近海海洋工程技术重点实验室，浙江舟山316022；4.上海羽翼船舶设备有限公司，上海201600）

为了探究零航速减摇鳍周期摆动时产生的升力与转动频率、转角幅度、转轴位置以及来流速度几方面的关系，本文运用滑移网格技术对二维NACA0012翼型的周期摆动进行数值预报。研究表明：Transition SST湍流模型较其他常见湍流模型更适合分析大攻角周期摆动问题；对于转动方式满足余弦函数的减摇鳍，产生的升力随转角幅度、转动频率增加而增大，来流速度对升力的影响大于转轴位置。论文研究对零航速减摇鳍选型设计具有一定指导意义。

零航速；减摇鳍；升力特性；Transition SST；NACA0012

随着人们对低航速下的舒适性要求的提高，零航速减摇概念自提出便受到国内外机构及学者的关注，其工作原理是快速摆动鳍体，产生抵抗船舶横摇力矩，实现低航速或停泊状态的减摇。目前关于零航速减摇鳍的研究主要以试验研究为主，美国及荷兰相关机构在1998年开展了探索性试验研究［1-2］，昆腾公司利用试验方法开展全航速减摇鳍的初步设计［3］。在国内，金鸿章等［4］根据实验数据及势流理论构建零航速减摇鳍的力学模型，表明升力受旋转角速度、角加速度等因素的影响。

零航速减摇鳍的周期性摆动实际是以旋涡产生、耗散为主导的湍流运动，对于这种复杂的湍流运动，试验研究受试验器材和设备的限制，往往仅能提供有限的积分变量，而CFD数值方法能提供更完善的流场信息。同时伴随湍流模型的完善，及计算精度与稳定性的提高，运用数值方法进行零航速减摇鳍的研究具有较明显的优势。

本文以二维NACA0012翼型作为研究对象，运用Fluent软件自带的UDF函数编译各种运动方式，并结合滑移网格技术进行数值预报。针对试验工况，对各类湍流模型、网格大小等相关设置的影响进行分析，表明数值方法能较好的预报大攻角动态失速问题。其次针对减摇鳍运动特征，分析了转角幅度、转动周期、转轴位置、来流速度几方面对于升力的影响。

1　数值方法

1.1湍流模型

直接计算法和雷诺平均法（RANS）是进行数值分析的两种主要方法，RANS由于存在表示湍流脉动对平均流动影响的雷诺应力项τij，因此需要添加湍流模型进行封闭。常用的k-ω和k-ε湍流模型，由于存在较大耗散会制约旋涡的产生，无法准确的预报旋涡的产生的位置、旋涡扩散的过程［5］。因此，本文主要采用Transition SST模型进行分析减摇鳍的周期摆动问题。

Transition SST湍流模型是基于k-ω SST模型，同时考虑湍流转捩问题，因此运输方程还需构造关于动能厚度雷诺数Reθ和间歇因子γ的运输方程，并通过控制方程与SST k-ω模型结合起来。

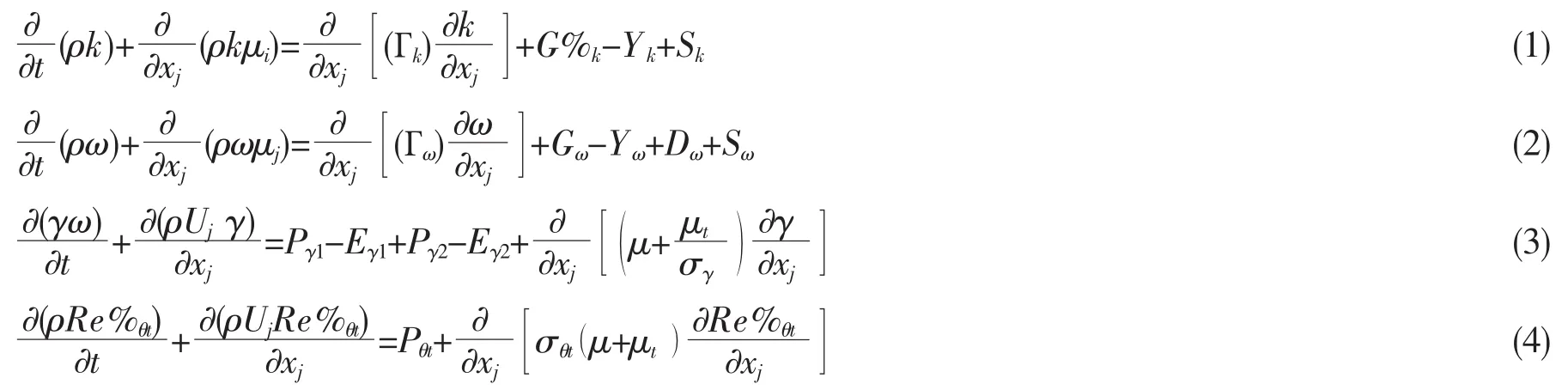
式（1）、（2）为SST k-ω湍流模型，式（3）、（4）为间歇因子γ及转捩雷诺数的运输方程；式（1）、（2）中：ρ为流体密度，μj对应速度矢量，xj对应位置矢量，Gk和Gω为关于k和ω的产生项，Гω、Гk为有效扩散项；Yω、Yk为各自的湍流耗散项，而Sω、Sk则表示为可自定义的源项。式（3）中Pγ1、Eγ1为过渡源项，Pγ2、Eγ2为破坏源项。

转捩模型与SST湍流模型结合的控制方程为：

G%k与Y*k为SST模型中的初始的生成项与耗散项。

1.2研究对象

目前，关于零航速减摇鳍的试验数据有限，因此文本选用LEE等［6］针对大攻角失速研究采用的NACA0012翼型作为研究对象。选用该试验数据进行验证分析主要有两方面原因：首先是该实验涉及大攻角翼型的雷诺数范围与减摇鳍摆动过程的雷诺数范围相近，同时空气与水的流动特性相近。其次，该试验得到的各项系数已剔除三维流动对是实验结果的影响，因此试验数据适用于二维的分析。NACA0012翼型的摆动原理具体设置可参见文献［6］。表1为数值计算涉及工况的主要参数。

表1　工况参数Tab.1　Parameters of Different Loadcases

1.3网格及计算设置

文中所计算的两种工况采用相同的网格进行计算，网格利用ICEM软件的O型网格形式进行划分，翼型表面初始网格高度为0.02mm，满足y+值小于1要求，网格沿法线方向的高度以1.2比率增长，确保能捕获近壁面附近的小尺度脉动同时降低网格数量，最终确定的初始网格数量为12万。在此基础上，弦长方向上的网格加密1.5倍，分别生成18万和27万网格。

图1　NACA翼型表面网格Fig.1　Surface Mesh of NACA Airfoils

图2　计算域及边界条件Fig.2　Calculation Domain and boundary conditions

数值计算采用的边界条件与试验条件相同，具体设置如下：入口位置：翼前18倍弦长，设置为速度入口；远场条件：距翼型18倍弦长，设置为速度入口；出口位置：翼后24倍弦长位置，设置为压力出口；Interface边界：距翼型10倍弦长。

本文涉及的计算均采用双精度基于压力法求解器进行求解，对流项采用二阶迎风差分格式，压力速度差分方程组的偶合求解采用SIMPLE格式，采用中心差分格式进行离散。对于DDES湍流模型，采用有界中心差分格式。运用滑移网格技术以及UDF函数实现不同运动方式的控制。

2　计算结果与分析

2.1验证工况分析

图3为时间步长是0.000 2 s下，不同湍流模型计算得到升力系数。对于所有湍流模型对于从-5°到25°的上扬阶段准确性均优于25°到-5°的下摆阶段，无论是升力变化趋势还是与试验结果的差值。

上摆阶段：角度满足-5°≤α≤25°范围时：RNG k-ε、DDES、Transition SST三种湍流模型均做出较好的预报，在20°≤α≤25°范围，三种湍流模型表现较大差异，DDES模型预报的失速角度为21°，且升力系数峰值较实验值偏小15.6%；RNG k-ε模型则升力系数随转角增大而保持震荡增加，并未出现明显的失速现象，这是由于RNG k-ε模型无法模拟前缘涡分离现象。Transition SST模型预测的失速角度为24.5°，25°时的升力系数下降约0.9，表明Transition SST模型过度预报分离现象，将直接影响下摆过程的准确性。

下摆阶段：采用加强避免函数处理的RNG k-ε得到的升力系数变化较为平稳，与试验结果吻合较好；Transition SST模型和DDES模型在15°≤α≤25°范围，升力系数波荡较大，这是由于过度预报分离现象，造成的二次分离预报不准确。在15°≤α≤25°，Transition SST模型预报的升力系数的震荡现象减小明显，趋势与实验结果吻合。

图4为12万、18万、27万网格采用Transition SST模型、时间步长采用0.0002 s时计算得到的升力系数。上扬阶段：三种网格得到的升力系数几乎贴合，在20°至25°过程，12万网格与其他网格得到升力系数数值差异较大；下摆阶段：三种网格得到升力系数变化趋势整体保持一致，27万网格与试验结果的数值差异最小。整体而言，18万网格策略为较优的网格策略，在后续的计算分析中采用18万网格进行研究分析。

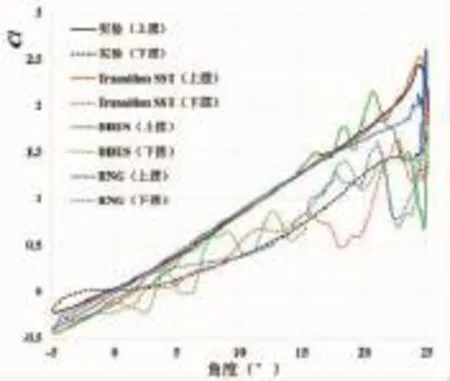
图3　不同湍流模型的升力系数Fig.3　Lift Parameters of Different Turbulence Models

图4　不同网格划分的升力系数Fig.4　Lift Parameters of Different Mesh

2.2零航速数值分析

零航速减摇鳍的运动方式主要有两种，一是采用加速-匀速-减速的运动方式［7］，二是满足余弦运动规律，文中采用第二种运动方式进行分析，并对转角幅度、转动周期对升力影响进行分析。

图5　不同转角幅度的升力变化曲线Fig.5　Lift Curve of different Angle Ranges

图6　不同转角周期的升力变化曲线Fig.6　Lift Curve of different Angle Periods

图5为零航速减摇鳍的转动周期为1 s，转角幅度分别为35°、40°、45°、50°时的升力变化曲线，由图5可以看到，四种转角幅度的升力曲线在上扬或下摆阶段升力峰值均经历先增大后减小的过程。下摆阶段除转角幅度为50°时升力峰值位于11°附近，其他转角幅度的升力峰值出现在0°（最大角速度位置）附近；上扬阶段所有转角幅度的升力峰值均出现在12°附近，即超前于最大角速度所在位置，这是由于附连水质量力的影响。此外，转角幅度增加5°，下摆阶段升力峰值平均增幅约35%，上扬阶段升力峰值平均增幅约22%。

图6对应的是转角幅度为40°，转动周期分别为0.5 s、1 s、2 s时的升力变化曲线。通过比较可以发现，三种周期下的升力峰值出现的位置基本一致，升力峰值与转动周期的平方成反比，即升力峰值与转动角速度平方成正比。

图7　不同转轴位置的升力变化曲线Fig.7　Lift Curve of different Rotor Positions

图8　不同流速下的升力变化曲线Fig.8　Lift Curve of different Velocitys

图7为四种转轴位置的升力变化曲线，鳍轴位置向前移动，升力变化趋势基本保持不变，上摆过程的升力峰值增大，下摆过程的升力峰值减小。由图8可以看到，流速达到0.2m/s时的升力变化趋势和升力峰值均与航速低于0.1m/s时发生明显变化，上摆和下摆过程升力变化趋势相似、升力峰值相近，表明零、低航速时减摇鳍的升力变化受航速影响较大。

3　结论

本文利用数值方法对零航速减摇鳍上下摆动过程中涉及的大攻角动态失速问题进行研究，通过上述的分析可以得到以下结论：

（1）对于大攻角动态失速问题，Transition SST湍流模型的预报结果优于常用的RNG k-ε湍流模型，DDES湍流模型存在过度预报旋涡分离现象。

（2）运动规律满足α=α1cos（2πf·t）的零航速减摇鳍，在转动过程中减摇鳍产生的升力与转角幅度成正比、同时与转动周期的平方成反比。改变鳍轴位置对于升力的变化影响不大，来流速度对于减摇鳍的性能影响明显。

（3）对于零航速减摇鳍设计初期，可利用数值方法辅助开展翼型评估、转轴位置分析、转动形式优化等方面工作。

［1］DALLINGA R P.Roll stabilization of motor yacht：Use of fin stabilizers in anchored conditions［Z］.Project 99，Amsterdam，1999.

［2］DALLINGA R P.Roll stabilization of motor yacht：Hydrodynamic aspects of the comparison of anti-roll tanks and fins［Z］. Project 2002，Amsterdam，2002.

［3］OOMS J.The use of roll stabilizer fins at zero speed［Z］.Project 2002，Amsterdam，2002.

［4］金鸿章，张晓飞.零航速减摇鳍升力模型研究［J］.海洋工程，2007，25（3）：83-87.

［5］ANSYS.ANSYS FLUENT 12.0 Theory Guide［Z］.Ansys Inc，USA，2009.

［6］LEE T，GERONTAKOS P.Investigation of flow over an oscillating airfoil［J］.Journal of Fluid Mechanics，2004，512：313-341.

［7］宋吉广.基于升力反馈的全航速减摇鳍研究［D］.哈尔滨：哈尔滨工程大学，2010.

Research on Lift Characteristics of Zero-speed Fin Stabilizer

ZHOU Wei1，2，ZHANG Ji-ping1，3，XU Song-jie4
（1.School of Naval Architecture and Ocean Engineering，Zhejiang Ocean University，Zhoushan316022；2.Zhejiang Province Marine Fishing Vessel Trading Service Center，Hangzhou310007；3.Key Laboratory of Offshore Engineering Technology of Zhejiang Provine，Zhoushan316022；4.Yoyeah Marine，Shanghai201600，China）

To explore the influence from rotational frequency，angle range，rotor position and flow velocity to the cyclic swing lift of Zero-speed Fin Stabilizer，the numerical forecast to the cyclic swing of two-dimensional NACA0012 airfoils is carried out with the sliding mesh technique.The following conclusions can be obtained：Transition SST turbulence model is more appropriate to analysis the cyclic swing at high angles of attack that other turbulence models；to the fin stabilzer with the rotating mode meeting the cosine function，the lift increased with the increasing of angle range and rotational frequency，and the influence from the flow velocity to the lift is more than the influence from the rotor position.The research is of guiding significance to the type selection and design of zero-speed fin stabilizer.

zero-speed；fin Stabilizer；lift characteristics；Transition SST；NACA0012

U664.72

A

1008-830X（2016）02-0150-05

2015-11-23

浙江省自然科学基金（LY14E090002）；国家自然科学基金（51409232）

周卫（1987-），男，硕士研究生，研究方向：农业机械化.