具有变号位势和非线性项的薛定谔方程的无穷多解

吕定洋

（湖南第一师范学院 数学与计算科学学院，湖南 长沙 410205）

具有变号位势和非线性项的薛定谔方程的无穷多解

吕定洋

（湖南第一师范学院 数学与计算科学学院，湖南 长沙 410205）

本文用不同于已有文献的方法研究了一类薛定谔方程的无穷多高能解的存在性，其中位势V（x）允许变号，的原函数所满足的超二次条件与（AR）型条件互为补充。

薛定谔方程；超二次条件；变号位势；高能解

引言

本文考虑如下的半线性薛定谔方程：

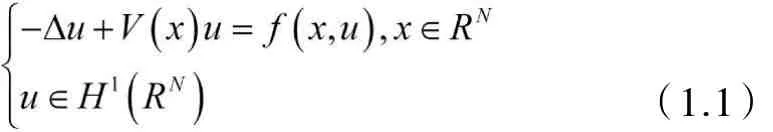
该方程不但在物理应用方面有重要的作用，也为数学方法的发展提供了一个很好的模型.利用变分法，方程（1.1）的非平凡解的存在性和多重性得到了广泛研究，参见文献［1-4］，在大多数参考文献中，以下的（AR）条件被经常使用：（AR）存在μ＞2，使得其中F（x，u）=（.AR）条件的作用是用来证明（PS）序列的有界性，这对临界点理论的应用是非常重要的.但有许多函数并不满足（AR）条件，如在文献［5，6］中，作者建立了一些新的超二次条件来代替（AR）条件，其中有些比（AR）条件弱，有些与它互为补充.在最近的文献［7］中，Qingye Zhang等在对V和f做出一些新的假设的情况下，得到了方程（1.1）无穷多非平凡解的存在性结论.在本文中，我们对V和f做如下假设：，且；（）存在一个常数d0，使得

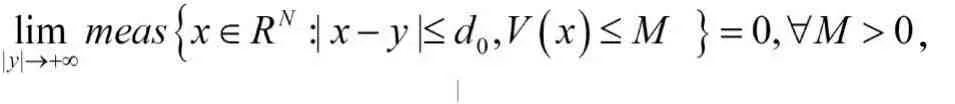
其中meas（.）定义为RN中的勒贝斯格测度.，且存在常数，使得

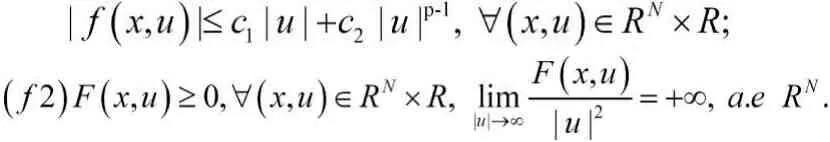
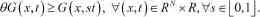
其中

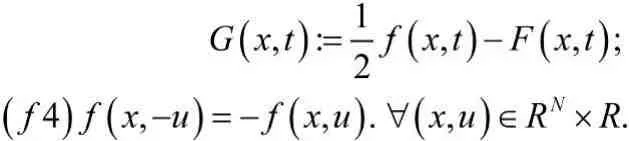
定理1.1假设（V1），（V2），（f1）-（f4）成立，则问题（1.1）有无穷多解｛uk｝，其对应能量值趋于无穷大.注：1：在我们的假设中V（x）是允许变号的.

2：条件（f3）是由Jeanjean在文［6］中提出的，它比常见的单调性假设弱.有很多函数如前面提到的.满足 f（3）但不满足（AR）条件，条件f（2），f（3）与（AR）条件互为补充.

3：我们的定理的证明方法完全不同于文［7］的证法.

1.变分框架

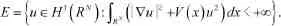
进一步，我们有：

现在，我们在E中定义一个泛函：

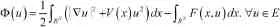
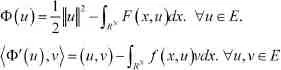
定义2.2称泛函I满足（C）C条件是指，对任意一列，若满足和则｛un｝必有收敛子列，其收敛极限是泛函I的临界点.引理2.3（对称山路定理 ［2，9］）设X是有限维Banach空间，其中Y是有限维的.如果满足（C）C条件（c＞0），且

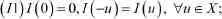
那么I存在无界临界值序列.

2.定理证明

（1）证明Φ满足（C）C条件。

那么wn在E中弱收敛于w.

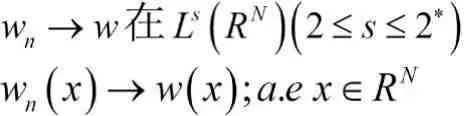
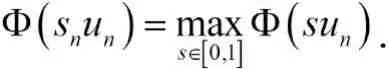
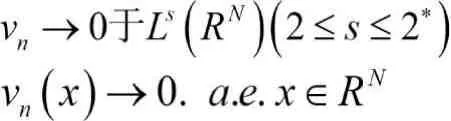
因此，利用Lebesgue控制收敛定理和（2.1）有：

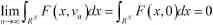
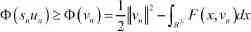
（因为m的任意性）.

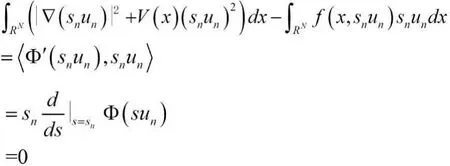
因此，利用f（3），

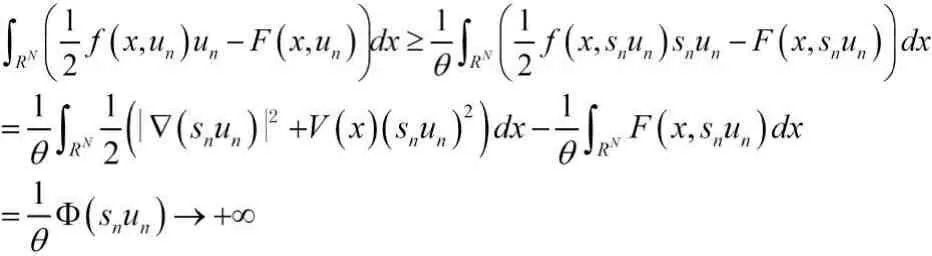
矛盾.所以｛un｝在E中有界.

（2）证明｛un｝有收敛子列.

不妨假设在E中un弱收敛于u，据引理2.1知，在空间.中，un→u.

由un弱收敛于u知，.根据假设（f1），.

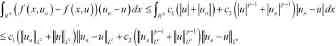
（3）验证泛函Φ满足引理2.3中的其他剩余条件.

（I1）显然Φ（0）=0.由（f4）知Φ（-u）=Φ（u）.

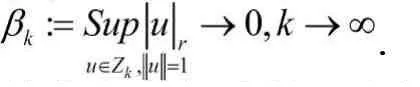
故我们可以选择一个整数m≥1，使得

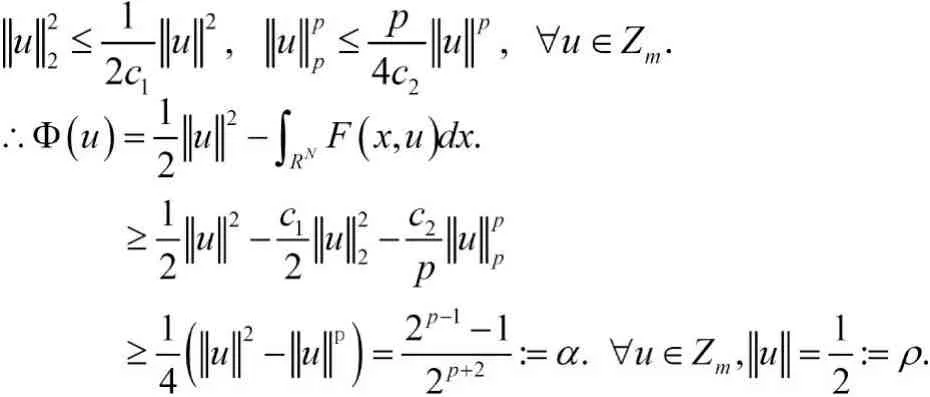
根据（V1）知，存在一个常数V0＞0，使得

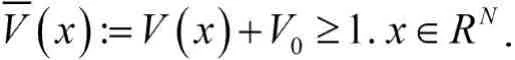
引理2.4问题（1.1）与下列问题是等价的.

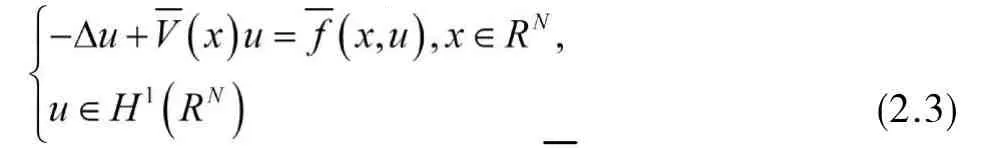
让X=E，Y=Ym，Z=Zm.显然，满足 （f1），（f2），（f3），（f4），从而由上面的证明知系统（2.3）具有无穷多高能解.再由引理2.4知，问题（1.1）也具有无穷多高能解.定理证毕。

［1］A.Ambrosetti,P.H.Rabinowitz.Dual Variational methods in Critical point theory and applications,［J］.1973,14（4）：349-381.

［2］T.Bartsch,Z.Q.Wang.Existence and multiplicity results for some suplinear elliptic problems［J］.1995,（20）：1725-1741.

［3］T.Bartsch,M.willem,Infinitely many nonradial solutions of a Euclidean Scalar field equation［J1993,（117）：447-460.

［4］Y.H.Ding,Infinitely many entire solutions of an elliptic system with Symmetry［J］.1997,（9）：313-323.

［5］Y.Ding,A.Szulkin,Bound states for semilinear equations with sign-changing potential［J］.,2007,29（3）：397-419.

［6］L.Jeanjean,On the existence of bounded palais-smale sequences and Application to a Landesman-Lazer type problem set on［J］.1999,（129）：787-809.

［7］Q.Zhang,B.Xu,Multiplicity of solutions for a class of semilinear schrodinger equations with sign-changing potential［J2011,（377）：834-840.

［8］T.Bartsch,Z.-Q.Wang,M.Willem,The Dirichlet problem for superlinear Elliptic equations［A］.M.Chipot,P.Quittner（Eds.Elsevier,2005.

［9］P.H.Rabinowitz,Minimax methods in critical point theory with appiications to differential equations［Z］.in：CBMS Reg.Conf.in Math.,Vol.65.Amer.Math.Soc., Providence,RI,1986.

［责任编辑：胡伟］

Infinitely Many Solutions for a Class of Schrodinger Equations with Sign-changing Potential and Nonlinearity

LV Ding-yang

（Department of Mathematics,Hunan First Normal University,Changsha,Hunan 410205）

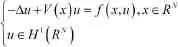
Schrodinger equations；super-quadratic；sign-changing potential；high energy solutions

O175

A

1674-831X（2016）02-0097-03

2015-05-12

湖南省自然科学基金项目（14JJ7083）；湖南省教育厅科学研究项目（14C0253）

吕定洋（1968-），男，湖南邵阳人，湖南第一师范学院数学与计算科学学院副教授，主要从事偏微分方程临界点理论。