漂移—扩散模型的蒙特卡洛随机仿真

王玉辉

（湖南第一师范学院 信息科学与工程学院，湖南 长沙 410205）

漂移—扩散模型的蒙特卡洛随机仿真

王玉辉

（湖南第一师范学院 信息科学与工程学院，湖南 长沙 410205）

为比较直接蒙特卡洛仿真与基于随机游走的蒙特卡洛仿真的精度，使用数值仿真对粒子漂移和扩散过程中的一阶、二阶和二阶中心矩的相对误差进行了测试。实验结果表明，两种方法的精度和性能大致相当。因此，在漂移—扩散模型的蒙特卡洛随机仿真中，固定或变化的时间步长可以根据需要和连续空间或离散网格灵活组合使用，并不会严重影响仿真的精度。

蒙特卡洛随机仿真；漂移—扩散；随机游走；仿真精度

漂移—扩散是各种物理、化学、生物系统中一种常见的现象。对于这类漂移—扩散或更复杂的反应—漂移—扩散模型，当问题的解析解难以求得或明确需要采用单个粒子追踪等方法模拟粒子的微观、随机运动过程时，蒙特卡洛随机仿真就成了求解这类模型的一种重要方法［1］。

相对而言，直接蒙特卡洛仿真和基于随机游走的蒙特卡洛仿真是两种较为常见和经典的随机仿真方法。前者根据漂移-扩散模型在自然边界条件下解的形式，使用随机的、服从正态分布的跳跃步长和固定或变化的时间步长，在连续空间中模拟粒子的运动。后者则使用固定网格步长以及固定或服从一定概率分布的随机时间步长，根据一定的停留概率和到邻近网格的转移概率，在离散网格格点上模拟粒子运动［2］。

一般而言，蒙特卡洛随机仿真的精度主要取决于算法自身带来的误差和伪随机数产生器等因素。但是，目前有关蒙特卡洛随机仿真的算法精度的研究相对比较少，更难以从理论上进行分析。对于基于随机游走的蒙特卡洛仿真，若网格步长足够精细，其精度原则上可以无限逼近连续系统模型对应的解析解［3］。为了定量分析和比较以上两种蒙特卡洛仿真的精度，为具体应用实践中的算法选择和时间步长、网格步长等仿真参数选择提供参考，可以使用粒子漂移-扩散过程中的一阶、二阶和二阶中心矩的相对误差度量和评估仿真精度，通过数值仿真方法进行实验测试和验证。

1蒙特卡洛随机仿真算法

不失一般性，考虑一维空间具有恒定扩散系数D、漂移速度q的漂移-扩散模型［4］：

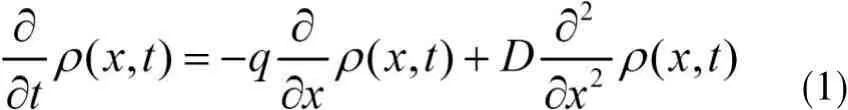
在自然边界和初始条件下，其解析解为：

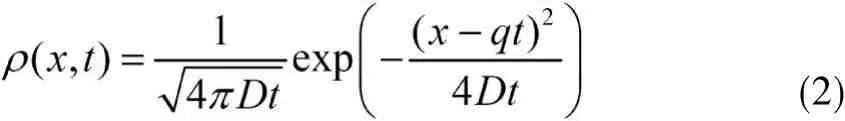
任意时刻，相应的均值和方差为：

原则上，蒙特卡洛随机仿真的目标是精确模拟和复现上述公式（3）和（2）描述的粒子宏观运动特征和微观分布状态。

2.1直接蒙特卡洛仿真算法

直接蒙特卡洛仿真的思想比较简单：根据公式（2）描述的粒子概率密度分布函数及给定的时间步长，可推断下一时刻粒子的位置分布服从正态分布。因此，可以直接使用正态分布进行随机采样，得到一个随机的跳跃步长，再使用该步长更新粒子的位置。对所有粒子重复上述过程，直至仿真结束，即可实现蒙特卡洛随机仿真。

显然，上述随机跳跃步长采样将导致粒子在连续空间的位置更新。若设定一个网格尺寸，可以将粒子在连续空间的位置映射到网格格点中，但同时仍需保留在连续空间中的位置状态变量。否则，可能影响和降低仿真的精度。

原则上，直接蒙特卡洛仿真可以使用固定或者变化的时间步长。步长的大小只影响仿真的时间分辨率，而不会对仿真的精度产生太大的影响。因而，该方法具有简单、直观、灵活的优点。

2.2基于随机游走的网格蒙特卡洛仿真算法

采用网格蒙特卡洛仿真算法对漂移-扩散模型进行求解首先需要将问题物理空间划分为网格（通常为均匀网格）。然后，计算网格中的粒子在离散的时间步长上在当前网格格点中的停留概率及向邻近网格格点的转移概率，同时按照一定概率分布对时间步长进行采样，由此追踪粒子在不同网格格点间的漂移-扩散过程。显然，以上转移概率、停留概率和时间步长均与网格步长有关。

对于公式（1）中的漂移—扩散模型，假设网格步长为λ，则一个连续时间随机游走粒子的首次跳出当前网格的时间概率密度分布可以用以下解析形式给出：

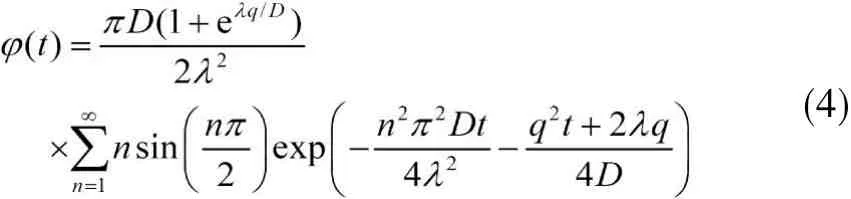
向左右两侧转移的时间积分概率为：

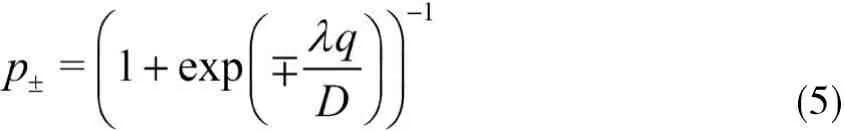
原则上，根据公式（4）和（5）即可设计出一个基于连续时间随机游走的蒙特卡洛仿真算法［5］：首先根据公式（4）进行采样，得到一个随机的时间步长，再随机产生一个在［0，1］区间均匀分布的随机数，根据公式（5）计算和确定该粒子跳跃和转移到的网格格点。事实上，由于公式（4）涉及无穷项级数的求和运算，而很多数值计算应用需要固定时间步长算法，因而需要对上述算法进行改进。其主要思路是通过一个等价的离散时间随机游走模型代替连续时间随机游走模型，同时保证正确地复现粒子分布的均值和均方位移等特性［2］。

为方便比较分析，公式（4）的Laplace变换为：

使用Taylor展开公式，可以得到首次跳出时间的一阶和二阶矩：

假设使用一个固定时间步长随机游走模型，其首次跳出时间的概率分布密度函数为：

其中，τ为时间步长，p0为停留概率，δ为Dirac函数。易知，公式（10）对应的Laplace变换为：

同样使用公式Taylor展开，可得：

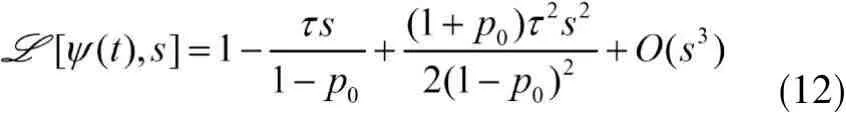
比较公式（12）和公式（7）中的系数，可得以下关系：

根据公式（13）和（14）即可构造固定步长的网格蒙特卡洛仿真算法：首先根据给定的网格步长λ、飘移速度q和扩散系数D，计算停留概率p0和时间步长τ，在每个时间步长上，对每个粒子随机产生一个在［0，1］区间均匀分布的随机数，根据公式（13）计算和确定该粒子是否跳跃；若是，再产生一个在［0，1］区间均匀分布的随机数，根据公式（5）计算和确定转移到的网格格点。重复上述过程，直至仿真结束。

实际上，为了提高效率，可以将公式（13）和公式（5）结合，每次只采样产生一个随机数，即可确定其下一时刻的位置。

对于固定步长的网格蒙特卡洛仿真算法，当网格步长和飘移—扩散参数给定时，即可唯一地确定时间步长、停留概率和转移概率。使用其他时间步长或者变化时间步长都将损害仿真的精度，甚至导致不正确的结果。

2.数值结果

为了分析比较以上两种仿真算法的精度，根据公式（3）给出的理论值，可以使用粒子在漂移-扩散过程中的一阶、二阶和二阶中心矩的相对误差对仿真精度进行度量和评估：

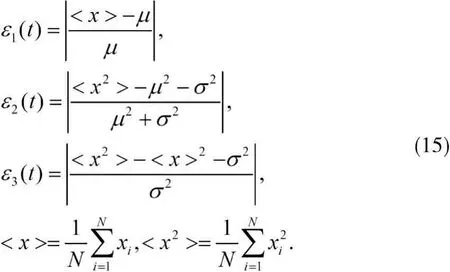
根据第2节中的蒙特卡洛仿真算法，使用标准C++语言编程，利用boost软件库提供的随机数生成器，不难实现上述的直接蒙特卡洛仿真算法和固定时间步长的网格蒙特卡洛仿真算法。

为了进行数值仿真和便于比较分析，实验中选择使用一个固定的扩散系数和相对变化的其他参数，具体参数设置如表1中所示。

表1　飘移—扩散模型仿真参数设置

，其取值在0.025到10之间，从而使仿真实验具有较好的代表性。数值仿真使用Windows8 64位操作系统，直接蒙特卡洛仿真算法采用和网格蒙特卡洛仿真算法相同的固定时间步长。服从均匀分布和正态分布的随机数生成均使用Mersenne Twister算法，以尽可能降低伪随机数产生器带来的误差。仿真过程中，在每个时间步长上，计算粒子漂移-扩散的一阶、二阶和二阶中心矩的相对误差，取平均记录分析。其中，直接蒙特卡洛仿真算法得到的粒子位置需要将其映射到网格格点上之后，再计算相对误差。

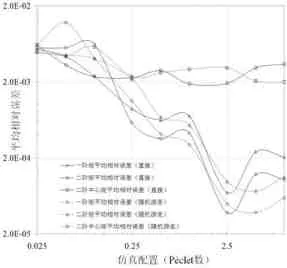
图1　平均相对误差（粒子数目N=104）

对于不同的仿真配置和Péclet数，得到的一阶、二阶和二阶中心矩的平均相对误差分别在图1（粒子数目N=104）和图2（粒子数目N=105）中绘出。其中，实线代表直接蒙特卡洛仿真结果，虚线代表基于随机游走的固定步长网格蒙特卡洛仿真结果。为了清楚显示，图中的坐标轴采用双对数刻度方式。注意图1和图2中纵坐标刻度的不同。

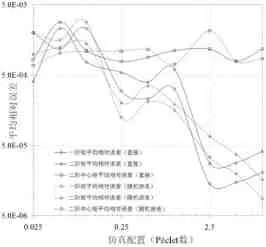
图2　平均相对误差（粒子数目N=10^5）

根据以上结果，易见：（1）不管粒子数目的多少，就一阶、二阶和二阶中心矩的平均相对误差而言，两种仿真方法的数值精度基本相当；（2）对于不同配置参数和Péclet数，相对于一阶和二阶矩而言，二阶中心矩的平均相对误差的变化较小；（3）增加粒子数目或仿真次数，可以显著降低两种仿真方法的平均误差，仿真精度提高的程度符合蒙特卡洛仿真的规律；（4）对于相同的漂移—扩散模型参数，网格步长的大小对仿真精度的影响相对较小，这表明两种算法均比较稳定；（5）一般而言，漂移速度越大，平均相对误差越小，这可能与一阶、二阶矩的绝对取值有关，而二阶中心矩的理论取值仅与扩散系数有关，因而其平均相对误差变化较小。

为了进一步得到两种仿真方法的直观结果，图3中给出了在一种典型配置条件（扩散系数、漂移速度、网格步长均为1，粒子数目为10^5，仿真次数为10）和不同时刻的粒子分布的概率密度曲线。其中，实线和虚线代表通过公式（2）计算的不同时刻的理论值，实心和空心的圆圈或方块分别代表直接蒙特卡洛仿真和基于随机游走的固定时间步长网格蒙特卡洛仿真结果。

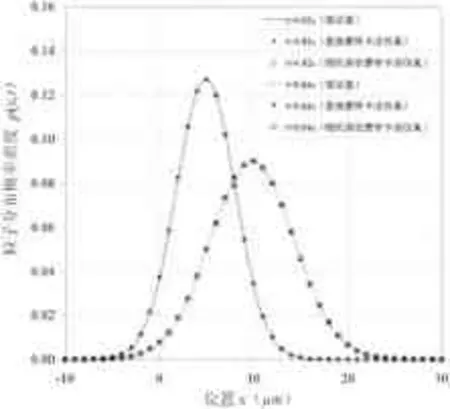
图3　不同时刻的粒子分布概率密度

由图3可以看出，两种不同仿真方法得到的不同时刻粒子分布概率密度与理论值的误差都很小，仿真精度也基本相当。

就仿真算法的时间性能而言，两者也相差无几。其原因是，除了随机数采样使用不同的分布函数之外，两种仿真方法使用基本相同的算法流程。而两种仿真方法均使用相同的Mersenne Twister核心算法，经变换后得到服从正态或均匀分布的随机数，因而，所需的计算时间也相差不大。因此，两者的运行时间性能基本相当，这与实际测试得到的结果完全一致，因此不再给出具体数值结果。

值得注意的是，对于蒙特卡洛仿真的精度评估还有其他度量指标和方法。但是对于分析比较两种蒙特卡洛仿真的精度而言，上述基于一阶、二阶和二阶中心矩的平均相对误差以及不同时刻的粒子分布概率密度的仿真结果已经能够基本上证明两者具有大致相当的精度。

此外，在仿真实验中测试得到的误差不仅包含算法自身带来的误差，还包括伪随机数产生器的误差。进一步的研究还应考虑不同的伪随机数产生器对仿真结果和精度的影响，从而更准确地评估不同仿真算法的真实性能。

结论

蒙特卡洛随机仿真是求解漂移—扩散模型的一类重要方法，其精度主要取决于算法自身带来的误差和伪随机数产生器等因素，而算法的精度直接决定着仿真结果的可信度。

针对用于漂移—扩散模型的直接蒙特卡洛仿真方法和基于随机游走的蒙特卡洛仿真方法，使用数值仿真对粒子漂移和扩散过程中的一阶、二阶和二阶中心矩的平均相对误差进行了测试，分析和比较了两种不同方法的精度。实验结果证实两种方法具有大致相当的仿真精度和时间性能。因此，在漂移-扩散模型的蒙特卡洛随机仿真中，固定或变化的时间步长可以根据实际需要和连续空间或离散网格灵活组合使用，而不会严重影响仿真的精度。

进一步的研究应充分考虑伪随机数产生器在蒙特卡洛仿真中带来的误差以及影响，因为一旦正确设计和实现了蒙特卡洛仿真算法，其精度将主要取决于伪随机数产生器的好坏。而在蒙特卡洛仿真中，通过严格随机性指标测试的伪随机数产生器并不一定意味着带来较高的仿真精度。除了采用粒子漂移和扩散过程中的一阶、二阶和二阶中心矩的平均相对误差进行仿真精度分析评估外，还可以考虑其他可能的度量指标和评估方法，对两种不同的仿真算法精度进行更全面评估。此外，将上述蒙特卡洛仿真算法扩展到多维、非均匀的漂移-扩散模型或更复杂的反应-漂移-扩散模型及利用并行仿真方法［9］和计算设备如图形处理单元以提高仿真的性能，都是值得深入研究的方向。

［1］M.E.J.纽曼,G.T.巴克马.统计物理学中的蒙特卡罗方法（第1版）［M］.北京：世界图书出版公司,2013.

［2］M.G.Gauthier,G.W.Slater.Building reliable lattice Monte Carlo models for real drift and diffusion problems ［J］.Physical Review E,2004,70（015763）.

［3］M.V.Chubynsky,G.W.Slater.Optimizing the accuracy of lattice Monte Carlo algorithms for simulating diffusion［J］.Physical Review E,2012,85（016709）.

［4］谢定裕.流体力学［M］.天津：南开大学出版社,1987.

［5］E.W.Montroll,H.Scher.Random walks on lattices：IV. Continuous-time walks and influence of absorbing boundaries［J］.Journal of Statistical Physics,1973,9（2）, 101-135.

［6］花嵘,傅游,康继昌.直接蒙特卡洛问题的并行化方法［J］.计算机工程,2004,30（5）,40-42.

［责任编辑：胡伟］

Monte Carlo Stochastic Simulation of Drift-Diffusion Models

WANG Yu-hui

（Department of Information Science and Engineering,Hunan First Normal University,Changsha,Hunan 410205）

To investigate the accuracy of Direct Monte Carlo simulation and Random-Walk-based Monte Carlo simulation,numerical simulations are carried out to measure the relative errors introduced in the first two moments and the second central moment of the displacement of particles during the drift-diffusion process.It turns out that both the accuracy and the performance of the two approaches are almost identical.Therefore,it is concluded that for such Monte Carlo stochastic simulation of drift-diffusion models,fixed or variable time steps can be used in a flexible manner with either discrete lattice or continuous space without significant degrade of accuracy.

Monte Carlo stochastic simulation；drift-diffusion；random walk；simulation accuracy

TP391.9

A

1674-831X（2016）02-0105-04

2014-11-12

王玉辉（1979-），女，湖南长沙人，硕士，湖南第一师范学校信息科学与工程学院讲师，主要从事计算机仿真研究。