基于变基床系数下双参数模型的管棚力学机理研究
卢新建
(福建省建筑科学研究院 福建福州 350000)
基于变基床系数下双参数模型的管棚力学机理研究
卢新建
(福建省建筑科学研究院福建福州350000)
针对常基床系数下管棚弹性地基梁模型的缺陷,分析了掌子面前方岩土体基床系数分布规律,基于 Pasternak 弹性地基梁理论,建立了变基床系数下管棚的力学模型,推导了管棚的挠度方程和内力计算公式,并提出求解方法。结果表明:考虑掌子面水平位移影响能较好地反映管棚在隧道开挖过程中的力学行为,更符合实际情况。
隧道;管棚超前预支护;变基床系数;Pasternak模型;力学机理
0 引言
近年来,国内外学者对管棚预加固机制进行了大量的研究,主要包括现场试验研究、解析分析、数值模拟分析与离心模型试验研究等。但由于地下工程的影响因素复杂多变,管棚预支护体系的许多基础理论问题仍缺乏系统的定量研究,管棚预支护的设计方法仍然是依赖于工程经验的工程类比。因此,进一步研究管棚预支护体系的力学机理,有利于更好地指导复杂地质条件下地下工程的施工,具有重要的现实意义。
本文针对常基床系数下管棚地基梁模型不考虑掌子面水平变形的缺陷,分析掌子面前方土体基床系数的分布规律,建立可考虑掌子面水平位移影响的基于变基床系数下双参数模型的管棚力学模型,推导了管棚的挠度方程和内力计算公式,并提出求解方法,对管棚的受力和变形进行了深入探讨。
1 土的理想化模型
1.1土的理想化模型选取
本文采用Pasternak模型来模拟隧道开挖过程中管棚与围岩之间的相互作用。Pasternak模型为模拟土体之间的连续性,假设在各独立的Winkler弹簧单元与一层只能剪切变形而不可压缩的薄层相连,如图1(a)所示。其外荷载作用下引起的变形如图1(b)所示。外荷载与位移之间的关系为:
(1)
式中:k和G为土体参数。
1.2Pasternak模型参数确定
(1)Pasternak模型参数确定
对于Pasternak模型参数确定,文献[1]采用变分法推导有限深弹性地基双参数模型,并按照土中应力分布规律给出了矩形均布荷载作用下模型参数的计算方法:
(2)
(3)
式中:E——土体弹性模量,MPa;
H——土体深度;
μ——土体泊松比;
A、B——矩形荷载长短边;
γ——反应A/B影响的无量纲参数,其取值见表1。

表1 γ的取值
对于管棚荷载,A≫B,此时γ可取1.00。H较大时,k0=G0=1,此时k、G的计算式可简化为:
(4)
(5)
由式(2)~(5)可见,荷载的形状和尺寸对模型参数有较大的影响,故由上述方法确定Pasternak模型参数,可以消除荷载尺寸和形状对模型参数的影响,更好地反映管棚预支护体系的受力特性
(2)掌子面附近模型参数的变化
对管棚的力学模型分析来说,土体基床系数k的分布形式、取值大小对管棚的受力和变形情况影响很大。而在目前的研究中,整个隧道未开挖段均被简单地看作常基床系数下的弹性地基模型(双参数模型)来考虑。实际上,掌子面在上覆荷载作用下,必然由于水平约束不足而产生水平变形,从而导致掌子面附近范围内土体基床系数小于该范围外的值,这对管棚的受力是不利的[2]。下面将针对常基床系数下管棚力学模型的这一缺陷,结合掌子面前方未开挖段土体与管棚相互作用的实际情况,建立考虑掌子面水平位移影响的基床系数分析模型,研究掌子面前方土体的基床系数变化规律。
计算模型下边界固定,上边界施加分布荷载,侧边界留出一定高度的自由段,来模拟开挖掌子面,其余高度约束其水平向位移,如图2所示(仅显示左半部分)。
确定各点基床系数k值关系为:
k=p/s
(6)
式中:k ——基床系数,MPa/m;
p ——地基土所受压应力,MPa;
s ——地基的变位,m。
根据计算结果,绘制不同泊松比和开挖高度下的基床系数k沿隧道纵向的分布曲线如图3所示。
结果显示:基床系数在自由面处最小,沿隧道纵向逐渐增大,在约1倍自由面高度处趋于稳定。当泊松比μ及开挖高度h不同时,基床系数k的变化形式基本一致,只是基床系数稳定值k0及基床系数最小值与稳定值之比kmin/k0不同。
分别计算不同μ,不同h时kmin/k0的值,对结果进行拟合,可得kmin/k0随μ和h变化的函数:
kmin/k0=f(h,μ)k0=(1-0.9384μ2log(h+1))
(7)
将拟合结果与数值模拟分析结果对比,二者吻合较好,符合要求,按照拟合结果绘制kmin/k0随μ和h的变化图,如图4所示。
为简化计算,将基床系数沿隧道纵向变化的规律简化为如图5所示折线模型,并得到基床系数沿隧道纵向变化的表达式:
(8)
d=htan(π/4-φ/2)
2 管棚的力学模型建立
2.1管棚力学模型建立的基本假设
要想真实地反映管棚的受力和变形特点,揭示各种因素对管棚预支护效果的影响,模型必须建立在能够正确描述围岩条件、支护结构等因素影响的假设上。基于以上的研究并总结前人成果,本文的模型在以下基本假设的基础上建立[3]:
(1)承受管棚荷载的围岩为各向同性的连续介质,且符合Pasternak模型假设,其模型参数按照第1节所述确定;
(2)管棚构件的弯曲性态用Bernoulli-Euler梁理论来描述,忽略水平向应力的影响;
(3)将管棚与钢架的连结端视为有一已知竖向位移的固定端,且考虑初期支护的延滞效应,固定端取在第一榀与上一榀钢架的中间位置;
(4)长管棚在施工中是一次穿越,不考虑管棚间搭接。
2.2力学模型的建立
隧道开挖过程中管棚的力学模型分为以下两类:
类型一:当隧道开挖面距管棚前端较远时,开挖影响尚未达到管棚前端,此时管棚可看作半无限长的地基梁,如图6(a)。
类型二:当隧道开挖面接近管棚前端时,将管棚看作有限长度的地基梁,如图6(b)。
2.3微分方程求解
结合前面各节所得结论,由弹性地基梁理论可得管棚的挠曲微分方程。
(1)类型一
AB区段:
(9)
BC区段:
(10)
CD区段:
(11)
不同区段的微分方程通解为:
AB区段:
(12)
BC区段:该区段微分方程为四阶变系数常微分方程,考虑该方程求解的复杂性,可将该阶段基床系数的变化近似为n段逐渐变化的阶梯函数,从而使该变系数微分方程简化为若干段常系数微分方程,当n的取值足够大时,便可满足求解的精度要求。此时,第i段阶梯函数所对应的常微分方程通解为:
(13)
CD区段:
ω3(x)=eαλx(A3cosβλx+B3sinβλx)+e-αλx(C3cosβλx+D3sinβλx)
(14)
其边界条件为:管棚与钢架连结端既A点为有一已知竖向位移的固定端,其挠度ω(A)=ω0,转角ω(1)(A)=0;管棚前端既D点在开挖影响范围之外,挠度ω(D)=0,转角ω(1)(D)=0;其余管棚各边界点,截面两端挠度(ω(x)),转角(ω(1)(x)),弯矩(-EIω(2)(x)),剪力(-EIω(3)(x))均相等。
(2)类型二
在类型二中,AB区段与BC区段的微分方程及其通解和类型一相同。其边界条件为:管棚与钢架连结端既A点为有一已知竖向位移的固定端,挠度ω(A)=ω0,转角ω(1)(A)=0;管棚前端既C点为自由端,弯矩-EIω(2)(C)=0,剪力-EIω(3)(C)=0;基于管棚各边界点,截面两端挠度(ω(x)),转角(ω(1)(x)),弯矩(-EIω(2)(x)),剪力(-EIω(3)(x))均相等。
结合各段通解和边界条件,使用数学软件Mathematica可求解各待定系数,带入各式即可得管棚的挠度方程。
以上为仅在单次开挖条件下管棚的变形。由于土体沉降的不可逆性,管棚在隧道每一步开挖时所引起的变形都会逐步积累。所以,隧道开挖过程中每一步的总挠度都是之前各步开挖所引起的管棚变形之和,其表达形式为:
(15)
式中:ωi,m——管棚上第i点在第m步开挖时的总挠度,mm;
ωi,j——管棚上第i点在第j步开挖时所引起的挠度,mm。
2.4管棚力学行为的分析
在求得管棚挠度之后,可由以下各式解得管棚的转角、弯矩、剪力,由式(6)求得地基反力。
(16)
(17)
(18)
下边将以上节所求的管棚受力和变形方程为基础,分析管棚作用的力学机制。取以下工程数据:土方开挖前施做长管棚预支护,长管棚选用直径159mm,壁厚6mm的热轧无缝钢管,间距40cm,管内注M25水泥砂浆;围岩弹性模量E=20MPa/m,泊松比μ=0.40,重度γ=18.5kN/m3;隧道埋深H=5m,开挖高度h=8m,开挖步距s=2.4m;管棚与钢架连结端A点的初始竖向位移ω0=5mm。
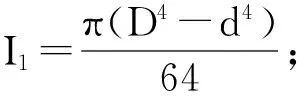
(19)
计算可得管棚挠度曲线及受力情况如图7(a)(b)所示(以格栅与管棚连结端为纵向位置0点):
由计算结果可知:(1)管棚的最大挠度和弯矩均发生在开挖面后方靠近开挖面处,说明管棚在隧道已开挖但尚未施作初期支护的位置处于最不利状态,是隧道开挖最危险的区域;(2)常基床系数时管棚的最大挠度为 13.39mm,最大弯矩为31.72kN·m,但考虑土体基床系数变化后,最大挠度达到14.65mm,最大弯矩达到34.25kN·m,分别相对超出9%、8%,且考虑土体基床系数变化后,其挠度及弯矩曲线有一定的延后,最大值位置更加靠近掌子面。所以,为了正确评估隧道开挖时管棚的变形和受力,在对管棚的力学分析中考虑掌子面开挖引起的基床系数变化很有必要。
3 结论
(1)掌子面前方岩土体的基床系数并非常数,而是沿着隧道开挖方向逐渐增大,且到一定距离后逐渐趋于稳定; 随土体泊松比和掌子面开挖高度呈二次抛物线变化,泊松比越大,开挖高度越高, 越小。
(2)分析管棚力学机制过程中,考虑掌子面水平变形引起的变基床系数后,更符合实际受力情况,能较好地反映管棚在隧道开挖过程中的真实力学行为。
[1]董军,彭立生.双参数地基模型研究及基础梁计算[J].武汉水利电力学院学报,1991,24(4):427-438.
[2]郑俊杰,章荣军,杨庆年. 浅埋隧道变基床系数下管棚的力学机制分析[J]. 岩土工程学报,2009,31(8):1 165-1 171.
[3]贾金青,王海涛,涂兵雄,等. 管棚力学行为的解析分析与现场测试[J].岩土力学,2010, 31(6):1 858-1 864.
Mechanical mechanism of piperoofs based on the pasternak model with variable coefficient of subgrade reaction
LUXinjian
(Fujian Academy of Building Research ,Fuzhou 350000)
In order to improve the elastic foundation beam model for pipe roofs with constant coefficient of subgrade reaction, the distribution law of coefficient of subgrade reaction in front of the excavation face is discussed.Furthermore, an analytical approach based on Pasternak elastic foundation beam theory with variable coefficients of subgrade reaction for pipe roof reinforcement was put forward,and the differential equations of corresponding deformations, turn angles, bending moments and shear were deduced.The results show that if take the lateral deformation effect of excavation face into account during the analysis, can gives more accurate calculation and is proved to be a better way to understand the reinforcement mechanism and improve design practice.
Tunnel; Pipe roof reinforcement; Variable coefficient of subgrade reaction; Pasternak elastic foundation beam; Mechanical mechanism
卢新建(1990.07-),男,助理工程师。
E-mail:1497918149@qq.com
2016-04-13
TU4
A
1004-6135(2016)06-0058-05

