Optimal design of near-Earth asteroid sample-return trajectories in the Sun-Earth-Moon system
Shengmao He·Zhengfan Zhu·Chao Peng·Jian Ma· Xiaolong Zhu·Yang Gao
RESEARCH PAPER
Optimal design of near-Earth asteroid sample-return trajectories in the Sun-Earth-Moon system
Shengmao He1,2·Zhengfan Zhu2,3·Chao Peng1·Jian Ma1,2· Xiaolong Zhu1,2·Yang Gao1
©The Chinese Society of Theoretical and Applied Mechanics;Institute of Mechanics,Chinese Academy of Sciences and Springer-Verlag Berlin Heidelberg 2015
In the 6th edition of the Chinese Space Trajectory Design Competition held in 2014,a near-Earth asteroid sample-return trajectory design problem was released,in which the motion of the spacecraft is modeled in multi-body dynamics,considering the gravitational forces of the Sun,Earth,and Moon.It is proposed that an electric-propulsion spacecraft initially parking in a circular 200-km-altitude low Earth orbit is expected to rendezvous with an asteroid and carry as much sample as possible back to the Earth in a 10-yeartimeframe.TheteamfromtheTechnologyandEngineering Center for Space Utilization,Chinese Academy of Sciences has reported a solution with an asteroid sample mass of 328 tons,which is ranked first in the competition. In this article,we will present our design and optimization methods,primarily including overall analysis,target selection,escape from and capture by the Earth-Moon system,and optimization of impulsive and low-thrust trajectories that are modeled in multi-body dynamics.The orbital resonance concept and lunar gravity assists are considered key techniques employed for trajectory design.The reported solution,preliminarily revealing the feasibility of returning a hundreds-of-tons asteroid or asteroid sample,envisions future space missions relating to near-Earth asteroid exploration. KeywordsNear-Earthasteroid·Sample-returntrajectory· Space trajectory design competition·Orbital resonance· Lunar gravity assist
1 Introduction
The6theditionoftheChineseSpaceTrajectoryDesignCompetition held in 2014 was organized by the Chinese Society of Theoretical and Applied Mechanics and the State Key Laboratory of Astronautic Dynamics.Following the tradition of the past editions,participating teams are required to design extremely complex flight trajectories for an innovative space mission in a two-month time frame.In the year of 2014,a challenging trajectory design problem for a near-Earthasteroid(NEA)sample-returnmissionwasreleasedon July 15.The most significant uniqueness of this problem is thatthespacecraft’smotionissupposedtobesimultaneously influenced by the gravitational forces of the Sun,Earth,and Moon.Asfarasweknow,trajectorydesignusingmulti-body dynamics might be much more difficult than that using the patched-conic model,which is employed for proposing all the problems in the past editions and even in all the editions of the worldwide Global Trajectory Optimization Competition(GTOCs)[1].Therefore,the trajectory design problem in the 6th edition to be described in the subsequent section is obviously a milestone in the development process of the trajectory design competitions.
A spacecraft parking in a circular 200-km-altitude low Earth orbit is expected to rendezvous an NEA that will be selected among a total of 791 potential targets.The spacecraftwillstayonanasteroidforatleast30daysforasampling operation,and then carry asteroid samples back to the Earth. The total mission duration is limited within 10 years andthe mission’s starting time window is between January 1,2021(MJD59215)and December 31,2030(MJD62867). The inclination of the parking orbit,which is referenced in an Earth-centered inertial coordinate frame(its XY plane is selected to be the ecliptic plane),is set to be within 20◦-90◦. The right ascension of ascending node and the true anomaly of the parking orbit can be arbitrarily chosen.The samplereturn trajectory ends up with Earth atmospheric reentry at the altitude of 200 km and the reentry velocity must be no more than 11 km/s.The initial mass of the spacecraft is 2 tons and the propellant mass is 1.5 tons.The spacecraft is assumed to be propelled by electric propulsion with the specific impulse of 3000 s and the thrust amplitude in the range of 0-10 N.The thrusting direction could be arbitrarily directed.It is noted that the proposed configuration of the propulsion system has not been validated by practical engineering.The allowable minimum ranges from the spacecraft to the Earth and the Moon are set to be 6578 and 1838 km,respectively.The spacecraft’s motion is influenced simultaneously by the gravitational forces of the Sun,Earth,and Moon,and the motion of an asteroid is assumed to follow a simplified heliocentric Keplerian elliptical orbit.The performance index of trajectory design is to maximize the mass of the asteroid sample carried back to the Earth.
Inthepastdecade,explorationofminorbodiesinthesolar system(asteroids and comets)has been a fascinating topic in space science research.Among numerous minor bodies,NEAsareeasiertoaccessthantheothers.Anynewscientific discovery of NEAs is thought to be beneficial for us to gaining deeper understanding of the origin and evolution of the solar system.Besides,we might have other motivations for NEA exploration.As far as we know,more and more potentially hazardous NEAs are being discovered.These NEAs’orbits cross the Earth revolution orbit about the Sun,posing unforeseen impact threats to the Earth.Therefore,proposing strategies for deviating the orbits of these small bodies is quite urgent.On the other hand,asteroids may contain resources that are scarce on the Earth,and bringing these resources back to the Earth is promising in the near future[2].NEAs are also related to manned spaceflight.Human’s landing on NEAs might be a good step-stone for the manned flight to the Mars.There is another scheme of the manned NEA mission scenario,in which a total or a part of a NEA is captured and redirected to an Earth orbit or a lunar orbit and then a manned spacecraft is launched to land on this asteroid.This is the main content for the“asteroid redirect mission”recently proposed by NASA.Some researches on this topic have appeared.For example,Brophy et al.[3]proposed the mission for retrieving asteroids,and Sanchez[4]categorized a class of retrievable asteroids,which can be captured into the Sun-Earth L1 and L2 with a total of velocity impulses no more than 500 m/s.In addition,Neus et al.[5]addressed the feasibility of capturing small NEAs into the vicinity of the Sun-Earth L2 using a continuous-thrust propulsion system assumed to be attached to the asteroid,and listed the candidate NEAs to be captured.Other representative research work on capturing an asteroid can be found in Refs.[6-8].Whatever we propose as NEA explorationmissions,thereareseveralfundamentalquestionstobe answered:how to select asteroid target,how to rendezvous asteroids,how to deviate their orbits or capture them back to theEarth-Moonsystem,etc.?Allthesequestionsareclosely related to design and optimization of spaceflight trajectories.
Because the spacecraft flying toward NEAs are significantly influenced by the gravitational forces of the Sun,Earth,and Moon simultaneously,the research on trajectory design using multi-body dynamics for an NEA exploration missionshasattractedourattentioninthepastdecade,which emphasizes designing low-energy transfer trajectories by fully making use of multiple gravitational forces.As we knowsofar,Venus,Mars,andEarthcouldbeusedforgravity assisttoreducefuelconsumptionforinterplanetaryflightsto NEAs.Meanwhile,lunar gravity assists might play important roles in fuel-optimal escape from and capture by the Earth-Moon system,thus providing insight for designing low-energy transfers between geocentric orbits and NEAs. The traditional analysis of gravity assist is based on the patched-conic model,in which the third-body gravitation occursattheflybytimeinstantonly.Thecontinuouseffectof the third-body gravitation(usually caused by the moons in a planetarysystem)hasbeenalsostudied[9].Whenthespacecraft periodically encounters the third body(for example the Moon),thespacecraftisdeemedtomoveinamoonresonance orbit.This design strategy was employed for analyzing the orbitalperiapsisraisingoftheESASmart-1[10].Also,Campagnola and Russell[11]used the resonance orbit concept to design the trajectories with cheap insertion maneuvers into the moons’science orbit in the Jovian and Saturnian systems.Meanwhile,Cuartielles et al.[12]and Alessi et al.[13]have conducted studies on the semi-major axis,eccentricity,and inclination of resonance orbits in the circular restricted three-body dynamics,which is used to design the asteroid retrievingmissions.Theserepresentative researches indicate that the orbital resonance concept is a useful tool for designing low-energy transfer trajectories.
Trajectory design in multi-body dynamics is challenging and currently no versatile methods are found in the existing literature.A designer must conduct detailed analysis for trajectory design,which usually depends on designer’s understanding of the flight mechanics in multi-body dynamics.Inthisarticle,wewillpresentourstrategiesfordesigning the NEA sample-return trajectory,primarily including overall analysis,target selection,escape from and capture by the Earth-Moonsystem,andoptimizationofimpulsiveandlowthrust trajectories that are modeled in multi-body dynamicsin this article.Lunar resonance orbits are employed to make use of lunar gravity assists,which is a highlight of our effortstodesignlow-energytransfertrajectories.Theremainder of the article is organized as follows.In Sect.2,the dynamical model of the spacecraft and overall analysis of its flight trajectory are presented.In Sect.3,the methods for asteroid target selection are described.Section 4 presents the orbital resonance concept and its application for designing trajectories of escape from and capture by the Earth-Moon system.Section 5 presents a near-optimal steering scheme for low-thrust orbital raising.In Sect.6,the techniques for converting velocity impulses into lowthrust arcs are described.The trajectory design solution and the conclusions are given in Sects.7 and 8,respectively.
It is noted that our attention is focused on presenting our design methodology and routine numerical techniques are not described in detail.As a result,the specific data of trajectory solutions at intermediate steps might be hard to exactly duplicate by independent attempts for solving the problem because a number of sophisticated numerical techniques might be implemented by different subroutines,algorithms,and the relevant parameter setup,which are trivial to be enumerated herein.However,it is no doubt that the proposed methods,following which the solution with a similar design performance index could be obtained,shed light on interpreting the flight mechanism designed for carrying back hundreds-of-tons asteroid sample.
2 The dynamical model and overall analysis of flight trajectories
Considering the gravitational forces of the Sun,Earth,and Moon,the equation of motion for the spacecraft is modeled by a restricted four-body(Sun,Earth,Moon,and spacecraft)dynamics in an Earth-centered ecliptic inertial reference frame(see xEyEzEas shown in Fig.1):
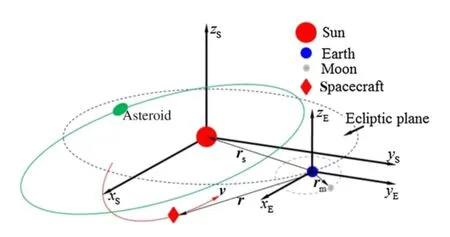

where the spacecraft’s position and velocity vectors are r=[x y z]Tand v=[˙x˙y˙z]T,and μe,μs,and μmare the gravitational parameters of the Earth,Sun,and Moon,respectively.The position vectors of the Sun and the Moon in the Earth-centered inertial coordinate frame are denoted by rsand rm,respectively,which are computed from a given ephemeris presented in the Appendix.The spacecraft mass,thrust amplitude,and the unit vector of thrust direction is denoted by m,F,and α,respectively.The time rate of the spacecraft mass is formulated as

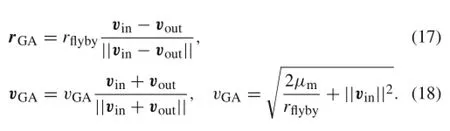
where ge(ge=9.80665 m/s2)is the sea-level acceleration and Ispisthespecificimpulseofthepropulsionsystem(Isp= 3000 s).The illustration of the asteroid motion in the Sun-Earth-MoonsystemisdepictedinFig.1.Theasteroidmotion follows a heliocentric Keplerian elliptical orbit referenced in the heliocentric coordinate frame xSySzS,which is assumed to be parallel to xEyEzE.When the spacecraft stays on the asteroid,its motion remains the same as that of the asteroid. Once the spacecraft leaves the asteroid,it carries an asteroid sample;and therefore,the total mass of the spacecraft has an instantaneous increment of sample mass.
Currently,therearenomaturesystematicmethodsfortrajectory design in the restricted four-body dynamical system(or the Sun-Earth-Moon-spacecraft system).For the NEA sample-return flight trajectories,the gravities of the Sun,Earth,and Moon have variable influences on the spacecraft’s motion at its different flight phases.This fundamental characteristic makes the problem more complicated to solve,and it is very likely that participating teams employ different design strategies to obtain different results.The comparison of these results is an important means for promoting our understanding of advanced techniques of trajectory design and optimization using multi-body dynamics.The following content in this section reflects our overall analysis of designing the NEA sample-return trajectories.
In order to reduce the complexity of trajectory design,a logical approach is to divide the flight trajectory into a number of segments.These segments should be patched together eventually.Based on our understanding of spaceflight mechanics,we divided the whole trajectory into four segments:(1)from the low Earth parking orbit to the first lunar flyby;(2)from the lunar flyby to asteroid rendezvous;(3)asteroid departure to lunar flyby;(4)from the last lunarflyby to Earth atmospheric reentry.These four segments are illustrated in Fig.2.The connection of the 1st and 2nd segments and the connection of the 3rd and 4th segments are both implemented using lunar resonance orbits(see details in Sect.4).We then assumed that a Hohmann transfer from the low Earth parking orbit to the Moon is employed for the 1st segment,and the required velocity impulses are easily computed.For the 4th segment,according to the reentry velocity constraint,it is estimated that the spacecraft could be placed in an Earth-centered highly elliptical orbit with the reentry speed at 11 km/s(at 200 km altitude)in terms of two-body dynamics.In this elliptical orbit,the spacecraft velocity relative to the Earth is 1.37 km/s when it crosses the lunar orbit.Therefore,if the spacecraft encounters the Moon with a proper velocity level,it might implement atmospheric reentry without exerting extra velocity impulses.
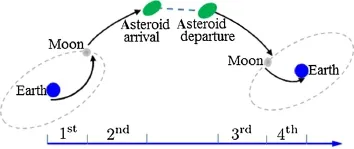
Fig.2 Illustration of the pre-defined four segments for constructing asteroid sample-return trajectories
According to the above-mentioned trajectory segmentationandourknowledgeoftrajectorydesignandoptimization,we then figured out the following guidelines for detailed design,and they are concerned with three aspects:target selection,escape from and capture by the Earth-Moon system,andoptimizationofimpulsiveandlow-thrustmaneuvers.
(1)Low-energy flight trajectories are desired so that the spacecraft may carry as much sample as possible.In order to implement low-energy flight,the heliocentric orbit of the potential target should be close to that of the Earth.If we consider that the time interval between two consecutive Earth’s closest encounters with an asteroid should be less than 10 years,a large number of asteroids can be excluded.
(2)Lunar gravity assists might provide considerable velocityimpulseswithoutconsumingpropellant.IntheEarthcentered coordinate frame,if the spacecraft cannot escape from or be captured by the Earth-Moon system via a single lunar flyby,the spacecraft might be inserted into lunar resonance orbits.In this way,the spacecraft is able to re-encounter the Moon and use the lunar gravity assist for the second time.The lunar resonance orbit is useful to patch the trajectory segments in the interplanetary space and in the Earth-Moon system.
(3)All trajectory segments are designed using velocity impulses as orbital maneuvers at the first step except the one of orbital raising from a low Earth orbit using low thrust.After we obtain the trajectory solution with impulsive thrust,velocity impulses are then converted into low thrust orbital arcs.
Infact,thecollinear point periodic orbitsand their associated invariant manifolds in the restricted circular three-body dynamics provide an effective tool for designing flight trajectories modeled in multi-body dynamics.The theory of invariant manifolds associated with halo orbits apparently can be used for trajectory design and also for solving the proposed problem in this competition.However,we speculated that the trajectory design solely depending on invariant manifolds might not result in a globally optimal solution(this statement is based on our knowledge only and is not a validated conclusion).In addition,in order to obtain new understanding of the flight mechanics in the Sun-Earth-Moonsystem,weemployedlunarresonanceorbits(or multiple lunar gravity assists)for solving the NEA samplereturn trajectories,instead of using invariant manifolds.
3 Searching the asteroid target in terms of design performance index
We need to select one asteroid for sample-return among a total of 791 candidate targets,which requires an effective approach for asteroid target screening.First,we made a simple analysis for estimating the design performance index.Subsequently,we proposed a numerical computation and optimization process for further target screening.This process is divided into three steps:(1)grid search with the Lambertalgorithmfortheasteroid-EarthandEarth-asteroid trajectorysegmentsmodeledusingtheheliocentrictwo-body dynamics;(2)the solution in the two-body dynamics is placed in the restricted four-body dynamics and optimized with multiple-impulse orbital maneuvers;(3)continuation on the asteroid departure time instants for locating potential global optimum in the restricted four-body dynamics.The first step is described in Sect.3.2 and the second and third steps in Sect.3.3.
3.1 Simplified estimation of the design performance index
As described in Sect.2,the whole trajectory is divided into four segments.The total velocity impulses for each of these four segments are denoted by Δv1,Δv2,Δv3,and Δv4,respectively.Forthe1stsegment,theHohmanntransfer is used for approximately computing the required velocity impulses of the transfer from the low Earth orbit to theMoon.We then assumed that the spacecraft would fly into interplanetary space via one or more times lunar flybys. Therefore,only the velocity impulse required for departing the low Earth orbit is needed and no velocity impulse is needed for rendezvousing with the Moon,which results in Δv1=3.24 km/s for the 1st segment.For the 4th segment,weassumedthatnovelocityimpulseisneeded(Δv4= 0 km/s)by considering that the capture could be achieved usinglunargravityassists.Itisnotedthatfullytakingadvantages of lunar gravity assists for escape from and capture by the Earth-Moon system is a key technique in our design strategy that results in our assumptions for estimating Δv1and Δv4,and these assumptions are finally validated by the designed solution.
Therefore,other velocity impulses required are counted in the 2nd and 3rd segments.As a result,the total required velocity impulses for the 2nd and 3rd segments determine the design performance index,thus providing a principle for asteroid target selection.We proposed a simple equationtoapproximatelycalculatethedesignperformanceindex(J in Eq.(3),the asteroid sample mass)that is modeled as follow

where m0(=2 tons)is the initial spacecraft mass,m1is the spacecraft mass at asteroid arrival,and mf(mf=0.5 tons if 1.5-tons propellant is consumed)is the spacecraft mass at Earth atmospheric reentry.It is noted that mf+J=(m1+ J)c0leads to Eq.(3).Considering that Δv1=3.24 km/s and Δv4=0 km/s,the contour of J(in kg)about Δv2and Δv3are plotted in Fig.3.
As shown in Fig.3,taking the contour of J=300000 kg as an example,the contour’s ratio in Δv2and Δv3is about 1:200.Thisfactindicatesthatthe3rdsegmentfromtheasteroid to the Moon is the key segment,and as fewer velocity impulses as possible are desired,which ensures as much asteroid sample as possible to be carried back.Therefore,we focus our attention on designing this segment with more effort and on the 2nd segment from the Moon to the asteroid with less effort.
3.2 Searching asteroid target using the Lambert algorithm
In the heliocentric two-body dynamical model,the transfer from the Earth to the asteroid is considered(the Moon and the Earth are assumed to be the same point).For the Earth-to-asteroid segment,we assume that Earth departure occurs at t1with Δv2,1exerted and asteroid arrival at t2with Δv2,2.For the asteroid-to-Earth segment,we assume that asteroid departure occurs at t3with Δv3,1exerted and Earth arrival at t4with Δv3,2.In this way,the 2nd and 3rd segments described in Fig.2 are then illustrated in details by Fig.4.
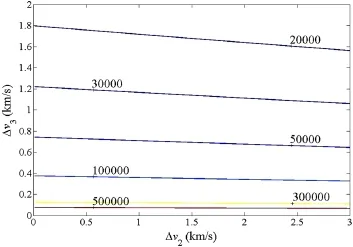
Fig.3 The contour of the design performance index with respect to Δv2and Δv3

Fig.4 Illustrationofthe2ndand3rdsegmentsintheheliocentrictwobody dynamical model
Wefirstdevisedagridsearchoft3andt4usingtheLambert algorithm for the first step of asteroid target screening.The Lambert algorithm with multiple orbits(N=1,2,3,4 where N denotes the number of orbits,and for each N there are two branches of Lambert solutions)are utilized to compute the total velocity impulses(Δv3=||Δv3,1||+||Δv3,2||). The time interval of t3and t4is set to be 5 days,and the search domains of t3and t4(both in days)are defined to be
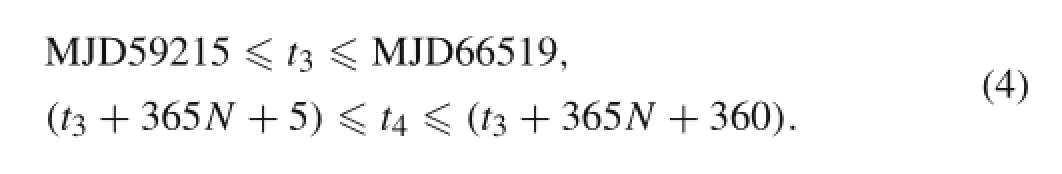
The solution pruning condition is set to be

It is noted that the empirical values for defining time domainsandsolutionpruningarelooselysetsuchthatpoten-tial targets will not be omitted at the expense of some unnecessary computation(the same case applied for the following Earth-to-asteroid segment).Also,if||Δv3,2||is set to be a large value(4 km/s),the spacecraft might not be captured by the Earth-Moon system with one or two lunar gravity assists only.
Based on the searching results of the asteroid-to-Earth segment,the Earth-to-asteroid segment is searched using the similar approach.Considering the minimum stay time on an asteroidof30days,theLambertalgorithmisemployed(N= 1,2,3,4)to calculate the total impulses(Δv2=||Δv2,1||+ ||Δv2,2||).For a set of solution of specific values of t3and t4,the search domains of t2and t1(both in days and the time interval of t2and t1is set to be 5 days)are set to be

The solution pruning condition is set to be

ThegridsearchresultsareshowninTable1(“2003SM84”is the final selection but is not ranked first in this step).At this step,there are 39 targets and more than 2000 trajectories are remaining,which are then considered to be a set of candidate solutions.However,the two-body dynamics is not accurate enough for target selection,but used as a preliminary screening process.The solutions in Table 1 will be optimized with multiple-impulse maneuvers in the restricted four-body dynamics,which is presented in the subsequent Subsection.
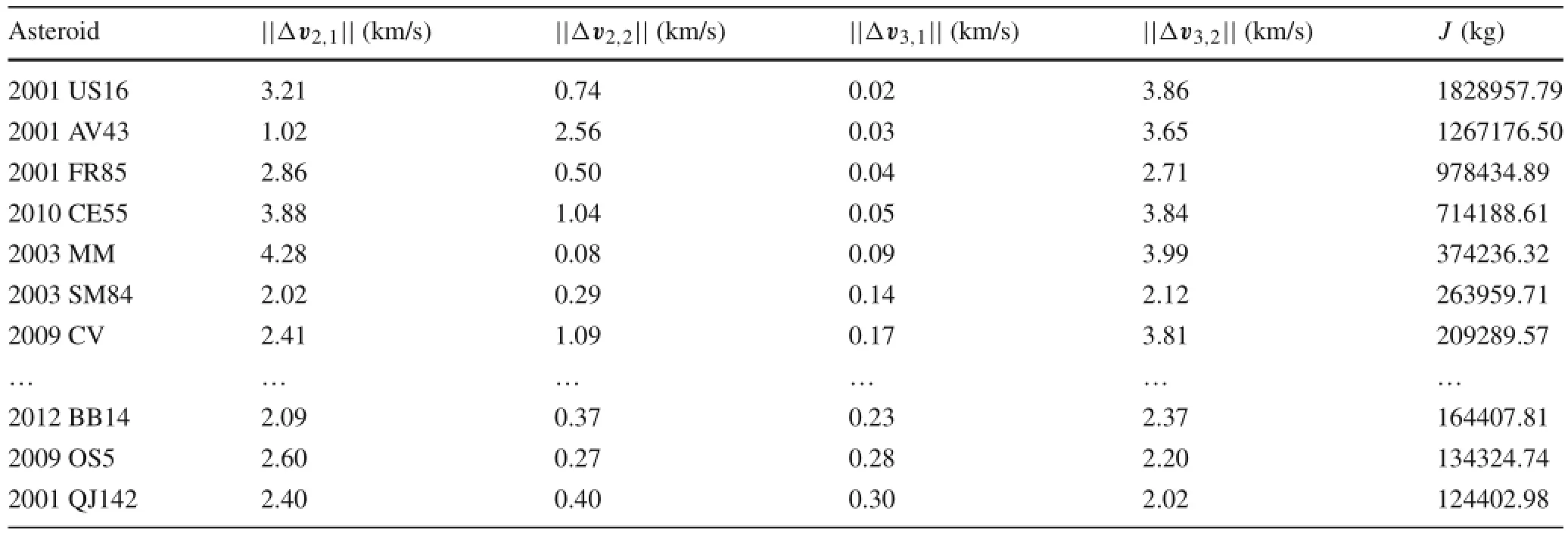
Table 1 The velocity impulses exerted and the design performance index
3.3 Trajectory optimization with multiple-impulse maneuvers and a continuation technique
ThegridsearchusingtheLambertalgorithminthepreceding Subsection does not consider whether the spacecraft could be captured by the Earth-Moon system using lunar gravity assists.In addition,the multiple-impulse instead of the two-impulse orbital maneuver might be useful to reduce the totalvelocityimpulses,especiallyformultiple-orbitLambert solutions.Therefore,we devised a trajectory optimization procedure for solving multiple-impulse transfer problems modeled in the Sun-Earth-Moon system using the solutions given in Table 1 as the initial guess.In this procedure,the asteroid-to-Moon and Moon-to-asteroid trajectory segments(correspondingtotheEarth-to-asteroidandasteroid-to-Earth segmentsinSect.3.2)aretobeoptimizedusingadirectoptimization method.
For the asteroid-to-Moon segment(corresponding to the 3rd segment in Fig.2),the asteroid departure date is denoted by τ0(the initial value of τ0is t3)and a departure impulse is Δvτ0(theinitialvalueofΔvτ0issettobeΔv3,1).TheMoon’s arrival date is τf(the initial value of τfis t4).We empirically allocated six time nodes(τ1,τ2,...,τ6)equally spaced into the time interval from τ0to τf,and the velocity impulse at eachnodeisassignedtobeΔvτ1,Δvτ2,...,Δvτ6(theinitial values are all set to be null).It is noted that the number of velocity impulses is empirically selected and optimization of multiple impulses in the restricted four-body dynamics is still a challenging problem that deserves further study.
At Moon’s arrival,let us define the spacecraft position and velocity vectors to be r(τf)and v(τf),respectively,and the Moon’s position and velocity vectors to be rm(τf)and vm(τf),respectively.In order to avoid the singularity resultingfromtrajectorynumericalintegrationwhentheconstraint r(τf)=rm(τf)is satisfied,the Moon’s gravitation is not counted(μm=0 in the Eq.(1))in the preceding 0.4 days
(an empirical value)of lunar encounters.At lunar flyby,the relative velocity is computed as

The lunar gravity assist is modeled as a rotation of vn(τf),which rotates about the vertex of vm(τf)with an angle δ to obtain the relative velocity after lunar flyby(the corresponding illustration is presented in Fig.7).The rotation angle δ is computed by
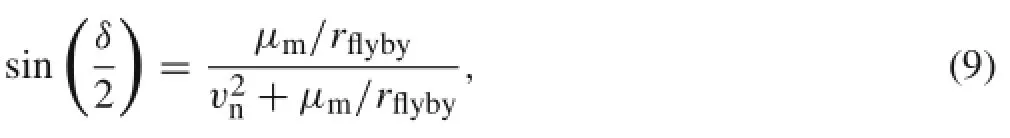
where rflybyis the orbital radius of the spacecraft relative to theMoonatthelunarclosestapproach,vnistheamplitudeof lunarrelativevelocity(vn=||vn||)atlunarflyby.Theorbital energy after lunar flyby referenced in the Earth-entered inertial frame is approximately computed as

For the Moon-to-asteroid segment(corresponding to the 2nd segment in Fig.2),the same analysis are conducted. Considering the inverse flight in time,the asteroid arrival date is denoted by τf(the initial value of τfis set to be t2)and an impulse exerted at asteroid arrival is Δvτf(the initial values of Δvτfis Δv2,2).The Moon’s departure date is τ0(the initial value of τ0is t1),and the orbital energy before lunar flyby(following the same computation in Eq.(10))is denoted by E(τ0).
We finally set up trajectory optimization problems in the restricted four-body dynamical model with multipleimpulse orbital maneuvers,and they are transformed to be parameter optimization problems shown in Table 2,in which the Prob.(a)and Prob.(b)are corresponding to the asteroid-to-Moon and Moon-to-asteroid segments,respectively.The design performance index is to minimize the total velocity impulses of each segment.The nonlinear parameter optimization problems are solved by using the subroutine“fmincon.m”in MATLAB.
Table 3 presents a part of multiple-impulse trajectory solutions obtained by solving the nonlinear optimization problems in Table 2,in which Δv2and Δv3represent the totalvelocityimpulsesrequiredforthe2ndand3rdsegments,respectively.By ranking Δv3(or J calculated by Eq.(3)),we finally chose the asteroid“2003 SM84”as the target for sample-return and its orbit is shown in Fig.5.

Table 2 The parameter optimization problems for the asteroid-to-MoonandMoon-to-asteroidtrajectorysegmentswithmultiple-impulse maneuvers
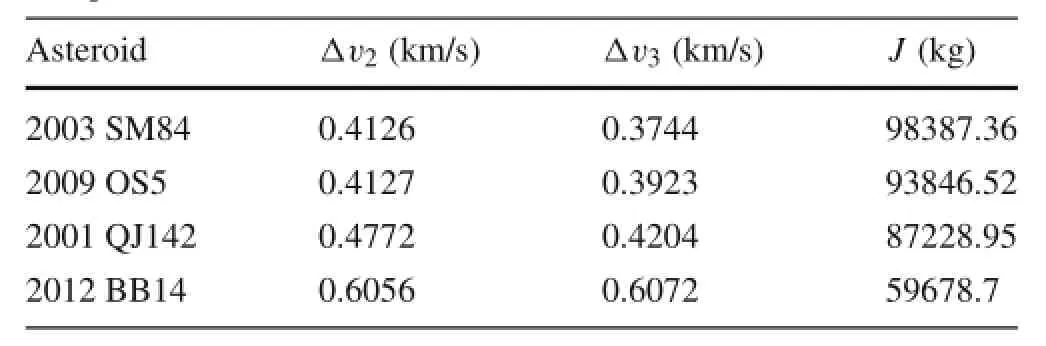
Table3 Thecandidateasteroidtargetsviasolvingparameteroptimization problems in Table 2
For the best multiple-impulse solution obtained via trajectory optimization(the target asteroid is“2003 SM84”),the asteroid stay time is 1415 days and the asteroid arrival and departure dates are 2028-08-01(MJD61984)and 2032-06-16(MJD63399),respectively.In order to improve the design performance index further,a continuation technique is employed to find a potential global optimum.This technique is simple and termed continuation on the time instants of asteroid departure.For the trajectory optimization of the 3rd segment given in Table 2,an additional velocity impulse(denoted byand its initial value is set to be null)is added at an earlier time instant(the initial value is set to be-60 days),and a new optimization problem modeled in Table 4 is set up and solved(rastand vastdenote the asteroid position and velocity vectors,respectively).In the results obtained,the velocity impulses that are less than 1 m/s are finally removed.
The same procedure is repeated by allocating a velocity impulse at the time instant(a new asteroid departure date)initially 60 days preceding the previous asteroid departure date,and a new optimization problem similar to that setup inTable 4 is solved and a new solution is then obtained.This procedurecontinuesuntiltheasteroiddeparturedateisearlier than 2028-08-31(MJD62014).In this way,we then obtained a series of transfer trajectories from the asteroid to the Moon with different asteroid departure dates.Via sorting all these solutions in terms of the total velocity impulses,the optimal asteroid departure date is finally selected to be 2029-10-01(MJD62137)thatcorrespondstotheminimaltotalvelocity impulses of 0.1037 km/s for the asteroid-to-Moon segment,which is a key solution for carrying as much sample as possible back to the Earth.In terms of this approach,the orbital states at lunar flyby of the 2nd and 3rd segments are presented in Table 5,which are used for analysis of the escape from and capture by the Earth-Moon system.
Fig.5 The asteroid orbit viewed in the a Heliocentric inertial frame and b Sun-Earth system rotating frame

Table 4 The new optimization problem for the spacecraft trajectory of the asteroid-to-Moon segment
4 Escape from and capture by the Earth-Moon system
4.1 Orbital resonance concept and simplified modeling
In celestial mechanics,orbital resonance is a fundamental concept,usually referring to the fact that some celestial bodiesfolloworbitalmechanicsinwhichtheirorbitalperiodsare related by a ratio of small integers.In this study,orbital resonance occurs between a spacecraft and the Moon.When the orbitalperiodofaspacecraftisinanintegerratiowiththatof the Moon,the spacecraft flies in a lunar resonance orbit.For simplicity and clearance,a resonance ratio in this article is defined as the ratio of the number of orbits completed in the same time interval.As a result,if the spacecraft completes p orbits and the Moon completes q orbits,the resonance ratio is p:q where p andq arepositiveintegers.Inthisstudy,lunar resonance orbits provide a useful approach for making use of multiple lunar gravity assists.
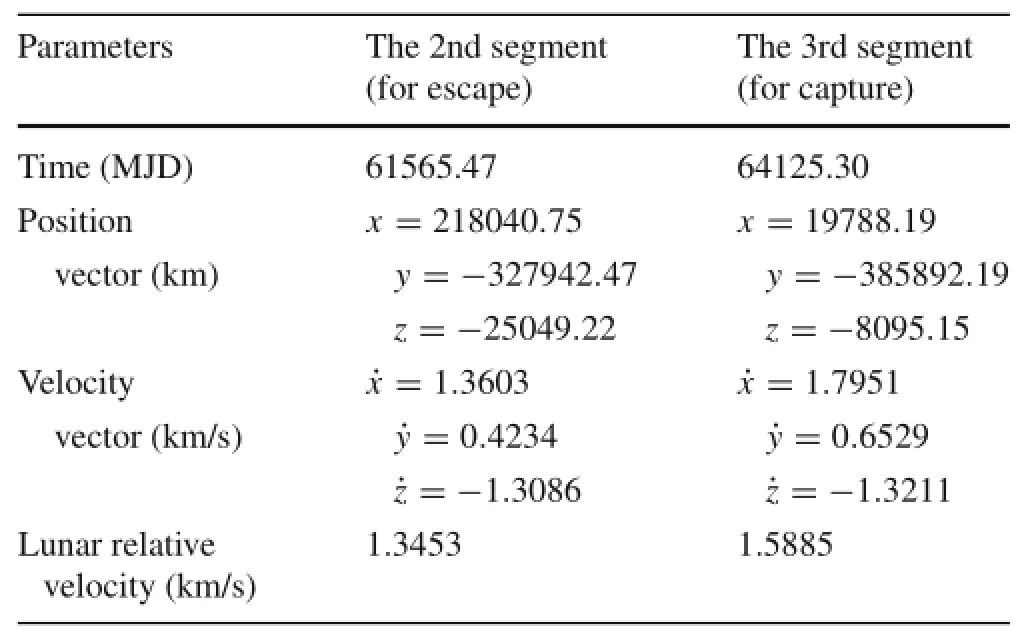
Table 5 The spacecraft orbital states at lunar flyby of the 2nd and 3rd segments(in the Earth-centered inertial coordinate frame)
The illustration of lunar gravity assist and orbital resonance is shown in Fig.6,in which the lunar position and velocity vectors are denoted by rmand vm,respectively,vnis the lunar relative velocity vector(before flyby),and v is the velocity vector of the spacecraft relative to the Earth.All these variables are evaluated in the Earth-centered coordinate frame.After lunar flyby,vnbecomesIn this way,thelunar gravity assist is modeled as an instantaneous velocity change via a rotation of vnabout the vertex of vmwith an angle of δ(see Eq.(9)).
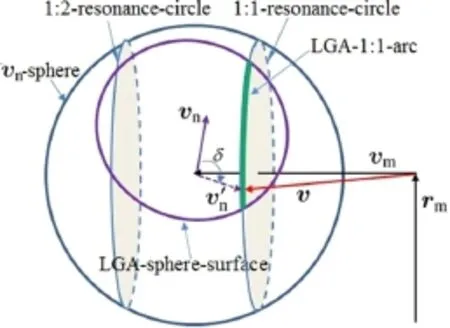
Fig.6 Illustration of lunar gravity assist
Forinterpretinglunargravityassists(LGA)andresonance orbits,wedefinedthefollowingdefinitionsforfurtheranalysis:
(1)vn-sphere:the origin of the sphere is the vertex of the lunar orbital velocity vector vm,and the sphere radius is the module of vn.
(2)LGA-sphere-surface:aportionofthevn-sphere’ssurface on which the vertex of v′nresides after rotating vnabout the vertex of vmwith an angle of δ.
(3)p:q-resonance-circle:the circle on the vn-sphere on which the module of v is a constant value that is correspondingtothe p:q resonanceratio(1:1-resonancecircleand1:2-resonance-circleinthefigureasexamples)and the normal of the circle is parallel to vm.
(4)LGA-p:q-arc:the crossing arc of the LGA-sphere surface and the p:q-resonance-circle.If v′nresides on this arc,the spacecraft will return to the Moon after p orbits(or q lunar orbits)in terms of the two-body dynamics.
Each lunar flyby is then related to a rotation of vn.If vnresides on the p:q-resonance-circle,the spacecraft may periodicallyflybytheMoonandthenperiodicallyexploitthe lunar gravitation.Therefore,the LGA-p:q-arc is a potential bridge to connect the current and target vn.If the spacecraft cannothoptothetargetvndirectlywithasingleLGA,itmay try to hop to a LGA-p:q-circular-arc at first and then hop to the target.In order to describe the rotation of vn,the SWT coordinateframeisintroduced,asshowninFig.7,wherethe W-axis is along the Moon’s velocity(j as the unit vector),the T-axis is perpendicular to the lunar orbit plane(k as the unit vector and k=rm×vm/||rm×vm||),and the S-axis is determined by the right handed principle(i as the unit vector).
The direction of vncan be expressed by two angular parameters ρ and σ that are computed as follows(also as shown in Fig.7)
where the domains of ρ and σ are defined as ρ∈[0,π]and σ∈[-π,π]in terms of the illustration in Fig.7.The parameter ρ is located in[0,π/2]if vn·j≥0 and in[π/2,π]if vn·j≤0(ρ=arccos(cosρ)+π),and the parameter σ is located in[0,π]if vn·k≥0 and in[-π,0]if vn·k≤0.It is noted that if ρ=0 or π,σ is undefined. Inversely,vncan be computed if||vn||,ρ,and σ are given.

Fig.7 Illustration of the vector vnand the parameters[ρ,σ](S′and T′are parallel to S and T,respectively)
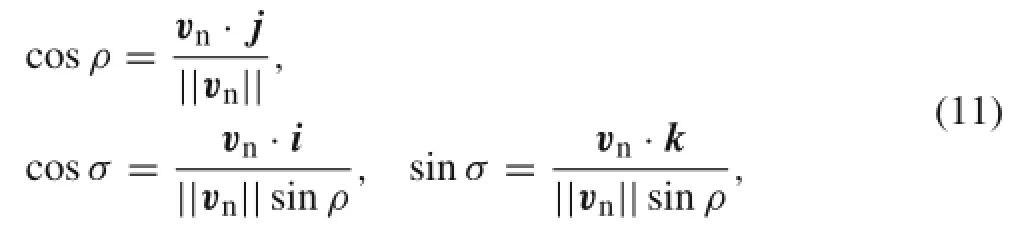
According to the definitions of ρ and σ,the p:qresonance-circle can be expressed by the parameter ρ. Assuming that the period of the lunar orbit is Pmand the resonance ratio is p:q,the period of the spacecraft orbit and the orbital energy in the Earth-centered reference frame are computed as
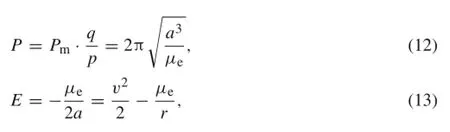
wherea isthesemi-majoraxisofthespacecraftorbit,r isthe orbital radius(r=||r||where r is the spacecraft’s position vector),and v is the velocity amplitude(v=||v||).In terms of the period and energy(see Eqs.(12-13)),the amplitude of velocity is calculated as

Consider the triangle encircled with vn,vm,and v,ρ is computed as follows in terms of the p:q resonance ratio

Once ρ is chosen,the upper and lower limits of σ are also determined with the corresponding LGA-p:q-arc.If vncan not turn to the target state directly,the lunar resonance orbit will be employed.In this way,vnfirst hop to a LGA-p:q-arc andthenhoptothetargetstate,andweexpectedthatthelunar resonanceorbitisabridgetoconnectthe1stand2ndsegment,and also the 3rd and 4th segments.Therefore,the design of lunar resonance orbit is converted to the determination of[ρ,σ].It is noted that all the analysis in this section are based on the two-body dynamics.
4.2 Escape with double lunar flybys
For the set of orbital states at lunar flyby of the 2nd segment given in Table 5,the parameters[ρ,σ]of vnis[69.75◦,-70.21◦]and||vn||=1.3453 km/s,which is corresponding to the lunar relative velocity just after escaping from the Earth-Moon system.A challenge to be tackled is that we need to design a transfer trajectory for the spacecraft from an Earth orbit to reach this set of orbital states using multiple lunar gravity assists.
First,let us consider vnjust before the first lunar flyby,which is corresponding to an Earth-centered elliptical orbit thatcrossesthelunarorbit.Consideringthattheamplitudeof vn(1.3453 km/s)at lunar flyby(MJD61565.47)is set to be equaltothatgiveninTable5,anoptimumsetof[ρ,σ]should be chosen in terms of the minimized apogee of the correspondingEarth-centeredellipticalorbit,whichshouldsatisfy thefollowingthreeconstraints:(1)theperigeealtitudeisconstrainedtobe200km.Thisconstraintispreparedforpatching the trajectory segment of low-thrust orbit raising from the 200-km-altitude low Earth orbit to a highly elliptical orbit whoseperigeealtitudeisalsocloseto200km;(2)theapogee should be no less than the Moon’s orbital radius,which is a necessary condition for using lunar gravity assist.However,the higher the apogee the more velocity impulses needed fordepartingthelowEarthorbit;(3)theorbitalinclinationis between20◦and90◦,whichistheproblemconstraint.Therefore,grid search of ρ and σ(0≤ρ≤π,-π≤σ≤π)is performed to find vnand the corresponding elliptical orbit,whichfinallyresultsin[ρ,σ]=[136.72◦,13.43◦]toexpress vn(||vn||=1.3453 km/s)before the first lunar flyby.
Next,wewilldeterminehow[ρ,σ]changefromtheinitial([136.72◦,13.43◦])tothetarget([69.75◦,-70.21◦]),andthe required rotation angle of vnis 100.41◦.In terms of Eq.(9),the maximum rotation angle of vnis computed as δmax= 73.13◦with the minimum flyby radius(rflyby=1838 km). We noticed that the required rotation change of vncan not be completed via a single lunar gravity assist.Therefore,a lunar resonance orbit is employed as a bridge(or finding a proper p:q-resonance-circle and the LGA-p:q-arc).The p:q-resonance-circle is corresponding to a specific value of ρ,andtheguidelinetodetermineρ isthatboththeinitialand target vnare capable of hopping to a p:q-resonance-circle.
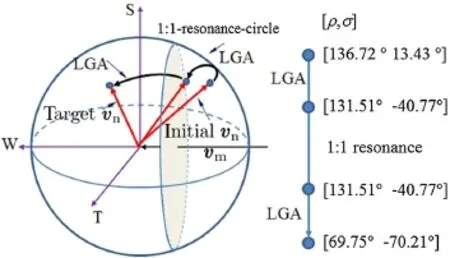
Fig.8 The change of[ρ,σ]for the escape from the Earth-Moon system
Based on δmax,ρ could be determined to be in 63.59◦-142.88◦and ρ=131.51◦is selected that is corresponding to a 1:1 lunar resonance orbit.Once ρ is determined,we performed a grid search of σ in terms of the concept of the LGA-p:q-arc,and σ=-40.77◦is finally chosen such that thelunarflybyradiusisnotquitelarge,whichimpliesthatthe gravity assist model in Fig.6 is a good approximation to the lunar close flyby in the restricted four-body dynamics.The lunar flyby radius is computed as follow in terms of Eq.(9)

The rotational change of vn(or changes of ρ and σ)is depicted in Fig.8.It is noted that the selection of ρ and σ for lunar resonance orbit is not unique,which implies that the utilization of lunar resonance orbits is quite flexible.
4.3 Capture with double lunar flybys
Let us now consider the connection of the 3rd and 4th segments.In terms of the orbital states at lunar flyby for the 3rd segment given in Table 5,the amplitude of vnis set to be 1.5885 km/s and the parameters[ρ,σ]of vnis[55.71◦,-117.43◦].If the minimum lunar flyby radius(= 1838 km)is adopted,the maximum rotation angle is computed as δmax=61.85◦.With an optimal rotation angle,the minimum orbital energy(see Eq.(10)is obtained to be-0.096 km2/s2,which theoretically results in a capture orbit in terms of the two-body dynamics but the reentry condition might not be satisfied.If the perigee of this capture orbit is deemed at the altitude of 200 km(for reentry),the orbital apogee reaches over 2 million km and the Sun’s gravitation can not be ignored.In this case,the two-body model is not accurate enough to approximate the trajectory in the restricted four-body dynamics.In the presence of the signifi-cant Sun’s gravitation,it is hard to use the method described in Sect.4.2 because there does not exist the lunar resonance orbitwithsmallratiossuchas1:1or1:2,etc.thatisusedtobe abridge.Weneedtoextendthetheconceptoflunarresonance orbits to accommodate the effect of the Sun’s gravitation.
In these circumstances,we implemented trajectory integration forward in time with a grid search of ρ and σ(the search domains are set to be 0≤ρ≤π,-π≤σ≤π,respectively).TheMoon’sdeparturetimeissettobethevalue given in Table 5.The trajectory integration is conducted in the restricted four-body dynamics,and the Moon’s gravitation is not counted if the spacecraft is close to the Moon(μm=0 in the Eq.(1)in the preceding and following 0.4 days(an empirical value)of lunar encounters).We focused ourattentiononthetrajectoriesthatwouldreturntothevicinity of the Moon.These trajectories are then re-optimized to construct the Moon-to-Moon transfers by exerting proper intermediate velocity impulses.It should be emphasized that the module of vnat Moon’s departure and return(not strictly constrained to be the values in Table 5)could be changed by adjusting intermediate velocity impulses.Among these Moon-to-Moon transfers,we found a solution in which ρ and σ of vnare[100.37◦,-164.64◦]at Moon’s departure and[99.71◦,-116.23◦]at Moon’s return,and the module of vnremains almost the same(intermediate velocity impulses are not necessary in this case).This Moon-to-Moon transfer takes about 12 months;and,therefore,it could be deemed an 1:12 lunar resonance orbit.An important reason to choose this solution is that the vnjust before the 4th lunar flyby is capable of resulting in atmospheric reentry condition via a single lunar flyby(vnchanges from[99.71◦,-116.23◦]to[90.53◦,173.51◦]with||vn||=1.5885 km/s).
In fact,the Moon-to-Moon transfer is employed to retargetthereentrycondition.Thechangeofρ andσ areshown in Fig.9.The dashed circular arc connects the two sets of ρ and σ via a Moon-to-Moon transfer in the restricted fourbody dynamics.This dashed arc vanishes in Fig.8 because the lunar resonance orbit is close to a two-body Keplerian orbit such that vnat Moon’s departure and return appear almost the same.The Moon-to-Moon transfer(a modified form of lunar resonance orbit considering the Sun’s gravitation)is deemed a bridge to connect the 3rd and 4th trajectory segments.It should be pointed out that,in order to further reduce the velocity impulses in the 3rd and 4th segments,the trajectory segment of“asteroid-Moon-Moon-reentry”is reoptimizedasawhole(seeSect.4.4fordetails)andonlyabout 103 m/s velocity impulses are required.The optimized solution does not show the lunar orbital resonance with integer ratio.
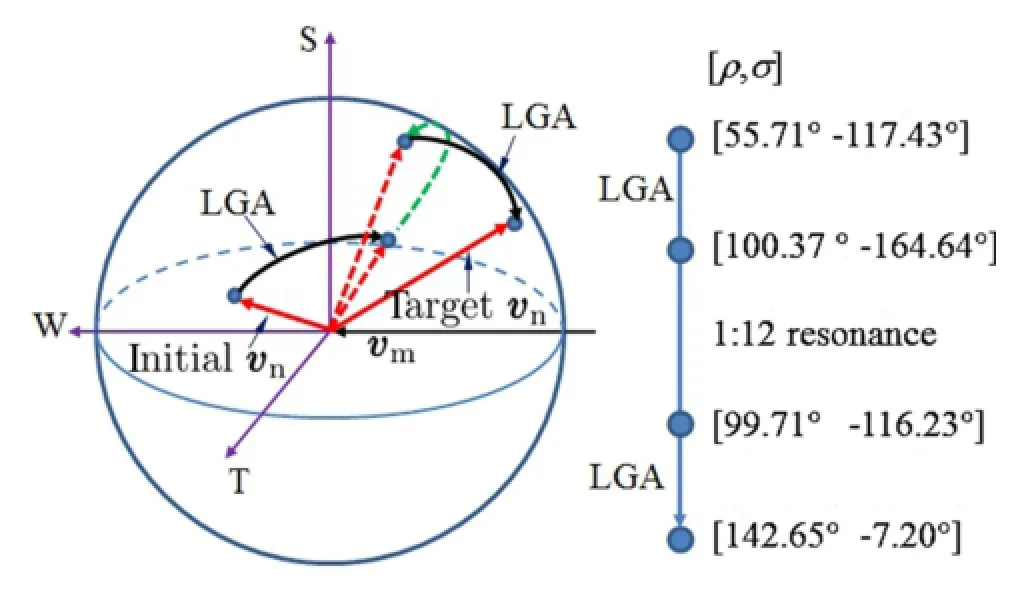
It is noted that the lunar resonance orbits depicted in Figs.8 and 9 appear in a different manner.In order to unify the concept of lunar resonance orbits in this study,we proposed two definitions:the two-body and multi-body lunar resonance orbit(or Moon-to-Moon transfer).In summary,if the flight trajectory is significantly influenced by multiple gravitational fields(see the case in Fig.9),it is termed the multi-body lunar resonance orbit with different initial and target vnthat are expressed by two distinct sets of the parameters[ρ,σ].It is noted that the amplitudes of the initial and target vnmight be also different.If the Earth’s gravity is dominant,it is termed the two-body lunar resonance orbit with almost the same initial and target vnthat corresponds to a set of the parameters[ρ,σ].Compared with the two-body lunar resonance orbit,the multi-body lunar resonance orbit in Fig.9 appears complex to some extent. From the point of view of flight mechanics,it could be also termed lunar-gravity-assisted 1:1 Earth resonance orbit.The multi-body lunar resonance orbit with necessary intermediate orbital corrections is a useful approach to change vnwith the consideration of the Sun’s gravitation,therefore serving asanenhancedbridgetoconnecttheinterplanetaryflightand the flight within the Earth-Moon system.
4.4 Resonance flyby orbits optimized in the restricted four-body dynamics
Based on the proposed methods described in Sect.4.2,the lunar relative velocity vectors(vn)just before and after lunar flybys are obtained,which are deemed the initial values of the solution to be obtained with subsequent optimization in the restricted four-body dynamics.For each lunar flyby,we proposed a model shown in Fig.10 for constructing lunar close flybys.First,we introduced a Moon-centered inertial frame xMyMzMthatisparallelto xEyEzE(seeFig.1),therelative velocity vectors before and after flyby are denoted by vinandvout),respectively,andthe angel between vinand voutis δ.It is noted that the transformation of orbital states expressed in the Moon-,Earth-and Sun-centered inertial frames is required,but not presented in detail herein.
At the lunar closest approach point,the spacecraft’s position and velocity vectors are denoted by rGAand vGA,respectively.They are approximately computed as follow in terms of rin,rout,and flyby radius rflyby
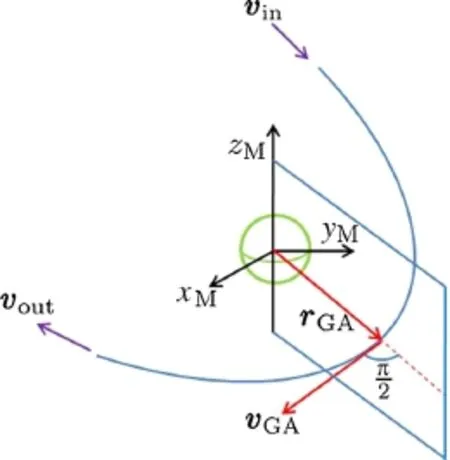
Fig.10 Modeling lunar gravity assist in the restricted four-body dynamics
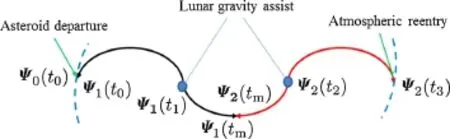
Fig.11 The capture trajectory in the restricted four-body dynamics
For the capture trajectory(from the asteroid departure to Earth reentry),the spacecraft orbital states are denoted by Ψ1(t1)at t1for the first lunar flyby and Ψ2(t2)at t2for the second lunar flyby.The orbital states of the asteroid at t0(asteroid departure time instant)are denoted by Ψ0(t0).The orbital states of the spacecraft at t0could be obtained by trajectory integration backward in time with Ψ1(t1)at t1,and Ψ1(tm)areobtainedbyintegrationforwardtotmthatisatime instant between t1and t2.In the same way,the orbital states Ψ2(tm)at tmare obtained by trajectory integration backward intimewithΨ2(t2)att2andtheorbitalstatesatEarthreentry(Ψ2(t3)att3)areobtainedbyintegrationforwardintime.The illustrationoftrajectoryintegrationisdepictedinFig.11.The velocity impulses are needed at t0and tmand some intermediate time instants to construct the whole capture trajectory. Finally,a nonlinear parameter optimization problem can be set up in Table 6,which is solved by NLP solver.
In the similar way,the escape trajectory(from an Earth elliptical orbit to asteroid rendezvous)is solved with additional constraints(the perigee of the eccentric orbit is between6578and6678kmandtheinclinationisbetween20◦and 90◦).Our experience shows that the design results using the concept of lunar resonance orbits provide good initial solutions that are then corrected in the restricted four-body dynamics.Finally,we obtained a whole impulsive trajectory starting from an Earth-centered elliptical orbit to the final Earth atmospheric reentry,including four times lunar flybys.

Table 6 The nonlinear optimization problem for the capture trajectory via two times lunar flybys
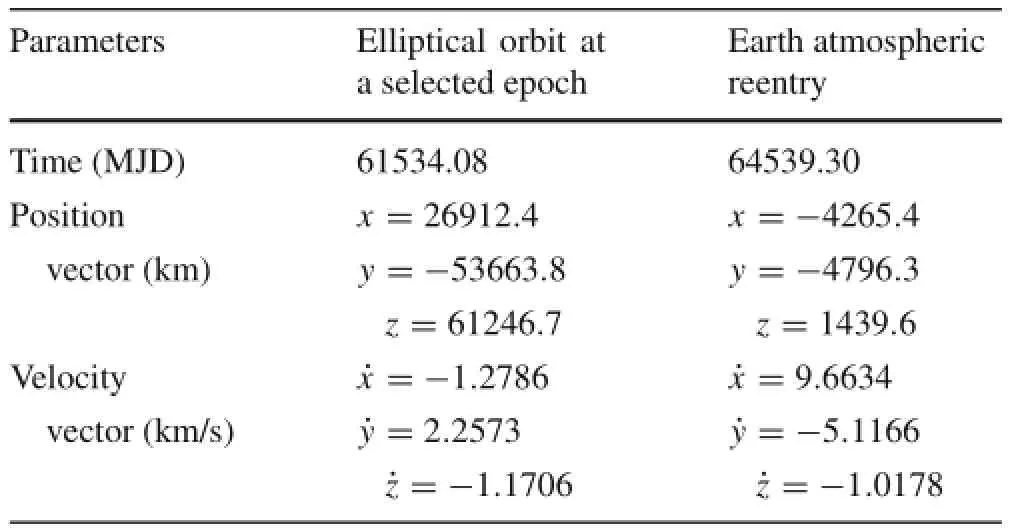
Table 7 The orbital states in the eccentric orbit and at Earth reentry(in the Earth-centered inertial coordinate frame)
Theorbitalstatesintheellipticalorbit(beforethe1stlunar flyby)ataselectedepochandtheorbitalstatesatatmospheric reentry are shown in Table 7.The epoch and orbital states in the first column in Table 7 is used to patch the low-thrust transfer from the low-Earth orbit,which is to be described in the next section.
5 Low-thrust orbital raising and escape from the Earth-Moon system
StartingfromacircularlowEarthorbitwith200kmaltitude,the spacecraft must endure a low-thrust multiple-revolution transfer to a highly elliptical orbit even with the thrust amplitude at its maximum value.The research on optimization of this type of multiple-revolution transfer is somewhat limited due to the difficulty of resolving the optimal bangbang thrusting structure.To tackle this trajectory segment,we defined two simplified and easily-understood steeringstrategies:perigee-centered tangential steering and apogeecentered inertial steering[14].As shown in Fig.12,the former is aligned with the orbital velocity direction,and the latter is perpendicular to the line connecting the osculating perigee and apogee.The tangential steering is employed for raising the altitude of apogee,and the inertial steering is utilizedformaintainingthealtitudeofperigeeabove200km.In this way,the circular orbit gradually becomes highly elliptical.The apogee of the transfer trajectory is continuously raised and the altitude of perigee does not change significantly.
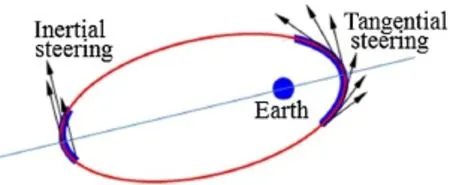
Fig.12 Illustration of the thrusting steering for multiple-revolution orbital raising
We then define θ to be true anomaly,and γ flight-path angle(theanglefromthelocalhorizontalplanetothevelocity vector)to model the proposed steering directions and the thrust vector.In this way,the pitch angle of the thrust vector(the angle from the local horizon plane to the thrust vector)is then computed as follows(see Ref.[14]for details)
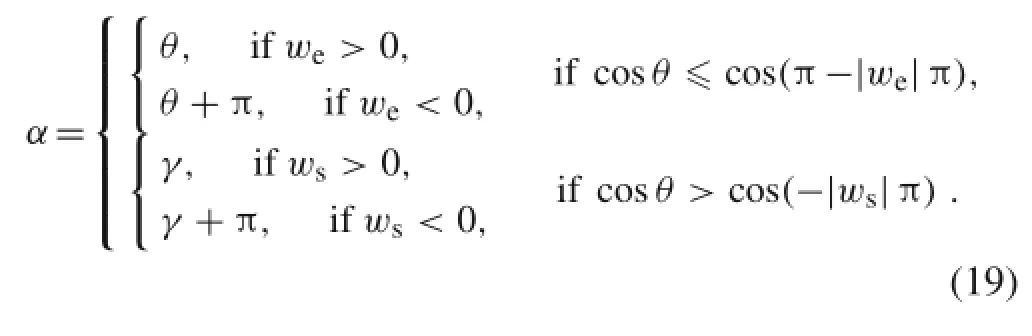
As a result,the projection of the thrust vector on the local horizon is denoted by Fr=F sinα and Fc=F cosα,a radial and a circumferential component.Meanwhile,we set the out-of-plane thrusting component to be null.These components can be trivially transformed into those expressed in the Earth-centered inertial coordinate frame.The parameters wsand weare set to be constant values(between-1 and 1).In fact,they can be variable with time and how to optimize wsand weis still challenging for the transfer from a low Earth orbit to a highly eccentric orbit.With empirical selection of wsand weby trial-and-error,we obtained a flightsequencewithalargenumberofthrustingandcoasting arcs,andthemulti-revolutiontransferisthencomputedusing numerical integration with the predefined guidance control laws in Eq.(19),considering the gravities of the Sun and the Moon.It is noted that if we=0 and ws/=0(no inertial steering is applied)when the orbit is eccentric,the perigee might decrease to below 200 km with the perigee-centered piecewise tangential steering only.For this case,the orbital raising is the main purpose and the perigee altitude maintenance is axillary,which results in the fact that|we|is much smaller than|ws|.
Finally,we=-0.0005 and ws=0.27 is selected and the low-thrust flight time is set to be 180 days.At the end of thelow-thrustorbitalraisingtrajectory,theosculatingorbital perigee and apogee are 8606 and 260654 km,respectively. Subsequently,the spacecraft needs to transfer to the elliptical orbit depicted in Table 7.By optimally selecting the orbital elements of the low Earth orbit and re-optimizing the orbital states at the selected epoch presented in Table 7,the low-thrust orbital raising trajectory is finally connected to the first lunar flyby by using a phasing orbit as a bridge. The apogee of this phasing orbit is beyond the lunar orbit,which is a necessary condition for lunar encounter.A relativelylongerthrustingarcnearperigeeisneededforboosting the spacecraft to this phasing orbit.
6 Converting velocity impulses into low thrust arcs
Alltrajectorysegmentsaredesignedusingvelocityimpulses as orbital maneuvers at the first step except for the one of orbital raising from a low Earth orbit to a highly eccentric orbit using low thrust only.After we obtained the designed solution with impulsive maneuvers,these velocity impulses are then converted into low thrust arcs accordingly.All exerted velocity impulses are classified into two cases.In thefirstcase,unpoweredcoastingarcsarelocatedbeforeand aftertheimpulseandinthesecondcasetheimpulseisexerted when the spacecraft just arrives at or departs from the asteroid.The illustration of these two cases is shown in Fig.13. For both cases,the starting time instant of the low thrust arcs to be converted is marked as t0(also the time instant for exertingtheimpulse)andthefinaltimeinstanttf.Forthefirst case,wespecifiedtwotimeinstantstA(orpointA)andtB(or point B)on each side of t0where tA=t0-c·Δtthrust,iand tB=tf+c·Δtthrust,i.Notethatcisanarbitrarypositivequantity and Δtthrust,i(tf=t0+Δtthrust,i)denotes the duration of thrusting arc that is converted from the i-th impulse.From A to B,the propulsion sequence is then defined as“coast-thrust-coast”.For the second cases(use asteroid departure as an example),the propulsion sequence is then defined as“thrust-coast”and tB=tf+c·Δtthrust,i.Based on the fundamentalrocketequation,thedurationofthrustingarcΔtthrust,iis estimated through the following equation

Fig.13 Illustration for converting impulses into low-thrust arcs

where mi0is the spacecraft mass before exerting the i-th impulsethatisdenotedbyΔvi,and F isthethrustamplitude.
According to the optimal control theory,the system Hamiltonian can be derived as follows
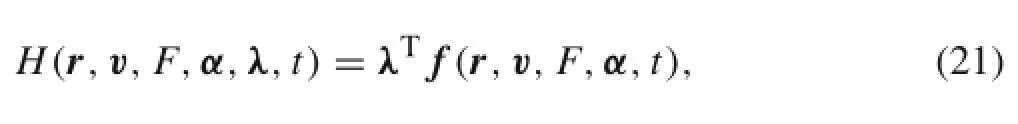
where f(r,v,F,α,t)is the right side of Eq.(1),and the differential equations of the costate variablescan be derived via computing the partial derivatives of the Hamiltonian with respect to the state variable s
The optimal thrusting direction considering the constraint|=1 is derived as

We then employed an indirect/direct hybrid optimization method[15]to solve the proposed optimal problem.Finally,the trajectory optimization problems are transformed into the nonlinear programming problems.The trajectories are numerically integrated in terms of the sequence of“coastthrust-coast”or“thrust-coast”(usingFig.13asanexample). With the orbital states at A(r∗(tA),v∗(tA))or at asteroid departure(rast(t0),vast(t0))that are obtained from the design solution with impulsive maneuvers,we can compute the states at B(r∗(tB),v∗(tB))that are constrained to the orbital states at tBin the designed solution.The time instants(tA,t0,tf,tB)are then constrained via setting a number of inequalities.These two cases of conversion are finally categorized to be the nonlinear programming problems listed in Table 8.The initial costate variables should be guessed. Because the low thrust arcs are relatively short,the iterations ofnonlinearprogrammingproblemsappeareasytoconverge.
7 Trajectory solution with the sample mass of 328 tons
The team from the Technology and Engineering Center for SpaceUtilization,ChineseAcademyofSciencesfinallysubmitted a solution with the design performance index of J=328313 kg,which is ranked first in this competition. The designed solution is presented in Table 9,and the flight trajectory is shown in Fig.14.It is noted that there are fourtimes at which lunar close flybys play important roles in carrying a hundreds-of-tons asteroid sample back to the Earth. Theflybyaltitudes(theflybyradiusminustheMoon’sradius)for these lunar flybys are no more than 1700 km,which indicates that the effect of lunar gravity assists is significant.The relative velocity(if it is denoted by v∞)in Table 9 is computed throughwhere rpand vpare the position and velocity at the lunar closest approach in a Moon-centered inertial coordinate frame.

Table 8 The nonlinear programming problem for converting velocity impulses into low thrust
Let us note the asteroid target“2003 SM84”.In fact,the semi-majoraxisoftheasteroid’sheliocentricorbitisslightly largerthan1astronomicunit(AU),suchthattheasteroidpossesses a roughly 6:7 resonance with the Earth,which means that the repeated heliocentric phase angles of the Earth and the asteroid is about 7 years.In this 7-year time interval,also the duration between the 2nd and 3rd lunar flybys,the asteroid orbits the Sun about 6 revolutions.
As shown in Fig.14,the trajectory segment of return(or the 3rd segment)is much longer than the outbound segment(or the 2nd segment),containing two segments of significant low thrust arcs(about 30 days and the equivalent impulse is about 100 km/s).The other thrusting arcs are much shorter and even harder to be identified in the figure.
The trajectory segment from a low Earth orbit to escaping fromtheEarth-MoonsystemisshowninFig.15.Thealtitude of apogee is raised by primarily using the tangential steering near perigee.The thrusting arcs near the apogee are quite short,which indicates the perigee altitude maintenance does not require much control effect.When the apogee altitude reaches about 260000 km,the spacecraft exerts a relatively longerthrustingmaneuvernearperigeetoboostitselfbeyond the lunar revolution orbit about the Earth.With about one orbitforphasingwithproperintermediateorbitalmaneuvers,the spacecraft encounters the Moon for the first time and is theninsertedintoa1:1lunarresonanceorbitviaasinglelunar flyby.After roughly a lunar orbital period about the Earth,the spacecraft encounters the Moon for the second time andthe close lunar flyby makes the spacecraft escape from the Earth-Moon system and then head for the asteroid.
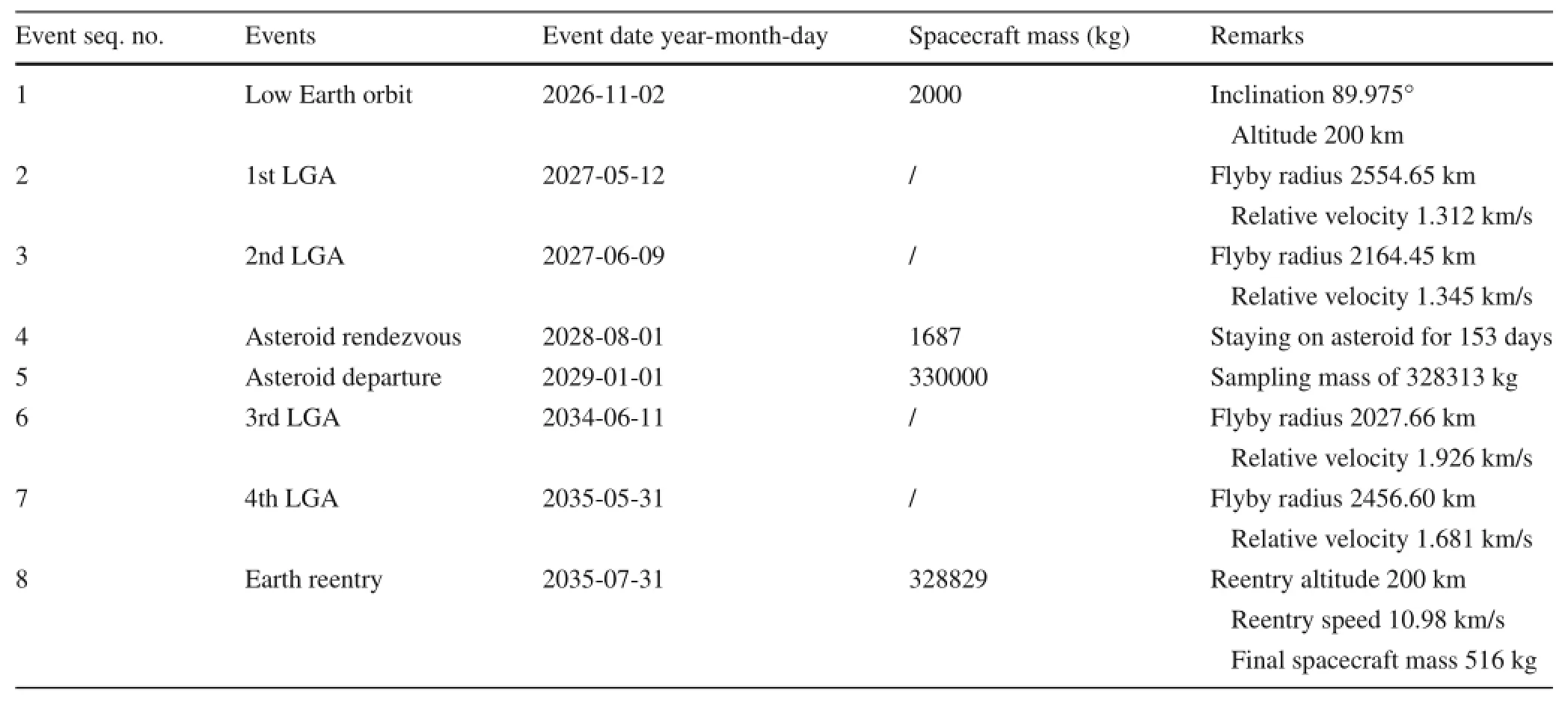
Table 9 A description of the designed solution

Fig.14 The optimally designed flight trajectory of sample-return mission in the Sun-Earth rotating coordinate frame

Fig.15 The trajectory segment to escape from the Earth-Moon system(including double lunar gravity assists)
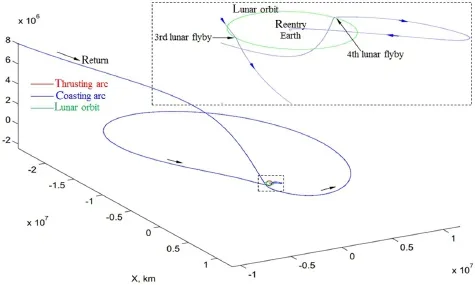
Fig.16 The return trajectory segment ended up with Earth atmospheric reentry(including double lunar gravity assists)
The trajectory from interplanetary space to Earth atmospheric reentry is shown in Fig.16.The equivalent velocity impulses for the segment shown in the figure are just a few meters per second;and,therefore the low-thrust arcsseemabsent.ForthecapturebytheEarth-Moonsystem,there are also two lunar gravity assists,which appear different from those for the escape(see Fig.15).If we consider that the spacecraft is in a resonance orbit with respect to the Moon,it is a roughly 1:12 lunar resonance orbit,in which the furthest distance from the Earth is about 20-million km that exceeds the Earth gravitational sphere.This lunar resonance orbit,interpreted to be multi-body resonance orbit,is an extension of the resonance orbit modeled in the two-body dynamics.After roughly a year,the spacecraft return to the Earth-Moon system again and Earth atmospheric reentry is achieved via the last lunar flyby.When we observe the heliocentric trajectory shown in Fig.17,the spacecraft is inserted into a heliocentric 1:1 resonance orbit with respect to the Earth.It is shown that the first(the third for the entire trajectory)lunar flyby occurs at the time instant when the range between the Earth and asteroid is almost smallest.The semimajor axis,eccentricity,and inclination of the spacecraft’s heliocentric orbit are much similar to those of the Earth after lunar flyby,but similar to those of the asteroid before lunar flyby.Asaresult,thereturnlegisatypicallow-energyflight,fullyexploitinglunargravityassistsviatheconceptoforbital resonance.The equivalent velocity impulses are about 103 m/s,muchlessthanthatoftheoutboundsegmenttotheasteroid.Thisresultisakeycharacteristicthatahundreds-of-tons of asteroid sample could be carried back.
8 Conclusions
We have reported our design methods for solving an NEA sample-return trajectory,which shows that returning a hundreds-of-tons asteroid or an asteroid sample is theoretically possible.The designed solution brings us a new understandingofspaceflightforNEA’sexplorationmissions. It is indicated that capturing a selected asteroid might not require much propellant and the asteroids,whose heliocentric orbits appear 6:7 or less resonance ratio with that of the Earth,are potential targets for asteroid(or asteroid sample)capture missions.Direct trajectory optimization with multiple-impulse maneuvers is proved to be effective to determine the target asteroid and required optimal velocity impulses.If the technology of solar electric propulsion is developed further,NEA’s sample return will become more and more promising.The designed solution,resolved just in a two-month time frame,can be deemed a baseline solution for future comparative study.
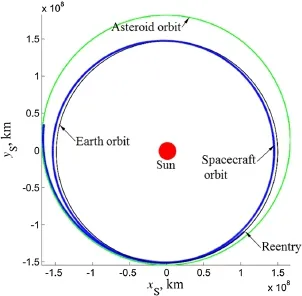
Fig.17 The heliocentric return trajectory segment(corresponding to the trajectory shown in Fig.15)
Meanwhile,we have realized that trajectory optimization in the Sun-Earth-Moon system might be quite challenging. In our design methods,orbital resonance and lunar grav-ity assists are deemed the crucial techniques to obtain the reported solution,and also proved to be efficient for designing flight trajectories for NEA exploration missions.The concept of lunar resonance orbits plays a role for fulfilling fuel-optimal escape from and capture by the Earth-Moon system.It is shown from this study that when the spacecraft flies by the Moon with the relative velocity up to 2 km/s(this is not the upper limit),it could be captured by the Earth-Moon system with quite few velocity impulses. Specifically,the lunar resonance orbit for achieving lowenergy atmospheric reentry is also deemed resonance with the Earth-Moon system with respect to the Sun.Moreover,the lunar resonance orbit model presented in this study provides an efficient design tool for constructing multiple lunar gravity assists.
We still think there might be other design methods for constructinglow-energytrajectories.Theinvariantmanifolds of halo orbits in the circular restricted three-body dynamics provide a good tool for trajectory design in multi-body dynamics.However,it is not explicitly employed for solving this problem.It is believed that the invariant manifolds and lunar resonance orbits could be combined for designing a variety of low-energy transfer trajectories in the Sun-Earth-Moonsystem,especiallyforthetrajectoriesforcapturingthe asteroid sample into lunar orbit,which is the scenario of the asteroid redirect mission.
AcknowledgmentsWewouldliketoexpressourgratitudetotheChinese Society of Theoretical and Applied Mechanics and the State key LaboratoryofAstronauticDynamicsforreleasingthisinterestingproblem,whichgaveusachancetoconductresearchonthetrajectorydesign for NEA exploration missions.Meanwhile,this work was also supported by the National Natural Science Foundation of China(Grant 11372311)and the grant from the State key Laboratory of Astronautic Dynamics(2014-ADL-DW0201).In addition,we can provide the datafilesandverificationprogramsforoursubmittedsolution,andanyone who is interested in this solution can send a request via Email to gaoyang@csu.ac.cn.
Appendix:Ephemerides of the Sun,the Moon,and the asteroid“2003 SM84”
See Tables 10,11,12.

Table 10 The epoch and classical orbital elements of the Earth(referenced in the heliocentric ecliptic coordinate frame)

Table 11 The epoch and classical orbital elements of the Moon(referenced in the Earth-centered ecliptic coordinate frame)

Table12 Theepochandclassicalorbitalelementsoftheasteroid“2003 SM84”(referenced in the heliocentric ecliptic coordinate frame)
References
1.The global trajectory optimization competition portal,http:// sophia.estec.esa.int/gtoc_portal/,cited on December 12(2014)
2.Elvis,M.:Let’s mine asteroids for science and profit.Nature 485,549(2012)
3.Brophy,J.,Friedman,L.,Culick,F.,et al.:Asteroid retrieval feasibility study.Keck Institute for Space Studies,California Institute of Technology,Jet Propulsion Laboratory(2012)
4.GarcíaYárnoz,D.,Sanchez,J.P.,McInnes,C.R.:Easilyretrievable objects among the NEO population.Celest.Mech.Dyn.Astron. 116,367-388(2013)
5.Lladó,N.,Ren,Y.,Masdemont,J.,et al.:Capturing small asteroids into a Sun-Earth Lagrangian point.Acta Astron.95,176-188(2014)
6.Baoyin,H.,Chen,Y.,Li,J.:Capturing near Earth objects.Res. Astron.Astrophys.10,587-598(2010)
7.Hasnain,Z.,Lamb,C.A.,Ross,S.:Capturing near-Earth asteroids around Earth.Acta Astron.81,523-531(2012)
8.Urrutxua,H.,Scheeres,D.,Bombardelli,C.,et al.:What does it taketocaptureanasteroid?Acasestudyoncapturingasteroid2006 RH120,24th AAS/AIAA Space Flight Mechanics Meeting,Paper 2014-276.San Diego,CA,United states(2014)
9.Ross,S.,Scheeres,D.:Multiplegravityassists,capture,andescape in the restricted three-body problem.SIAM J.Appl.Dyn.Syst.6,576-596(2007)
10.Schoenmaekers,J.,Pulido,J.,Cano,L.:SMART-1 Moon mission:trajectory design using the Moon gravity,Technical Report SI-ESC-RP-5501,ESA,European Space Operation Center,Darmstadt,Germany(1999)
11.Campagnola,S.,Russell,R.:The endgame problem part 2:Multibody technique and T-P graph.J.Guid.Control Dyn.33,476-486(2010)
12.Cuartielles,J.,Alessi,E.M.,GarciaY.,etal.:Earthresonantgravity assists for asteroid retrieval missions.International Astronautical Congress,Beijing,China,IAC-13-C1.7.8(2013)
13.Alessi,E.,Colombo,C.,Sanchez,J.,et al.:Out-of-plane extension of resonant encounters for escapeand capture,International Astronautical Congress,Beijing,Republic of China,IAC-13-C1.9.1(2013)
14.Gao,Y.:Near-optimal very low-thrust Earth-orbit transfers and guidance schemes.J.Guid.Control Dyn.30,529-539(2007)
15.Gao,Y.,Kluever,C.:Low-thrustinterplanetaryorbittransfersusing hybrid trajectory optimization method with multiple shooting,Paper 2004-5088,AIAA/AAS Astrodynamics Specialist Conference,August 16-19,2004,Providence,RI,United states(2004)
17 April 2015/Revised:5 September 2015/Accepted:15 September 2015/Published online:29 October 2015
✉ Yang Gao gaoyang@csu.ac.cn
1Key Laboratory of Space Utilization,Technology and Engineering Center for Space Utilization,Chinese Academy of Sciences,Beijing 100094,China
2University of Chinese Academy of Sciences,Beijing 100049,China
3Academy of Opto-Electronics,Chinese Academy of Sciences,Beijing 100094,China
- Acta Mechanica Sinica的其它文章
- Delayed detached eddy simulations of fighter aircraft at high angle of attack
- Plate/shell topological optimization subjected to linear buckling constraints by adopting composite exponential filtering function
- Numerical simulations of the process of multiple shock-flame interactions
- Analytical and finite-element study of optimal strain distribution in various beam shapes for energy harvesting applications
- The comparative analysis of rocks’resistance to forward-slanting disc cutters and traditionally installed disc cutters
- Modal parameter identification of flexible spacecraft using the covariance-driven stochastic subspace identification(SSI-COV)method

