Vibration analysis of hard-coated composite beam considering the strain dependent characteristic of coating material

W.Sun·Y.Liu



RESEARCH PAPER

Vibration analysis of hard-coated composite beam considering the strain dependent characteristic of coating material

W.Sun1·Y.Liu2

©The Chinese Society of Theoretical and Applied Mechanics；Institute of Mechanics，Chinese Academy of Sciences and Springer-Verlag Berlin Heidelberg 2016

The strain dependent characteristics of hard coatings make the vibration analysis of hard-coated composite structure become a challenging task.In this study，the modeling and the analysis method of a hard-coated composite beam was developed considering the strain dependent characteristicsofcoatingmaterial.Firstly，basedonanalyzingthe properties of hard-coating material，a high order polynomial was adopted to characterize the strain dependent characteristics of coating materials.Then，the analytical model of a hard-coated composite beam was created by the energy method.Next，usingthenumericalmethodtosolvethevibrationresponseandtheresonancefrequenciesofthecomposite beam，a specific calculation flow was also proposed.Finally，acantileverbeamcoatedwithMgO+Al2O3hardcoatingwas chosenasthestudycase；underdifferentexcitationlevels，the resonance region responses and the resonance frequencies of the composite beam were calculated using the proposed method.The calculation results were compared with the experiment and the linear calculation，and the correctness of the created model was verified.The study shows that compared with the general linear calculation，the proposed method can still maintain an acceptable precision when the excitation level is larger.

Hard coating·Composite beam·Vibration analysis·Strain dependent characteristics

1 Introduction

The hard coating is a kind of coating material prepared by metals，ceramics or their mixtures.Usually，the hard coating is used as the thermal barrier coating，anti-friction，and anti-erosion coating.In recent studies［1-3］，it was found that the hard coating also possessed good damping qualities.Now，a new research field about damping vibration by hard coating has received a reasonable amount of attention［4-6］.Compared with traditional surface treatments，suchastheviscoelasticdampers，thebiggesttechnical advantage is that the hard coating can maintain consistent damping characteristics at high temperatures or the high corrosion environment［7］.So this vibration reduction technologycanbeadoptedforallkindsofpowerequipment，such as the turbine engine.

To effectively implement the hard-coating damping technology，a reliable analysis model needed to be created to support the hard-coating damping design.However，some researches［8-10］have shown that the mechanical parameters of hard coating changes with the response amplitude of structure，and this phenomenon was named as the strain dependent characteristic.The strain dependent characteristic of hard coating makes the establishment of an analysis model of hard-coated composite structure become very difficult.Due to the strain dependent characteristics of hard coatings，the coated structure usually exhibits nonlinear behavior.For example，both Ivancic and Palazotto［11］and Blackwell et al.［12］tested the titanium plate coated MgO+Al2O3hard coating and found the forced frequency response of composite plates was not symmetric about the resonance frequency，and the resonance frequency decreased with the increase of excitation level，indicating stiffness non-linearity.The strain dependent characteristicof hard coating is a unique material nonlinear behavior，and how to deal with this nonlinear becomes a challenging task.

Now，some scholars have developed some analysis models about hard coating and most of these models belong to micro material models.For example，Tassini et al.［13］studied the microscopic structure of hard coating material and presented a phenomenological model that characterizes non-linear mesoscopic elastic behaviors.This model can reproduce the basic features of the observed damping behaviorofzirconiacoatings.Torvik［14］developedaslipdamping modeltocharacterizetheidealizedmicrostructurecharacteristic of hard coating and analyzed the energy dissipation in a lap joint of composite structure.Abu Al-Rub and Palazotto［15］created the representative volume element model of hard coating to assess the main micromechanical mechanisms responsible for the experimentally observed nonlinear damping phenomena.The abovementioned research results show that the internal friction in the hard coating creates energy dissipation，and these researches make a significant contribution for understanding the nonlinear dynamics mechanismandvibrationreductionmechanismofhardcoatings.

However，it is not realistic to entirely depend on these micromaterialmodels.Forthehardcoatingdampingdesign，the macro dynamics models of hard-coated composite structures need to be created.But，unfortunately，the current researchwasinadequateforthisstudyfield.Therefore，Green et al.［16］proposed a less elegant form of the Iwan model to describe the response of a coated beam.In addition，Reed［17］did a similar research and used the nonlinear adjusted Iwan model to analyze the free response and the forced response of a hard coated beam and reproduced the nonlinear vibration phenomenon observed in experimental study. In their researches，the Iwan model is a single degree of freedom model and also can be thought of as a kind of phenomenological model，which is used to characterize the experimental phenomenon.The model does not include the geometry and the material characteristics of hard coating，so it cannot effectively guide hard-coating damping design. Therefore，a hard coating damping design is urgently needed that creates the dynamics analysis model，which can consider both the material and the geometric parameters of composite structure，with a typical model，such as finite element model and an analytical model.Recently，the finite element modeling of hard-coated composite structure has been studied.For example，in the research of Filippi et al.［18］，thehardcoatingparameterswithstraindependentcharacteristics were simplified as a linear expression；the finite element modeling technology was adopted to analyze the vibration characteristics of compressor blade coated hard coating.Also，Li et al.［19］did a similar study；the hard coating parameters were expressed by a cubic polynomial introduced into the finite element model to solve the resonance frequency and the vibration response of a hard-coated cantilever plate.But，to the authors’knowledge，the analyticalmodelingofhardcoatingcompositestructureconsidering the strain dependent characteristic has not been sufficiently studied.

To create the dynamics model of hard-coated composite structure，the mechanical parameters with a strain dependent characteristic should be obtained in advance.Fortunately，this research has made good progress.For example，Patsias et al.［20］tested the response decays of a Nimonic C-263 beam specimen coated with a hard coating under different excitation levels and extracted the damping and the modulus of elasticity of the coating corresponding to different strains.In addition，Torvik［8］carefully measured the specimen dimensions，weights，natural frequencies，and system loss factors before and after coating and developed an identification method to obtain the storage modulus and loss modulus corresponding to different strain levels. Then，Reed et al.［9］set up a novel vibration experiment system and proposed the specific test methods to get the strain dependent stiffness and the damping properties of hard coatings at high strain levels.Also，Tassini et al.［10］presented an experimental-numerical procedure to identify the mechanical parameters with strain dependent characteristics and analyzed the difference of mechanical parameters of hard coating prepared by air plasma spraying（APS）and electron beam-physical vapour deposition（EB-PVD）.These researches provide an important support for dynamic modeling of hard-coated composite structure.

Thefocusofthisstudyisonthedevelopmentofananalytical model of a hard-coated composite beam considering the strain dependent characteristic of the coating material.This paper is organized as follows.In Sect.2，based on analyzing the properties of hard-coating materials，the high order polynomial was adopted to characterize the strain dependent characteristic of coating materials.In Sect.3，the analytical model of a hard-coated composite beam was created by the energy method.In Sect.4，using the numerical method to solve the vibration response and the resonance frequencies ofcompositebeam，aspecificcalculationflowwasproposed. In Sect.5，a cantilever beam coated with MgO+Al2O3hard coatingwaschosenasastudycase，and，underdifferentexcitationlevels，theresonanceregionresponseandtheresonance frequencies of composite beam were calculated using the proposed analytical model and the calculation procedures. The calculation results were compared with the experiment and the linear calculation，and the correctness of the createdmodelwasverified.Finally，someimportantconclusions about this study are listed in Sect.6.

2 Characterizing the mechanical parameters of hard coating by the high order polynomial

The mechanical parameters of hard coating have unique mechanical characteristics，which can be summarized as the following three aspects:（1）the damping of hard coating is effective over a greater temperature range and the damping ability failure does not occur at a higher temperature environment like the viscoelastic material；（2）the hard coating materials have better damping properties than common metals，but do not provide the same level of damping that viscoelastic materials do，so the loss factors of both coating and substrate should be considered during the practice of hard-coated composite structure modeling；（3）the hard coating materials have nonlinear characteristics and its elasticity modulus will change with the response amplitude of composite structure，which is called the strain dependent characteristic.

Here，the strain dependent characteristic is mainly considered.The elastic modulus of hard coating is expressed as complexmodulus ，andthefollowingformulacanbeused to describe the strain dependent characteristic，

where*refers to a complex value，the subscript c refers to“coating”and the subscript R and I refer to“real part”and“imaginary part”of the complex modulus.EcR（εe）and EcI（εe）are also named as the storage modulus and the loss modulus，andbothofthemareafunctionofequivalent strain εe.

For convenience，the complex modulus of hard coating can be expressed by polynomial［18］，then the storage and the loss modulus in Eq.（1）are shown as

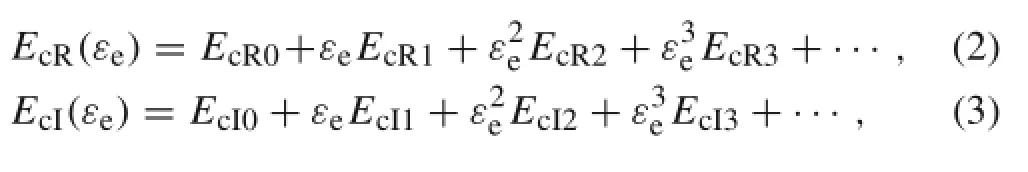
where EcR0and EcI0are the storage and the loss modulus without considering the strain dependent characteristic of hard coating，EcRi，EcIi（i=1，2，3，...）are the specific coefficients of strain dependent storage modulus and loss modulus，and i is the order of the polynomial.Furthermore，the complex modulus of hard coating can be also expressed as

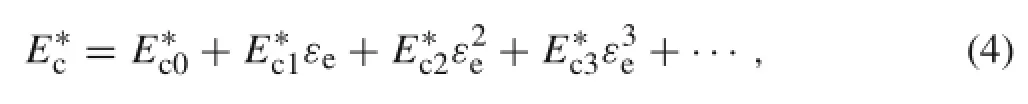
where

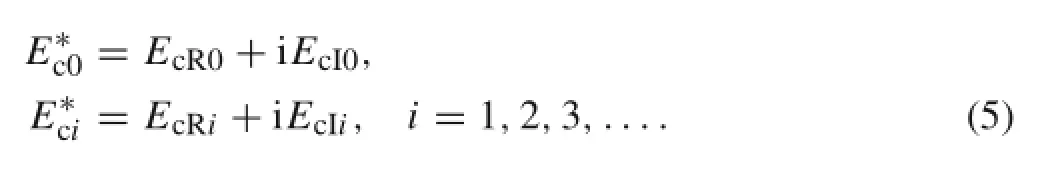
Fig.1 Mechanical parameters of MgO+Al2O3with strain-dependent characteristics.a Storage modulus.b Loss modulus

Themechanicalparametersofhardcoatingobtainedfrom testingareusuallythediscretepointvalues，thatis，eachmodulusvalueiscorrespondingtoaspecifiedstrainamplitude.To characterize the mechanical parameters of hard coating with thestraindependentcharacteristic，thesediscretepointvalues need to be fitted by a polynomial.In Fig.1，the mechanical parameters of MgO+Al2O3are expressed by the red asterisk，which were obtained by experiment in Ref.［9］.It can be seen that these discrete point values cannot be fitted by a linearfunctionandhavetobefittedbyahighorderpolynomial. Here，a cubic polynomial was chosen and the fitting curve is also shown in Fig.1.

The expressions of the cubic polynomial are

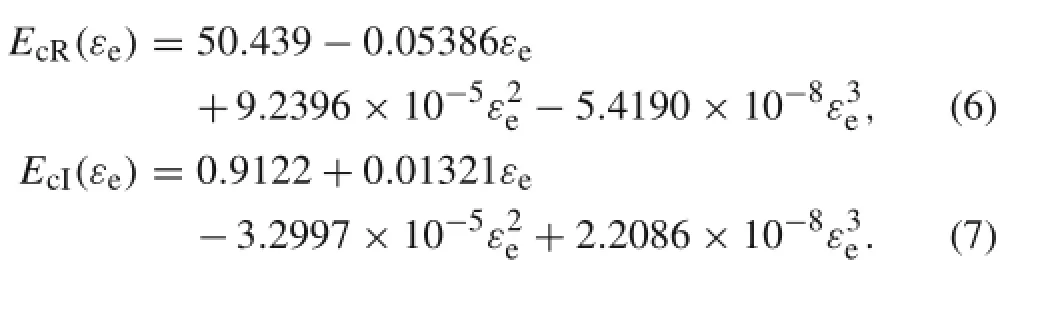
3 Analytical modeling of hard-coated composite beam

Inthissection，theanalyticalmodelingofahard-coatedcompositebeamwasstudiedunderbaseexcitation.Theschematic diagramofthehard-coatedcompositebeamunderbaseexcitation is shown in Fig.2a.The x axis is set to locate at the neutral axis of the composite beam，the length and width of beam are L and b respectively，and the mass of unit length is m.The deflection curve of the beam at movement condition is set as w（x，t）and the expression of base excitation

is ug（t）=，where UGis the level of base excitation and ω is the angular frequency of excitation.Figure 2b shows a small part of the beam section.Here，Hc，Hsrepresents the thickness of the hard coating and metal substrate respectively，andδ isthedistancebetweentheinterfaceofthe coating-substrate and the neutral axis.Then，the distance of the coating surface and the x-axis is Hc+δ，and the distance of metal substrate and x-axis is Hs-δ.

Both the elastic modulus of hard coating and the metal substrate need to be expressed as a complex modulus.The expression of hard coating materials is shown in Eq.（1）and the modulus of metal substrate is expressed as

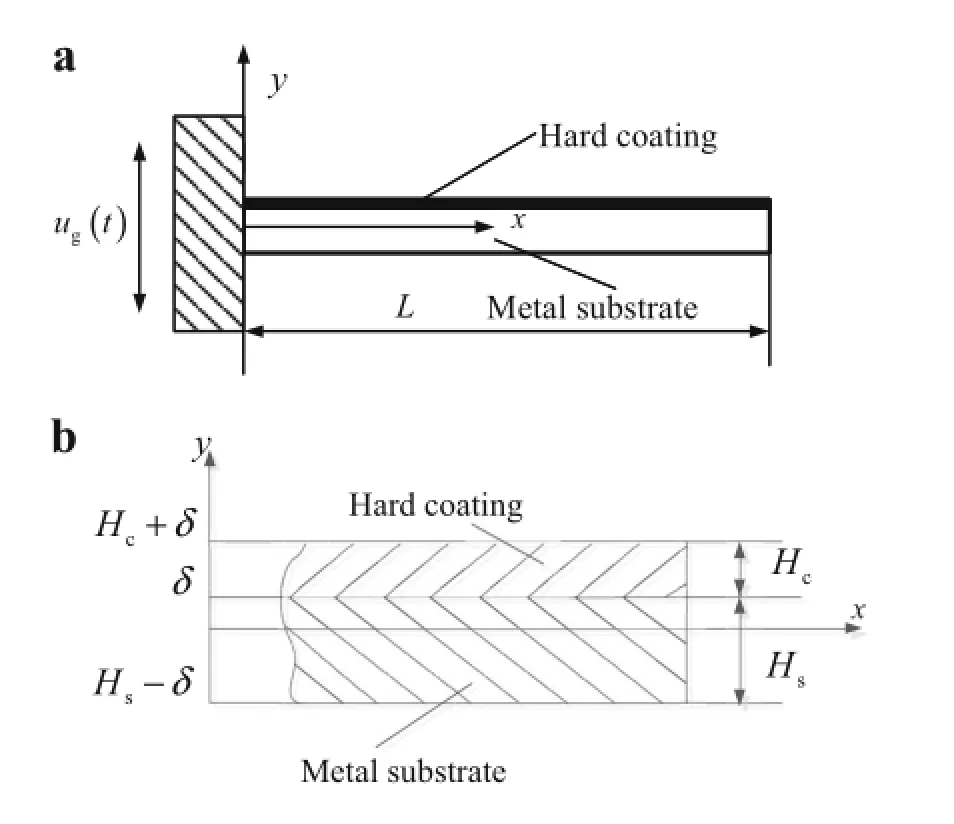
where the subscript s refers to“substrate”，EsR，EsIare the storagemodulusandlossmodulusofthemetalsubstrate，and both of them are set as a constant in this study.

For simplification，the rotation of the beam cross section is ignored.Then，the movement of each point on the beam can be described by the transverse displacement d（x，t）of the neutral axis and the expression is

Thestrainε（x，t）ofeachpointonthebeamcanbeexpressed as

where z isthedistancebetweenthepointonthecrosssection and the neutral axis.

Because the complex parameters or model are considered intheanalyticalmodel，thestrainε（x，t）isalsocomplex.But， for convenience，only material parameters are expressed by the complex symbol in the whole study.The strain ε（x，t）can be used to solve the maximum value of strain and the equivalent strain εecan be expressed as

where Re（·）and Im（·）refer to the function of extracting the real and imaginary part.It can be found from the Eq.（11），the equivalent strain εeis independent with time.

According to Oberst beam theory［21］，the distance δ between the interface of coating-substrate and the neutral axis can be calculated.But，due to the nonlinear characteristics of the hard-coating elasticity modulus，the distance δ is notaconstantanymoreandisacomplexexpressionabout x. Considering the change of δ is very small，it is assumed that the distance δ is still a constant and the solution formula is

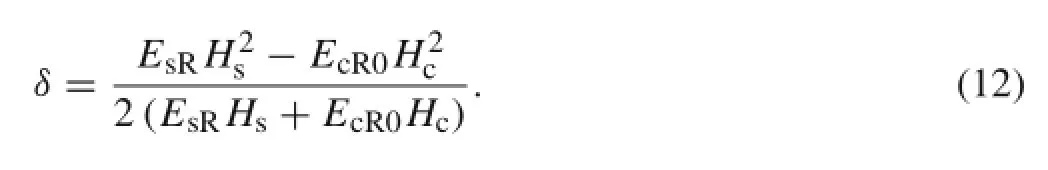
Considering the strain dependent characteristic of hard coating，the expression of strain energy of the composite beam is

Here，

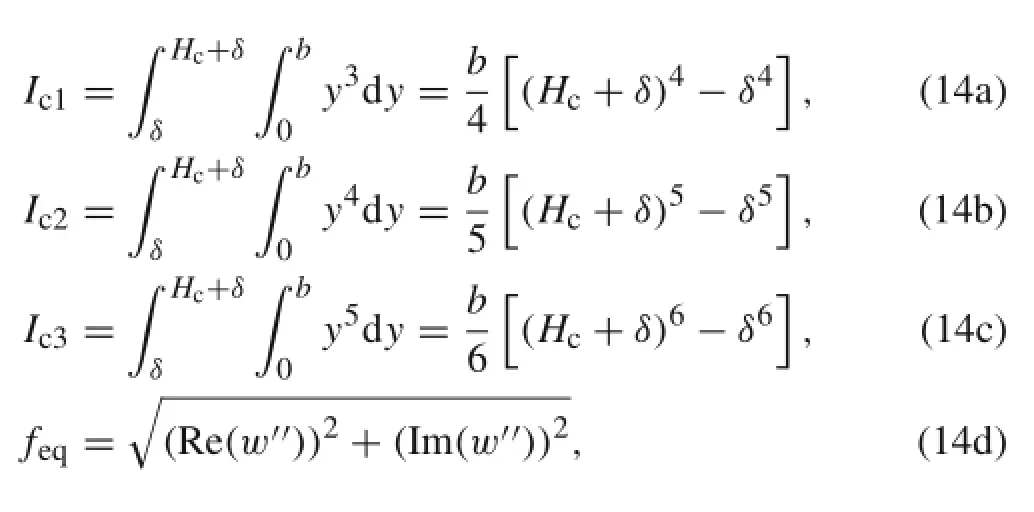
wherethemeaningofvariable Ij（j=s，c0，c1，c2，c3）isthe moment of inertia of the beam section and the operator symbol（）′referstoderivatex.Itcanbeseen，forthehard-coating material，only a 3rd order polynomial is adopted in Eq.（13），which is corresponding to the Eqs.（6）and（7）.In addition，it should be noted that the expression of strain energy contains the material damping of both hard coating and substrate.

Thekineticenergyofthecompositebeamcanbeexpressed as

where m=ρsHs+ρcHc，ρsand ρcare the density of the substrate and hard coating material，respectively，and the operator symbol（•）refers to derivate t.

In addition to material damping of the hard coating and substrate，the boundary conditions damping and fluid damping in air also should be contained in the composite structure system，and this damping can be equivalent to viscous damping，which are called the remaining equivalent viscous damping in this study.The remaining equivalent viscous damping can also dissipate the energy of the composite system and the expression is shown as follows

wherec isthecoefficientoftheremainingequivalentviscous damping.

Here，theGalerkindiscretemethodwasadoptedtoreduce the order of this nonlinear problem，and it was assumed that the deflection curve expression of the composite beam was

where φj（x）is the j-order modal shape，which can be thought consistent with the modal shape of uncoated beam，χj（t）is the j-order modal participation factor，and N refers to the number of considered modes.

Substituting Eq.（17）into Eqs.（13），（15）and（16）can yield

where

Then，the Lagrange equation can be listed as follows

If only the j-order frequency vibration is considered，it can be assumed

Substituting the Eqs.（18）and（21）into Eq.（20）can yield

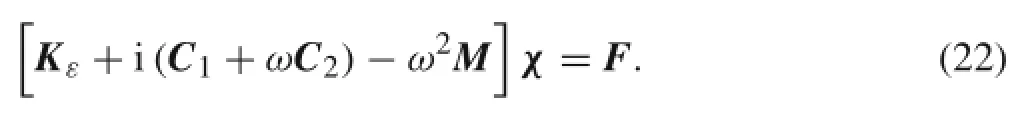
Inthisequation，Kεisanonlinearstiffnessmatrixconsidering the strain dependent characteristic of hard-coating materials，C1refers to the material damping matrix，C2refers to the remainingequivalentviscousdampingmatrix，M isthemass matrix，χ can be thought as a response vector independent with time，and F is the excitation vector.

The matrixes Kε，C1，C2，M are all a N-order square matrix and the vectors χ and F are a N-order vector.Among them，the element of the l-th row and j-th column of nonlinear stiffness matrix Kεis

The material damping matrix C1and the nonlinear stiffness matrix Kεcan be assembled into a complex stiffness matrix ，and the element of the l-th row and j-th column is

The element of the l-th row and j-th column of mass matrix M is

The element of thel-th row and j-th column of remaining equivalent viscous damping matrix C2is

For convenience，the j-th order remaining equivalent viscous damping coefficient cjcan be simplified as

where ωjis the j-th order natural frequency and ζjis the j-th order modal damping ratio obtained by testing.Here，it is assumed that the boundary damping and air damping do not change after coating，then the modal damping ratio ζjcan be introduced according to the damping of the uncoated beam.

If ignoring the non-diagonal elements，the matrix C2becomes an N-order diagonal matrix，the element of the l-th row and l-th column is

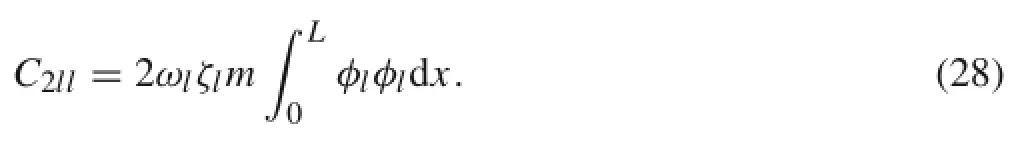
The element of the excitation vector F can be described as

Then，the dynamics model of the composite beam，considering the strain dependent characteristic of hard coating，is created.In this model，both the material damping and the remainingequivalentviscousdampingareconsidered.Based on this model，the resonance frequencies of the composite beam with the change of excitation levels and the nonlinear vibration response can be solved.

4 Solution of vibration response and resonance frequency of composite beam

4.1 Solution of vibration response

Duetothestraindependentcharacteristicofthehard-coating material，Eq.（22）becomes a nonlinear algebraic equation. The Newton-Raphson method was adopted to solve the vibrationresponseofthecompositebeam.Equation（22）can be transformed as

Because the residual value vector r contains the Re（χj）and Im（χj）items，also，eachelementofvectorχ canbeexpressed as Re（χj）+iIm（χj），so the Jacobi matrix˜J of vector r can be described as

where∂r/∂χR=r′Ris a N-order square matrix，and the element of l-th row and p-th column is

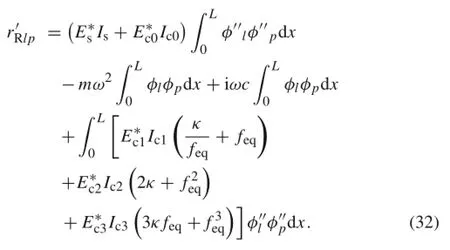
Here，

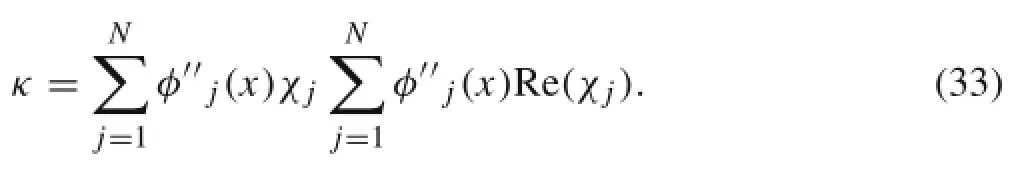
In the same way，the element of the l-th row and the p-thcolumn of matrix

Here，

Extract the real and the imaginary part of the vector r and χ respectively，and form two new vectors，which are shown as follows

Then，theiterativeformulasoftheNewton-Raphson method for the Eq.（30）can be gotten

where n is the iteration number.

Fig. 3 The procedure of solving the vibration response of the hardcoated composite beam

Using the iterative calculation of Eq.（37），the solution with certain precision can be obtained，and the precision of the solution can be controlled by setting the maximum norm value of vectorWhen attaining termination conditions，the vectorshould be transformed into the complex solution χ，and then the deflection and strain of the beam can be solved by Eqs.（17）and（10）.Finally，the vibration response of the compositebeamunderbaseexcitationisobtainedbyEq.（9）. The whole solution procedure is shown in Fig.3 and some steps are explained as follows.

For step 1，it is necessary to determine the iterative initial value，which can be obtained according to the following equations

where the stiffness matrix K does not contain the strain dependent characteristic of hard-coating material，that is，the mechanical parameter of hard coating is introduced into the model according toThe element of the l-th row and the j-th column of stiffness matrix K is

For step 7，the convergence condition is defined as the norm 2 of vector r less than the set value，that is，

TOL.

Fig.4 The procedure of solving resonance frequency of the hardcoated composite beam

In the last step，the output values，such as the deflection，strain and displacement response of the composite beam are obtained by calculating the modules of the relevant complex solution.

4.2 Solution of resonance frequency

When calculating the resonance frequency of the composite beam，theresonanceresponseshouldbeobtainedinadvance，so the calculation method of vibration response is described firstly at the above section.

Neglecting the damping and the excitation force items in Eq.（22），the characteristic equation considering the strain dependent characteristic of hard-coating materials can be expressed as

Here，the iterative method was also adopted to solve the resonance frequency of the composite beam.The calculating procedure is shown in Fig.4.

For step 1，to obtain the initial valueof resonance frequency，the strain dependent characteristic of hard-coating material is neglected，the solution expression is

For step 2，corresponding to the initialvalue，the calculation equation of resonance response is

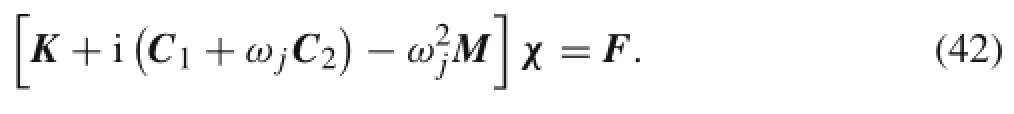
Table 1 The geometric parameters of the composite beam

Similar with the response calculation，in step 6，the convergence condition is defined as the norm 2 of the difference between two adjacent frequencies；the expression is

5 Study case

5.1 Vibration experiment of hard-coated composite beam

TheTi-6Al-4Vcantileverbeamwaschosenasastudyobject and one side of the beam was coated with the MgO+Al2O3hard coating.The method of preparing the hard coating was APS and the proportion of coating materials and depositing technology were similar with Refs.［9］and［12］.The geometric parameters of substrate and hard coating are listed in Table 1 and the densities of substrate and the hard coating are4420and2565kg/m3，respectively.Thematerialparameters of hard coating have the strain dependent characteristic，which are considered according to Eqs.（6）and（7）.

TheexperimentalsystemisshowninFig.5.Inthesystem，the electromagnetic vibration shaker is the base excitation equipment and the Doppler laser vibrometer is the vibration picking equipment.The vibration picking point is located at the lower part of the composite beam and the distance between the point and the root of beam is 22.5mm.Table 2 lists the detailed instruments used in this test.It should be notedthatanaccelerometerwasplacedinthefixtureandthis sensor was used to monitor the base excitation amplitude of the fixture.Another accelerometer was used to control the amplitude of the vibration shaker.It has been found that the measurement values are different between the two accelerometers.In this study，the measurement value in the fixturewaschosenasthebaseexcitationamplitude.Toensure theconsistentboundaryconditionsbetweentheuncoatedand coated beam，a torque wrench was chosen and the tightening torque of the bolt was 34Nm in the fixture.

Fig.5 Experimental system for the hard coated cantilever beam

Table 2 The instruments used in this test

Herein，for the composite beam，the calculation of the 3rd order resonance frequency and the vibration response near the resonance region were chosen to display the feasibility of the proposed method.According to the needs of analytical calculation and verifying the analytical calculation results，the first 6-order modal damping ratios of the uncoated beam，the natural frequencies of the composite beam，and the 3rd order resonance frequency and the resonance region response under different excitation levels（0.1，0.3，0.5，0.7，0.9g）were tested.Among them，the modal damping ratios of the uncoated beam were obtained by the half power bandwidth method from the sweeping response of the composite beam under 0.1g.The natural frequencies of the composite beam were obtained from the three dimensional（3-D）waterfall figure of sweeping response under 0.1g.In this study，the 0.1g excitation level was thought to be very low，which cannot lead to the occurrence of strain dependent characteristics of hard coating，so the natural frequencies obtained by experiment are thought of as the linear natural frequencies.The 3rd order resonancefrequencyandtheresonanceregionresponsewerealso acquired by this 3-D waterfall figure of sweeping response，and the sweeping direction was from high frequency to low frequency.All the tested results are listed in Tables 3，4，and 5.It should be noted that all experiments were done three times.Because the vibration shaker is a stable excitation equipment，so the three measured results were almost the same.Then only one set of data was used in this study.

It can be seen from Table 5，the 3rd order resonance frequency of the composite beam decreases with the increase of excitation level.The sweeping response in the considered frequency range is shown in Fig.6.It should be explained that the labels of excitation levels in Fig.6 are the settingamplitude of the vibration table，which are used to control the vibration shaker.Also，it can be seen from Table 6，the excitation level in the fixture is less than the excitation level intheTable.Maybethereasonisthattheenergyisdissipated when transferring from the Table to the fixture.

Table 3 The first 6-order modal damping ratios of the uncoated beam obtaned by experiment

Table 4 The first 6-order natural frequencies of the composite beam obtained by experiment and linear calculation/Hz

Table 5 The 3rd order resonance frequency and the resonance region response under different excitation levels obtained by experiment

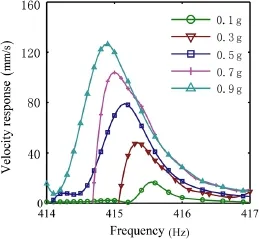
Fig.6 The 3-order sweeping response of composite beam under different exciting levels

5.2 Analytical calculation

To solve the 3rd resonance region responses and resonance frequency of the hard-coated beam，the number of considered modes was set as 6 during the process of analytical calculation.The strain dependent characteristic of hard coating is considered for the proposed method，so the solution process using the proposed method is called the nonlinear calculation.In contrast，if not considering the strain dependent characteristic，the solution process is called the linear calculation.To compare with the proposed method，the linear calculation was also done for the composite beam. For the nonlinear calculation，the convergence conditions were defined as TOL=1×10-6for the solution of vibration response and TOL=1×10-3for the calculation of resonance frequency，respectively.The iterative times of relevant calculations was 6 and 3，respectively.For the linear calculation，the material parameters of hard coating were taken as follows:storage modulus 50.439GPa and loss modulus 0.918GPa，which are corresponding to the 0 strain in Fig.1.The picking vibration point was consistent with experiment.Using these parameters，the natural frequencies and the 3rd order resonance response under different excitation levels were solved.The relative results are listed or shown in Tables 4，6，and Fig.7a，etc.It can be noted from the Table 4，the maximum difference of the first 6，order natural frequencies between the experiment and linear calculation is less than 3%，and the discussion about the other results can be found in the following section.

Then，considering the strain dependent characteristic of hard-coating material，the nonlinear calculation was done. The tested value in the fixture was chosen as the levels of base excitation.For convenience，the setting values，such as 0.1，0.3，0.5，0.7，and 0.9g，were still used to calibrate the excitationlevelsofthesysteminFig.7.Theremainingequivalent viscous damping can be introduced from Table 3.The calculation program was developed by Matlab and Maple software.The calculation result is also listed in Table 6 and Fig.7b.Because the material data in Fig.1 is only corresponding to the range of ε with（1-750）×10-6，so themaximum strain of the hard coating layer should be less than 750×10-6.For this calculation，the maximum strain is 179.457×10-6corresponding to the 0.61 excitation level，which is far less than the limited value.It can be seen from Fig.7 that the resonance response obtained by nonlinear calculation is less than the linear calculation value，which maybeprovesthatthestraindependentcharacteristicofhardcoating material is useful to improve the vibration reduction effect.

Table 6 The 3-order resonance frequency and resonance response under different excitation levels obtained by linear and nonlinear calculation

Fig.7 Frequency domain response of the composite beam near the 3rd order resonance region.a Linear calculation.b Nonlinear calculation

Table 7 The comparison of resonance response（mm/s）

5.3 Results comparison and difference analysis

Inthissection，thelinearandthenonlinearcalculationresults for the 3rd order resonance frequency and the resonance response were compared with the experimental values.The comparisonofresonanceresponseislistedinTable7andthe comparison of resonance frequency is listed in Table 8.

It can be seen from Table 7，the difference between the linear calculation of resonance response and the experimentbecomes bigger with the increase of excitation level.For example，when the excitation level is 0.1g，the difference of linear calculation is only 0.40%，and when the excitation level is 0.9g，the difference of linear calculation has been achieved as 16.42%.Compared with the linear calculation，the nonlinear calculation proposed in this study can always maintain an acceptable precision and the maximum difference with experiment is less than 7%.In addition，it can be noted that when the excitation level is very small，such as below 0.3g in this case，the linear calculation can acquire enough precision.For the resonance frequency calculation listed in Table 8，a similar conclusion can be drawn，that is，when the excitation level is bigger，the nonlinear calculation shouldbeadopted，althoughinthiscase，theprecisionofboth the linear and nonlinear calculation are acceptable.By the above comparison，the rationality of the calculation method considering the strain dependent characteristic of hard coating is verified.

Table 8 The comparison of resonance frequency（Hz）

6 Conclusions

On the basis of considering the strain dependent characteristic of hard coating，the dynamics modeling and analysis are studied，andsomeimportantconclusionsarelistedasfollows

（1）Using the higher order polynomial to characterize the material parameters of hard coating is an effective method.On the one hand，the higher order polynomial can describe the mechanical parameter change of hard coating with the strain amplitude；on the other hand，the mechanicalparametersexpressedbythepolynomialcan be easily introduced into the analytical model.

（2）The created analytical model and the solving method in this study can correctly solve the dynamics characteristics.The practice for the 3rd order calculation of the composite beam shows that the maximum difference of the resonance response calculation is less than 7%and themaximumdifferenceoftheresonancefrequencycalculation is less than 1.5%.

（3）The study shows that when the excitation level is low，such as less than 0.3g in the study case，the linear model canbeusedtosolvethedynamicscharacteristicsandcan maintain an acceptable precision.On the contrary，when the excitation level is bigger，the strain dependent characteristic of hard coating must be considered；using the nonlinear calculation is needed to acquire the dynamics characteristics of the composite structure.

（4）By comparison of the resonance responses obtained by linear and the nonlinear calculation，it can be found that theresonanceresponseobtainedbynonlinearcalculation is less than the result of linear calculation，which maybe means that the strain dependent characteristic of hard coating is good for the vibration reduction effect.

Acknowledgments ThisprojectwassupportedbytheNationalNatural Science Foundation of China（Grant 51375079）and the Fundamental Research Funds for the Central Universities of China（Grant N140301001）.

References

1.Yen，H.Y.，Herman Shen，M.H.:Passive vibration suppression of beamsandbladesusingmagnetomechanicalcoating.J.SoundVib. 245，701-714（2001）.doi:10.1006/jsvi.2001.3561

2.Shipton，M.，Patsias，S.:Hard damping coatings:internal friction asthedampingmechanism.In:ProceedingsoftheEighthNational Turbine Engine High Cycle Fatigue Conference 5e1-5e27（2003）

3.Patsias，S.，Tassini，N.，Lambrinou，K.:Ceramic coatings:effect of depositionmethodondampingandmodulusofelasticityforyttriastabilized zirconia.Mater.Sci.Eng.442，504-508（2006）.doi:10. 1016/j.msea.2006.04.129

4.Sun，J.，Kari，L.:Coating methods to increase material damping of compressor blades:measurements and modeling.ASME Turbo Expo:Power Land Sea Air 6，1157-1165（2010）.doi:10.1115/ GT2010-23790

5.Du，G.Y.，Ba，D.C.，Tan，Z.，et al.:Vibration damping performance of ZrTiN coating deposited by arc ion plating on TC4 Titanium alloy.Surf.Coat.Technol.229，172-175（2013）.doi:10.1016/j. surfcoat.2012.05.140

6.Torvik，P.J.，Henderson，J.P.:Influence of glass content on damping properties of plasma-sprayed mixtures of zirconia and glass. J.Mater.Eng.Perform.21，1405-1415（2012）.doi:10.1007/ s11665-011-0011-4

7.Hansel，J.E.:The Influence of Thickness on the complex modulus of air plasma sprayed ceramic blend coatings.Wright State University，Dayton（2008）

8.Torvik，P.J.:Determination of mechanical properties of non-linear coatings from measurements with coated beams.Int.J.Solids Struct.46，1066-1077（2009）.doi:10.1016/j.ijsolstr.2008.10.025

9.Reed，S.A.，Palazotto，A.N.，Baker，W.P.:An experimental technique for the evaluation of strain dependent material properties of hard coatings.Shock Vib.15，697-712（2008）.doi:10.1155/2008/ 853689

10.Tassini，N.，Lambrinou，K.，Mircea，I.，et al.:Study of the amplitude-dependentmechanicalbehaviourofyttria-stabilisedzirconia thermal barrier coating.J.Eur.Ceram.Soc.27，1487-1491（2007）.doi:10.1016/j.jeurceramsoc.2006.05.041

11.Ivancic，F.，Palazotto，A.:Experimental considerations for determining the damping coefficients of hard coatings.J.Aerosp.Eng. 18，8-17（2005）.doi:10.1061/（ASCE）0893-1321（2005）18:1（8）

12.Blackwell，C.，Palazotto，A.，George，T.J.，et al.:The evaluation of the damping characteristics of a hard coating on titanium.Shock Vib.14，37-51（2007）.doi:10.1155/2007/260183

13.Tassini，N.，Patsias，S.，Lambrinou，K.:Ceramic coatings:A phenomenological modeling for damping behavior related to microstructural features.Mater.Sci.Eng.442，509-513（2006）. doi:10.1016/j.msea.2006.04.140

14.Torvik，P.J.:A slip damping model for plasma sprayed ceramics. J.Appl.Mech.76，061018（2009）.doi:10.1115/1.3132182

15.Al-Rub Abu，R.K.，Palazotto，A.N.:Micromechanical theoretical andcomputationalmodelingofenergydissipationduetononlinear vibration of hard ceramic coatings with microstructural recursive faults.Int.J.Solids Struct.47，2131-2142（2010）.doi:10.1016/j. ijsolstr.2010.04.016

16.Green，J，Patsias，S.:A preliminary approach for the modeling of a hard damping coating using friction element.In:Proceedings of Seventh National Turbine Engine High Cycle Fatigue Conference（2002）

17.Reed，S.A.:Development of experimental，analytical，and numerical approximations appropriate for nonlinear damping coatings. Air Force Institute of Technology（2007）

18.Filippi，S.，Torvik，P.J.:A methodology for predicting the response ofbladeswithnonlinearcoatings.J.Eng.GasTurbinesPower 133，042503（2011）.doi:10.1115/1.4002272

19.Li，H.，Ying，L.，Sun，W.:Analysis of nonlinear vibration of hard coating thin plate by finite element iteration method.Shock Vib. 245，391-406（2014）.doi:10.1155/2014/941709

20.Patsias，S.，Saxton，C.，Shipton，M.:Hard damping coatings:an experimental procedure for extraction of damping characteristics and modulus of elasticity.Mater.Sci.Eng.370，412-416（2004）. doi:10.1016/j.msea.2003.07.020

21.Liao，Y.，Wells，V.:EstimationofcomplexYoung’smodulusofnonstiff materials using a modified Oberst beam technique.J.Sound Vib.316，87-100（2008）.doi:10.1016/j.jsv.2008.02.028

25 January 2016/Revised:14 March 2016/Accepted:21 March 2016/Published online:25 May 2016

✉W.Sun weisun@mail.neu.edu.cn

1School of Mechanical Engineering and Automation，Northeastern University，Shenyang 110819，China

2State Key Laboratory of Mechanical System and Vibration，Institute of Vibration，Shock and Noise，Shanghai Jiao Tong University，Shanghai 200240，China