城市天然气管网供应可靠性模型分析

姜好

（成都新都港华燃气有限公司，四川　成都　610500）

城市天然气管网供应可靠性模型分析

姜好

（成都新都港华燃气有限公司，四川成都610500）

当城市天然气日需求量大于天然气管网供给城市门站的日供气量时，用户用气得不到满足。针对这一问题，基于概率统计方法，得出城市天然气日需求量概率分布函数，假定管网供给门站的日供气量服从某种分布，建立管网供给门站的日供应—城市天然气日需求的干涉模型，推导出供应可靠度的表达式，并考虑到在计算可靠度时出现的管网供给天然气量和城市天然气日需求量的概率密度函数不可积的情况，引入蒙特卡洛模拟法得出供应可靠度。结果表明由蒙特卡洛模拟法得出的结果与可靠度计算公式所得结果近似相等，且模拟的次数越多模拟结果越精确。

长输天然气管网城市门站供应可靠度概率分布干涉模型

0　引言

干线管网供给门站的日供气量和城市的日需求量，是天然气供应程度具有不确定性的两个重要运行参数，可以通过供气量和需求量的概率分布来建立供应可靠度模型，采用结构可靠性方法计算供应可靠度［1］。管网供给城市门站的天然气量和城市天然气的日需求量的概率密度函数为特殊分布（正态分布、均匀分布、指数分布等）的情况下，可以通过查表来求得供应可靠度。然而实际观测数据的概率分布并非特殊分布，其干涉模型的供应可靠度需要用蒙特卡洛模拟法进行求解。为此，笔者拟就模型中的可靠度计算作一探讨分析。

1　天然气供给量—需求量干涉模型

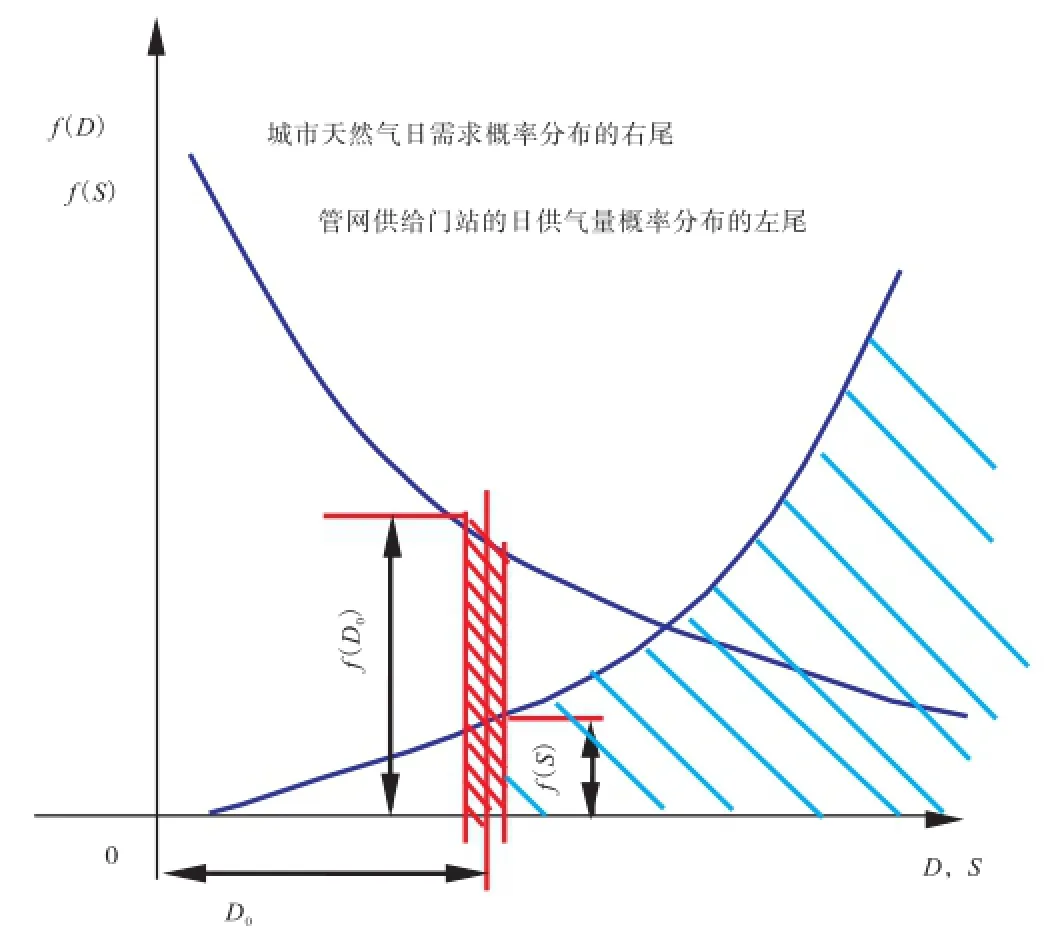
长输天然气管网供给城市门站的天然气量概率分布和城市天然气日需求量概率分布，可在同一坐标系中表示（图1），横坐标为气量（可同时表示管网供给天然气量和城市天然气需求量），纵坐标为概率密度函数（可同时表示管网供给天然气量概率密度函数f（S）和城市天然气日需求量概率密度函数f（D））。

图1　管网供给城市门站的天然气量—城市天然气需求量干涉模型图

图1阴影部分为管网供给门站的日供气量概率密度分布与城市天然气日需求量概率密度分布的尾部“干涉区”，它表明门站日供气量有可能小于城市日需求量，即可能处于“供小于求”的状态［2］。根据“干涉区”的分布特征，即可以建立门站“供小于求”的概率模型，称为管网供给城市门站的天然气量—城市天然气日需求量（S-D）干涉模型（类似于结构失效概率干涉模型）。需注意的是“干涉区”的面积不等于“供小于求”的概率［3］。

在管网供给城市门站的天然气量—城市天然气日需求量（S-D）干涉模型中，天然气管网供给城市门站的天然气量大于城市天然气日需求量的概率可表示为该门站的供应可靠度R（t）为：

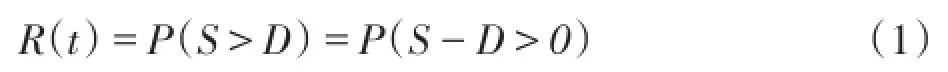
2　供应可靠度的表达式及计算

2.1一般表达式

根据图1的干涉模型，可以计算出供应可靠度。设城市天然气日需求量为D0，其干涉放大区见图2所示，管网供给城市门站的天然气量大于D0的概率为：

城市天然气日需求量D0处于dS区间内的概率为：

因为D0为城市天然气日需求量区间内的任意值，其可在（0，+∞）区间内取值，则管网供给门站的日供气量大于城市天然气日需求量的供应可靠度为：

当已知天然气日需求量和管网供给天然气量的概率密度函数时，根据上述模型即可求得门站的供应可靠度。

2.2供应可靠度的计算

当管网供给城市门站的天然气量和城市天然气日需求量的概率密度函数均为正态分布时［4］，有：

R（t）=P（S-D＞0）=P（Z＞0）（6）式中，Z为供求余量，Z=S-D。

由于两者的概率密度函数均为正态分布，根据正态分布的和（差）仍为正态分布的性质，供求余量Z也为正态分布：

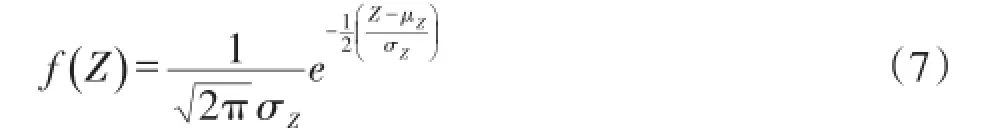
供应可靠度为：

上式可转化为标准正态分布形式：

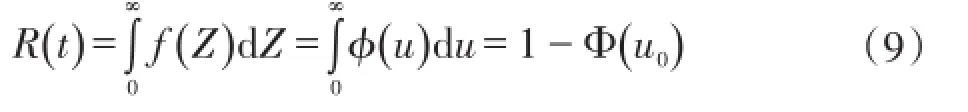
从式（9）可知，当已知管网供给城市门站的天然气量和城镇日需求量的分布参数后，就可计算出连接系数（可靠性系数）u0，供应可靠度可从正态分布表中查得。因此，式（9）把日需求量分布参数、管网供给天然气量分布参数和供应可靠度直接联系起来。

3　蒙特卡洛模拟法

蒙特卡洛模拟法的优点是：① 得到的数值比较精确；② 其方法受问题类型的影响较小［5］。因此只要知道管网供给门站的天然气量和城市天然气日需求量的分布情况，不管其分布为正态分布或是一般分布，都可以通过蒙特卡洛模拟方法来求解。

蒙特卡洛模拟法可以用来求解管网供给城市门站的天然气量和城市天然气的日需求量分布干涉情况下的供气可靠度。这种方法的实质是，从管网供给城市门站的天然气量的分布中随机选取一个日供应量值，并将其与取自城市天然气的日需求量分布的日需求量值进行比较，然后统计比较的结果，从而可以计算出供气可靠度［6］。图3为牟志忠等学者用蒙特卡洛模拟法进行可靠度计算的流程图［7］。

已知天然气管网供给城市门站的天然气量和城市天然气的日需求量分布都呈正态分布，其均值和方差分别为μS=700 120 m3，σS=4 844 m3，μD=604 230 m3，σD=51 388 m3，用蒙特卡洛模拟法计算供气可靠度［9］。根据蒙特卡洛模拟法计算可靠度的流程说明的步骤，编制matlab程序，所得出的模拟计算结果见表1。

图3　用蒙特卡洛模拟法计算可靠度的流程图

表1　蒙特卡洛模拟计算结果表

由可靠度计算公式所得的结果为0.968 4，与蒙特卡洛模拟结果对比可知，增加模拟次数可以提高模拟计算结果的精确度。

4　结论

1）根据管网供给城市门站的天然气量和城市天然气的日需求量的概率密度函数可建立管网供给天然气量—天然气日需求量的干涉模型。

2）根据可靠度的定义，得出干涉模型中供应可靠度的一般表达式，可以用于计算供应可靠度。

3）根据干涉区域内的系统处于不可靠状态，推导出供应可靠度的表达式。考虑到在计算可靠度时，管网供给城市门站的天然气量和城市天然气的日需求量的概率密度函数不可积的情况，引入了蒙特卡洛模拟法，结果证明增加模拟次数可以提高模拟计算结果的精确度，使其越来越接近于可靠度计算结果。

［1］张洪才.应力—强度干涉模型的可靠度计算方法的研究［J］.应用技术与实例分析，2001（6）：45-47.

［2］罗金恒，赵新伟，韩晓毅，等.西气东输管道可靠度预评估［J］.焊管，2005，28（3）：62-65.

［3］闰春宁.论可靠性工程中应力与强度分布干涉区的提法［J］.哈尔滨建筑工程学院学报，1989，22（4）：42-45.

［4］曾声奎，赵廷弟，张建国，等.系统可靠性设计分析教程［M］.北京：北京航空航天大学出版社，2000.

［5］王勇.普光输气站场定量风险评价技术研究［D］.成都：西南石油大学，2012.

［6］牟志忠，朱文予.机械可靠性设计［M］.北京：机械工业出版社，1993.

［7］牟志忠.机械可靠性：理论·方法·应用［M］.北京：机械工业出版社，2011.

［8］张思，周思柱，李美求，等.基于VB与Matlab混合编程的机械零件可靠性设计［J］.机械，2014，41（6）：44-48.

［9］张仙风，吕志鹏.基于MATLAB的蒙特卡罗方法在可靠性设计中的应用［J］.装备制造技术，2006（4）：76-77.

（编辑：蒋龙）

B

2095-1132（2016）04-0068-03

10.3969/j.issn.2095-1132.2016.04.019

修订回稿日期：2016-07-03

姜好（1989-），硕士，从事燃气风险管理工作。E-mail：jhswpu@126.com。