基于de Bruijn图的序列拼接算法研究与实现

李飞菲

（四川大学计算机学院，四川　610065）

基于de Bruijn图的序列拼接算法研究与实现

李飞菲

（四川大学计算机学院，四川610065）

0　引言

全基因组测序是生物信息学最为重要的研究方向，基因组记录了某个物种的全部遗传信息，测定基因序列（DNA序列）可以破解其中的信息，进一步了解各类生物，并为人类健康和物种发展带来实际意义。DNA序列由四种不同的碱基组成，即腺嘌呤 （A）、胞嘧啶（C）、鸟嘌呤（G）、胸腺嘧啶（T），它们按照特定的编码规则连接成链。基因测序就是为了测定DNA序列中碱基的排列顺序。

目前的测序技术一次实验测得的长度不超过1000个碱基对（bp）[1]，而普通高等生物基因中的碱基数目往往十分庞大，人类基因组的总长度就达到了30亿bp。因此，测序时首先将DNA序列复制成多份，然后将长序列打断成小序列片段（read），通过测序仪精确地测出每个read的碱基排序，然后利用序列拼接软件将read在计算机上拼接起来，恢复成原来的DNA序列中的一条或多条连续段（contig）[2]。在实际操作过程中，DNA序列可能会出现丢失、变异、重复等问题，对如此复杂的序列进行拼接，DNA序列拼接算法的重要性不言而喻。

本文对基于de Bruijn图的序列拼接算法进行研究，分析拼接过程中的每个阶段，并利用C++语言编程实现该算法，对运行实验结果进行分析，与Velvet拼接软件的结果进行对比。

1　序列拼接算法的研究现状

基于第一代测序技术的序列拼接方法适合处理长度为500-1000bp的read，利用read之间的重叠关系建立重叠图，这种基于重叠图的算法主要有三个阶段：（1）overlap阶段：将所有read进行两两比对，找到有重叠的read；（2）layout阶段：利用重叠信息建立重叠图；（3）consensus阶段：遍历重叠图，图中的每条路径都可能成为contig，将得到的所有contig进行组装，得到最后的拼接结果。

随着生物信息的飞速增长，生物组织中的多样性和关联性不断增强，传统的测序方法已经不能满足当下的需求。第二代测序技术面对的数据长度极短、数量庞大、覆盖度较高，最短的只有25-50bp，不适合建立重叠图。基于de Bruijn图的序列拼接算法是新一代测序技术最常用的方法，适用于拼接高通量的短read，已经被应用于各种序列拼接技术，如Velvet[3]、SOAPdenovo[4]、AbySS[5]等。它将read转化成一组连续的k-mer，然后寻找kmer之间的重叠关系，建立de Bruijn图，最后将问题转化为寻找欧拉路径问题。

2　de Bruijn图简介

假设给定的DNA序列集合是S={S1，S2,S3，…，Sn}，其中Si（1≤i≤n）表示一个长度为n的 read。对每个read，从头开始依次取出长度为k（1≤k≤n）的子串，该子串称为k-mer，一个read可以得到（n-k+1）个连续的k-mer，它的集合为K={k1，k2，…，kn-k+1}。

在de Bruijn图结构中，以k-mer作为节点，如果存在两个k-mer在read中相邻，即k1的后（k-1）个碱基与k2的前（k-1）个碱基重叠，那么图中对应的两个节点之间存在一条由k1指向k2的边。由于k-mer是根据read产生的，因此每一条read可以看作图中的一条路径。由此可以构建出一个以k-mer为基本单位的有向图，如图1所示。

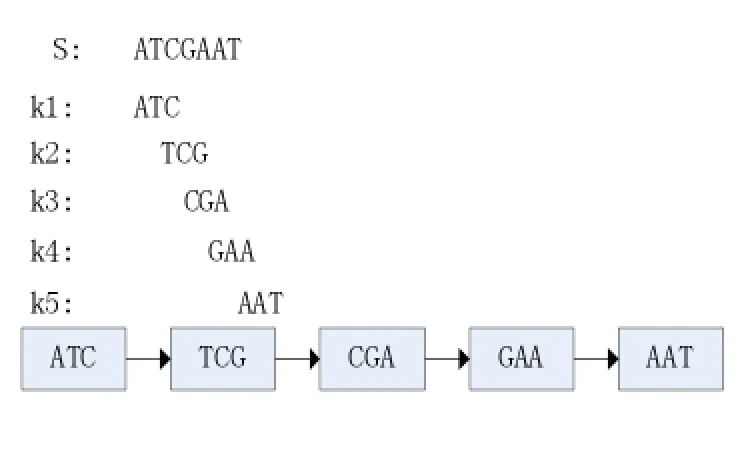
图1　de Bruijn图的构建过程

这样的结构可以保证每个k-mer在图中只出现一次，read之间所有的连接关系都被转化到了k-mer上。根据k-mer之间的重叠信息，寻找一条经过所有边一次且仅一次的路径，即可得到一个近似原DNA序列的拼接结果。

序列在处理过程中可能产生丢失、变异、重复等问题，会使de Bruijn图产生三种结构：Tips结构、Bubbles结构和Repeats结构。

Tips是因为read在边缘出现了错误，导致图中的路径在某一端产生分叉，这种结构会影响到图的遍历。如图2所示，当走到GAA节点时，无法确定接下来该去往AAT还是AAA。

Bubbles是因为read中间出现了错误，导致图中路径的开始节点和结束节点相同，但是中间的节点序列不完全相同，这种结构同样会影响遍历结果。如图3所示，当走到ATC节点时，无法选择出正确的路径。

图2　Tips结构

图3　Bubbles结构

Repeats其实不算是一种错误结构，它是由序列片段内部的重复产生的，会使de Bruijn图产生循环结构，无法确定遍历方向。如图4所示，当走到ATC节点时，由于重复区域TCG、CGA的存在，无法直接确定应该去往GAA还是GAT，走到TTC节点时也有同样的困扰。

图4　Repeats结构

这些结构会影响de Bruijn图的遍历，导致无法找到正确的路径，在实现拼接算法时应该进行相应的处理。

3　算法实现

基于de Bruijn图的序列拼接算法可以分为三个阶段：构建图、化简图、消除错误结构。

首先逐条处理read，按照指定的k-mer长度将read划分为一系列k-mer。为了保证序列拼接的完整性，对于每个k-mer求出其反向互补的k-mer’，比较两个k-mer的大小，将大的k-mer称为k-mer+。分别将两个k-mer存储到图中，以k-mer+所在节点为代表，任何对某节点的处理都会影响到它的反向互补节点（TwinNode）。然后根据该k-mer在read中与其他kmer的重叠关系，在节点之间建立有向边，如果节点A到节点B有一条有向边，那么反向互补节点B’同样应该有一条有向边指向A’。与此同时，还需要累计每个节点和每条边出现的次数，作为该节点或边的覆盖率，覆盖率越低表明这个节点越不可靠。

本文设计了三个数据类型，分别是节点Node，边Arc和图Graph。Node中存储了k-mer序列、覆盖率、边等信息，并且有一个指向TwinNode的指针；Arc中存储了节点的出边，用指针来指向下一个节点；Graph中含有一个以k-mer为索引的哈希表，存储了相应的Node信息。三者之间的关系如图5所示，从图中已经无法看出read之间的重叠关系，两个节点只通过一条边连接，这种结构消耗的内存少，而且搜索便捷。

图5　de Bruijn图的结构关系

经过对de Bruijn图的构建可以发现，图中的节点非常多，每个k-mer都是单独的一个节点，想要直接发现其中的关联非常困难，因此可以对图进行化简，从而使图中的结构更加清晰。当节点A只有一个出边指向节点B，并且B也只有一个来自A的入边，那么就可以把A和B两个节点合并成一个节点，同时合并它们的反向互补节点A’和B’。值得注意的是，节点与边的覆盖率也应该进行相应的合并。

化简图操作不会影响节点的信息，同时能够有效地减少内存占用。为了保证de Bruijn图一直保持最简，在消除错误结构时需要迭代的对图化简。

（1）消除Tips结构

首先设置一个大小为2kb的阈值，当Tips的长度小于阈值时才可以消除它。这个阈值远大于read的长度，因为Tips中包含的read越多，它的长度就越长，出错的可能性就越小。然后比较Tips节点与其他同源“兄弟节点”的覆盖率大小，如果没有比Tips的覆盖率更小的节点，那么说明其他路径都更加的普遍，是正确路径的可能性更高。如果以上两个条件都满足，直接删除该Tips节点即可。

（2）消除Bubbles结构

首先根据Bubbles结构的特点，使用Dijsktra广度优先算法，从任意节点出发，访问它所能达到的其他节点，优先访问快的那条边。从节点A到节点B所需的时间可以根据节点的长度和边的覆盖率计算得到，如公式1所示。

对访问过的节点进行标记，当遇到了已标记的节点时开始回溯，找出两条路径最近的共同祖先节点，记录下这两条路径。将这两条路径进行对齐处理，如果足够相似就将它们合并成一条，否则选择快的那条路径，因为消耗时间少的边覆盖率高，所以是正确路径的可能性更高。

（3）消除Repeats结构

首先从Repeats结构中的任意节点出发，确定该节点所在的read，将read中的节点进行标记，然后根据不同read在标记节点上的重叠情况扩展到下一个read，继续对后续节点进行标记，直到这个Repeats结构被处理完。最后将被标记的节点串连起来，可以得到一条确定的路径，消除Repeat结构产生的困扰。如图6所示，重复区域是节点C、D，首先从节点A出发进行标记，由于read1能够覆盖A和C两个节点，因此对C进行标记；然后从节点C出发，可以发现C还存在于read2中，而且read2覆盖了C、D、F三个节点，按照read2的路径继续进行扩展和标记；最后将被标记的节点串连起来，可以确定该Repeats结构的一种寻路方式为A→C→D→F。

图6　Repeats结构的解决方法

在消除以上几种错误结构后，可能还存在一些无法从图中直接识别出来的连接错误。设置一个覆盖率阈值，将小于这个阈值的节点全部删除，消除错误连接的影响。这个阈值的大小可以根据实际情况自定义。

以上全部操作完成后，再对图进行一次化简合并，可以得到若干条较长的序列片段，称为contig。一个contig包含多个k-mer甚至多个read。这些contig就是最终的拼接结果，根据实际需要还可以对它们做进一步的拼接处理，得到一个含有若干空隙（gap）的长序列，尽可能的还原到原始DNA序列。

4　结果分析

实验环境为处理器：Intel Core i3-3220 CPU@ 3.30GHz；内存：4.0GB；操作系统：Windows 7。

本文选取了三种不同规模的DNA序列模拟样本进行实验。Read长度为35，具体信息如表1所示。

表1　实验数据集信息

本文以contig片段在原始序列上的恢复率为衡量标准，判断算法的正确性与可行性。假设原始DNA序列长度为L，拼接算法得到的contig个数为n，每个contig的长度为ci（1≤i≤n），其中拼接错误的contig总长度为X，那么算法的恢复率如公式2所示。

由于gap的存在，contig的恢复率很难达到100%，为了有效地验证实验结果，本文使用Velvet算法运行相同的实验数据，将得到的结果进行对比分析。K值为21，实验结果如表2所示。

表2　实验结果

从当前的实验数据来看，本文算法得到的contig长度较长、正确率较高，与Velvet的恢复率相差不大，可以证明本文中的算法是正确的、可行的。

5　结语

本文基于de Bruijn图，设计了一种数据结构，通过化简、消除错误结构等操作对短基因序列进行拼接，并且得到了与原始序列很相似的拼接结果。但本文也存在一些不足之处，对错误结构的处理不够全面，在一定程度上影响了最终寻路的正确性，导致无法获得更长更连续的contig，因此在消除错误结构的算法上还需要继续研究和改善。

[1]骆志刚等.DNA序列拼接的研究和挑战[J].计算机工程与科学,2007.

[2]王旭.基于deBruijn图的DNAcontig生成算法[D].哈尔滨工业大学:王旭,2011.

[3]Daniel R.Zerbino,Ewan Birney.Velvet Algorithms for de Novo Short Read Assembly Using de Bruijn Graphs[J].Genome Res,2008.

[4]Li R,Zhu H,Ruan J,et al.De Novo Assembly of Human Genomes with Massively Parallel Short Read Sequencing.GenomeRes，2010.

[5]Simpson JT,Wong K,Jackman SD,et al.ABYSS:A Parallel Assembler for Short Read Sequence Data[J].Genome Res,2009.

Next-generation Sequencing Technology;High-throughput Sequencing;DNA Sequence Assembly;de Bruijn Graph

Research&Implementation of Sequence Assembly Algorithm Based on de Bruijn Graphs

LI Fei-fei
（College of Computer Science,Sichuan University，Sichuan 610065）

1007-1423（2016）02-0003-05

10.3969/j.issn.1007-1423.2016.02.001

李飞菲（1991-），女，北京人，本科，研究方向为计算机图形学、虚拟现实

2015-11-24

2015-12-28

序列拼接算法是DNA测序过程中的关键技术。随着新一代测序技术的发展，如何实现高通量、高效率测序已经成为生物信息学领域的重要挑战，序列拼接算法也在逐渐改进以提高拼接效果。基于de Bruijn图的序列拼接算法是目前使用最广泛的方法之一，对其进行分析研究，利用C++编程实现该算法，并对实验结果进行分析。

新一代测序技术；高通量测序；基因拼接；de Bruijn图

Algorithms for DNA sequence assembly are the key process of gene sequencing.With the development of next-generation sequencing technologies,how to achieve high-throughput,high-efficiency sequencing has become an important challenge in bioinformatics.At the same time,sequence assembly algorithms also have been improved to get better results.The algorithms based on de Bruijn graph are the most popular DNA sequence assembly algorithm,analyses and researches on it,applies C++language to program this algorithm,and analyses the experiment results.