声辐射力成像位移计算改进方法

尤鑫

（四川大学医学影像实验室，成都　610065）

声辐射力成像位移计算改进方法

尤鑫

（四川大学医学影像实验室，成都610065）

0　引言

医学超声振动性弹性成像（Vibration Sonoelastography）由Fatemi和Greenleaf于1998年发明。该技术是用一个超声波场产生一个低频振动并作用于受检组织，组织受到激励根据自身的弹性模量大小产生不同的振动幅度，并最终通过图像表现出来[1-2]。采用声辐射力的声辐射脉冲成像属于振动性弹性成像的一种，ARFI成像测量组织的反应是通过使用由长脉冲引起的声辐射力产生局部位移从而深入探察在有机体体内和体外的软组织局部粘弹性性能[3-4]。位移检测是ARFI成像中最为重要的环节，是组织生物力学特性分析的基础。传统的方法通常采用胡相关方法，迭代相位零（Iterative phase zero）方法或者loupas算法，组织位移的估算可以通过对激励之前（参考）和激励之后（跟踪）信号进行计算获得[5]。Loupas算法提供了一种对轴向速度推导得到的速度估算，它是通过利用显示估计在每个距离选通脉冲位置的平均多普勒频率与平均射频频率来转换多普勒方程式[6]。Loupas结合了一般的较高性能的2D宽带时域技术与有相对温和复杂性的1D窄带相域并满足被提出的估算函数计算要求的速度估算函数。

现有医学超声声辐射力成像一般采用Loupas算法得到由声辐射力引起的微小位移。而在传统Loupas算法中，计算位移时通常只选取初始时刻和之后的各个不同时刻的采样点来进行绝对位移的计算，这种计算方式在时间方向的窗口N为2，容易受噪音影响，使位移曲线不够连续和平滑。具体而言，由于N取值小，回波相位位移计算时间短，包含信息少，计算误差大，从3节位移曲线可看出，计算结果抖动较大，导致最后成图效果不佳；而当N取值过大时，回波相位位移计算时间长，且由于包含过多冗余信息，而导致计算结果不准确，成图效果变差，因此本文通过在成像过程中比较作用于模型焦点位置的回波信号不同时间取样窗口大小，研究不同时间取样窗口的大小下，焦点位置的不同的回波位移-时间曲线，选择出最适时间取样窗口取值，将优化后的参数反馈给系统从而取得更好的成像效果。

本文着重比较了成像处理过程中在焦点区域不同时间取样窗口下的回波位移-时间曲线，选择合适的时间取样窗口大小的值，并反馈优化后的参数到系统中，从而获得更好的成图效果。

1　研究方法

1.1Loupas算法介绍

复杂解调信号z（m，n）下2D自相关器获得的平均速度[7]：

其中γdem是z（m，n）的2D自相关函数；

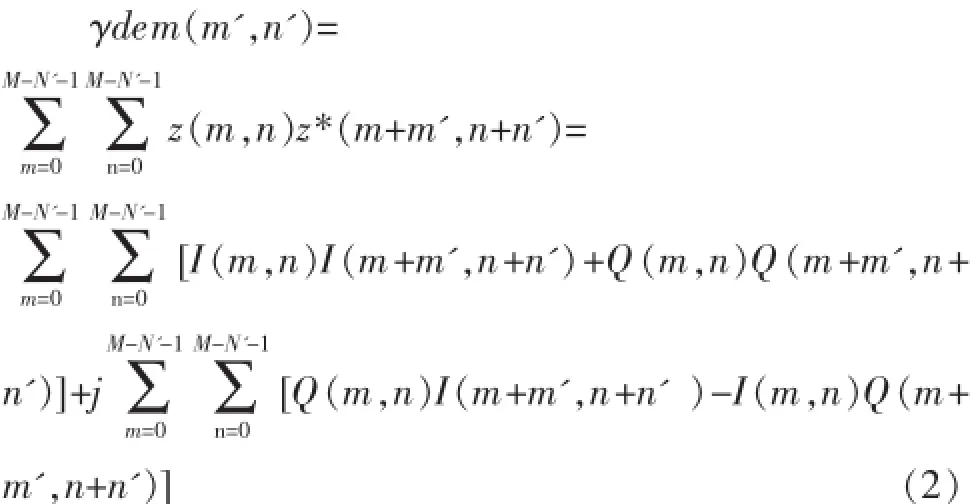
最后，依据I＆Q采样，公式（1）和 （2）可以结合来表示平均速度，如公式 （3）：

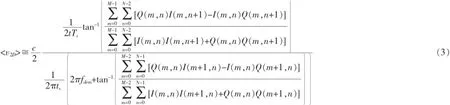
1.2平均位移计算

在涉及使用Loupas算法计算ARFI位移的先前文献中，时间取样窗口N通常取值为2，计算位移时，由激励脉冲产生的回波信号由于受到发射长波造成的干扰而没有计算价值，因此会将其去除，且以与参考脉冲对应的回波信号为基准，分别与剩余的检测回波信号进行计算。

由于要改变时间取样窗口，且需保证计算中的每个回波信号在时间方向的间隔保持一致，因此在位移计算前，需要对回波信号进行重采样。本文采用的是线性插值法，分别采用相邻检测脉冲对应的回波信号进行线性插值替换3组激励脉冲对应的回波信号；并利用公式（3）并改变式中N的取值来分别计算相邻的回波在时间取样窗口N内的平均位移速度。之后，运用公式（5），（6）计算出回波在时间方向的具体位移：

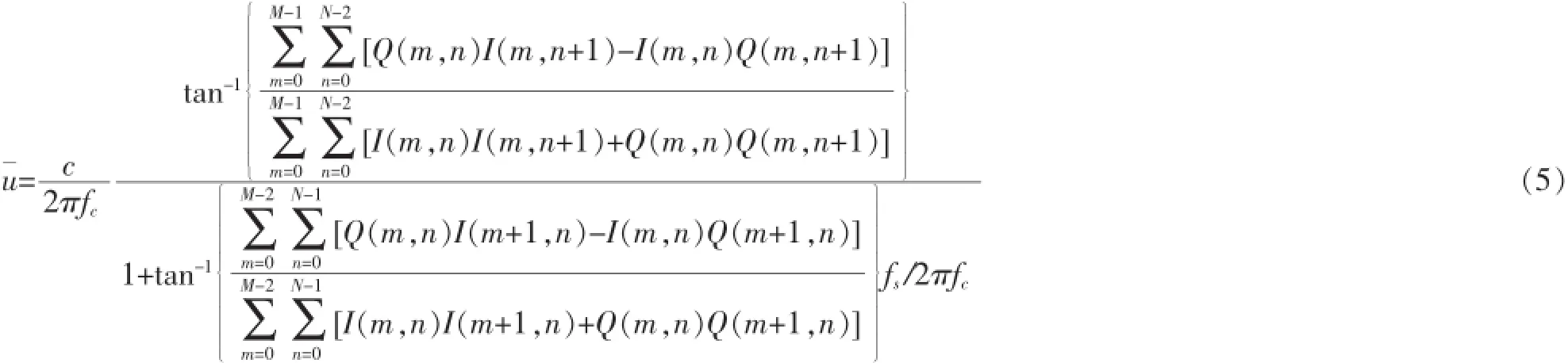
其中ui为组织时间方向对应的局部位移，fc是信号中心频率，fs是采样频率，di为被测组织在时间放向对应的局部位移，TPRF为脉冲重复周期，i的取值范围为0到取样容积数之间，d0为初始时刻，因为没有声辐射力的激励，所以d0=0。

2　实验与结果

二维的ARFI图像由多个扫描位置计算得到，它们之间间隔0.5mm，且具有相同的焦点深度。接收到的检测信号与参考信号通过使用Loupas算法进行相关性计算得到由声辐射力引起的微小位移。

在声辐射力检测过程中，首先发射的脉冲作为位移计算的参考信号，信号使用较高的电压和较短的脉冲长度，接下来发射了3组激励脉冲和检测脉冲。单脉冲序列中包含有参考检测脉冲、激励脉冲（长脉冲）、检测脉冲（短脉冲），回波信号中具有与上述脉冲一一对应的回波信号。扫描包的大小为24，脉冲序列的示意图见图1。

图1　脉冲序列的示意图

实验数据采集时，探头中心频率为5MHz，采样频率为40MHz，重复频率为8.88kHz，取样容积数为24。实验采用CIRS公司的Model049模型，模型由4种力学特征不同的球形组织和弹性背景组织构成，类型1-4的弹性系数依次为：8kPa，14kPa，45 kPa，80 kPa，背景区域为25 kPa。本实验采用类型1弹性系数为8 kPa的小球进行声辐射力激励与回波检测。

２.1位移曲线

本实验的取样容积数为24，所以自相关算法时间取样窗口N的取值范围为2≤N≤24，由于N取值过大，会加入多余信息干扰实验结果并影响计算效率，所以本实验只选取了2≤N≤10，9组数值进行研究考察，由于N取值相近时结果相差不大，因此本文只选取了原Loupas算法、N取值为4，6，8的结果进行展示。通过第二节中的算法分析，利用本文提出的自相关Loupas算法的改进，由公式（5）可计算得到在实验环境下所选ROI内位置由声辐射力引起的微小位移。由于ARFI成像技术只在焦点区域能量最强、信息最为准确，且为了方便研究声辐射力所引起的位移规律，本文根据公式（7）选择了焦点有效区域位置内的点进行线性平均计算并显示其回波位移-时间曲线。

其中rD为焦点有效区域边长，f#为震源深度与孔径宽度之比，λ为波长，本实验中f#=1.5，因此rD为0.14cm。

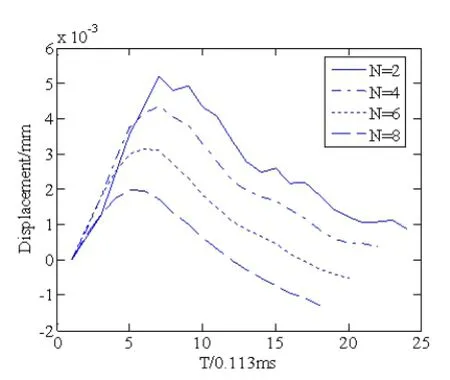
图2　焦点有效区域回波位移-时间曲线

图2为原Loupas算法与改进算法不同时间取样窗口大小（N=4，6，8）下焦点有效区域的平均回波位移-时间曲线图。由于原算法中，激励脉冲所对应的回波无效被删除，所以位移曲线中本文使用线性插值的方法将3个回波所对应的位移值插出。由图可知，在相应的取样容积数目（Ensemble size）下，小球的运动情况均为从静止运到到一定位移，最后归于平衡。而随着N的值地不断增加，位移曲线也更加平滑。

由第2节可知利用Loupas算法计算出的结果为回波在时间取样窗口内的平均位移速度，而当位移出现负值时，说明小球往反向运动从而产生了位移；然而小球在取样容积数目范围内，延时间方向，应趋于平衡，而非向负向发生位移，从原算法所计算出的时间-位移曲线图可以看出，在时间最末小球位移趋于0，为非产生负向位移。因此，当位移出现负值时，说明时间取样窗口过大，计算位移速度时包含过多信息，且延时间方向向后的信息信噪比低，导致计算出的反向平均速度过大且不准确，从而产生负向位移，使得最终计算结果不准确。

所以，当位移曲线中出现负值时，说明N选取过大，使得计算结果不准确，最终降低了成图效果。由图2可知，当N=4时曲线平滑度较高，且在其相应的最后时刻，小球位移趋于0（小球趋于平衡），未产生负向位移，为最合适的取值，成图效果为最佳。

２.2MSATLAB仿真成图与性能参数比较

本文对不同的时间取样窗口大小，选择其相应的取样容积范围内，小球位移达到最大值的时刻成像，而非像现有的医学超声声辐射力成像一般提供的固定时刻位移成像，并与原Loupas算法的成像结果进行比较，仿真成像结果如图3所示。

由图3可以看出，当N取值较小时（原算法），成图效果不佳；当N取值过大后，成图效果没有随着N的取值增大而线性改善，反而成像效果逐渐变差;可看出当N取值为4时，成图效果最佳。

为进一步确认是否Loupas时间取样窗口为4时，成图效果最佳，本文对所成图像利用公式（8）进行CNR[8]计算与比较：

图3　Loupas算法仿真成像与改进后不同时间取样窗口对应仿真成像

其中μt与σt分别表示目标区域应变的均值与标准差，μb与σb分别表示背景区域应变的均值和标准差。

本文以球内的区域为目标区域，球外的4个区域分别为背景区域，分别计算出相应的CNR，再将4个CNR进行平均（5个区域范围大小几乎相等），如图4:

图4　CNR计算区域选择示意图

结果如表1所示。

表1　各仿真图像的CNR值

从表1可以看出，时间取样窗口为4时，CNR值最高，再次证明4为最佳值。

3　结语

本文研究声辐射力的成像算法问题，对声辐射力成像现使用的Loupas算法进行了改进，利用焦点位置区域中心的时间-位移曲线选取合适的算法时间取样窗口的值，达到更好的成像效果。

由于现使用的Loupas算法中，时间取样窗口N取值为最小值2，N取值小，回波相位位移计算时间短，计算误差大，因此本文对此进行了改进，并研究N的最佳取值。在观察计算得出的不同时间取样窗口大小下焦点有效区域内的平均回波位移-时间曲线图后分析发现，当N取值增加到一定值时，位移出现负值时，说明小球往反向运动从而产生了位移，与小球在取样容积数目范围内，沿时间方向，最后时刻应趋于平衡，而非向负向发生位移相悖，说明此时N取值过大，受过多信息干扰，使得计算结果不准确，最终降低成图效果。最终根据不同时间取样窗口大小下焦点有效区域内的平均回波位移-时间曲线图分析，MATLAB仿真成图效果以及CNR计算比较，得出时间取样窗口N取值为4时，成图效果最佳。

采用本文提供的基于声辐射力的回波位移检测方法，可以有效选取位移检测过程中的时间取样窗口，使位移检测可靠性更高，成图效果更好，对改进现有医学超声声辐射力成像系统，为医生诊断提供更准确结果显示具有一定意义。本文研究只针对激励脉冲数为3，较为局限，后续工作中要进一步对不同的激励脉冲数对应的时间取样窗口大小最佳取值进行研究，进行自适应地调整位移检测过程中时间取样窗口。

[1]M F，JF.G.Vibro-Acoustography:an Imaging Modality Based on Ultrasound-Stimulated Acoustic Emission.[J].Proc Natl Acad Sci U S A，1999，96（12）:6603-6608.

[2]Fatemi M，Greenleaf J F.Ultrasound-Stimulated Vibro-Acoustic Spectrography[J].Science，1998，280（5360）:82-85.

[3]K N，R B，G.T.Observations of Tissue Response to Acoustic Radiation Force:Opportunities for Imaging[J].Ultrasonic Imaging，2002，24（3）:129-138.

[4]Nightingale K，Soo M.Acoustic Radiation Force Impulse Imaging:in Vivo Demonstration of Clinical Feasibility[J].Ultrasound in Medicine&Biology，2002，28（2）:227-235（9）.

[5]JR D，GE T，KR N，et al.Acoustic Radiation Force Elasticity Imaging in Diagnostic Ultrasound.[J].IEEE Trans Ultrason Ferroelectr Freq Control，2013，60（4）:685-701.

[6]Loupas T，Powers J T，Gill R W，et al.An Axial Velocity Estimator for Ultrasound Blood Flow Imaging，Based on a Full Evaluation of the Doppler Equation by Means of a Two-Dimensional Autocorrelation Approach[J].Ultrasonics Ferroelectrics and Frequency Control，IEEE Transactions on，1995，42（4）:672-688.

[7]Loupas T，Gill R W.Multifrequency Doppler:Improving the Quality of Spectral Estimation by Making full use of the Information Present in the Backscattered RF Echoes[J].Ultrasonics，Ferroelectrics and Frequency Control，IEEE Transactions on，1994，41（4）: 522-531.

[8]Shaoguo Cui and Dong C.Liu，Noise Reduction for Ultrasonic Elastography Using Transmit-Side Frequency Compounding:A Preliminary Study，IEEE Trans Ultrason Ferroelec Freq Control，2011，58，3.

ARFI;Elasticity Imaging;2D Autocorrelator Algorithm;Sampling Time Window

An Improved and Estimated Displacement Algorithm for Acoustic Radiation Force Impulse Imaging

YOU Xin
（Medical Imaging Lab，Sichuan University，Chengdu 610065）

1007-1423（2016）02-0068-05

10.3969/j.issn.1007-1423.2016.28.016

针对超声声辐射力成像中使用的传统Loupas算法计算误差较大，成像效果不佳的问题，提出一种改进方法。该方法在Loupas算法基础上，提出通过改变时间取样窗口大小，并利用二维自相关计算平均速度，进而得到更为准确的位移计算结果。实验结果与传统Loupas算法相比，提高弹性图像对比度噪声比，有更好的成像效果。

超声辐射力；弹性成像；二维自相关算法；时间取样窗口

With the purpose of solving the issue that there are errors in the traditional Loupas algorithm used in ARFI and the effects of imaging are not as good as expected,proposes an improved method to solve this proplem.Based on Loupas algorithm,it is presented that we can get more accurate computing result of the displacement by changing the size of the sampling time windows and calculating the average speed according to the 2D autocorrelator.As a result,not only improves Elastographic Contrast-to-Noise Ratio,but also the image quality.