高阶常系数齐次线性微分方程的解法
凯歌
(内蒙古财经大学统计与数学学院,呼和浩特 010070)
高阶常系数齐次线性微分方程的解法
凯歌
(内蒙古财经大学统计与数学学院,呼和浩特010070)
0 引言
求解常微分方程的问题,常常通过变量分离、两边积分,如果是高阶微分方程则通过适当的变量代换,达到降阶的目的来解决问题。本文是对几种类型的高阶常系数齐次线性微分方程的不同解法进行总结,分别对常系数齐次线性微分方程和欧拉方程、可降阶的高阶微分方程给出定义,应用变量替换法解齐次微分方程,降阶法求高阶微分方程,并且用具体的实例分析了常微分方程的应用。
1 基本方法的归纳总结
1.1常系数齐次线性微分方程和欧拉方程
(1)常系数齐次线性微分方程
定义设齐次线性微分方程中所有的系数都是常数,即:

这里的a1,a2,…,an代表常数。式(1)就被称作是n阶常系数齐次线性微分方程。
用通解的解法能够得出:


其中F(λ)=(λn+a1λn-1+…+an-1λ+an)是的n次多项式。所以x=eλt为方程(2)的充要条件是λ是:

的根。因此,式(2)是式(1)的特征方程,式(2)就叫做特征根。下面种常见情况分别进行讨论。
①特征根是单根的情形
设λ1,λ2,…,λn,代表特征方程(2)的n个不等根,所以相应的式(1)有n个解:

若λi(i=1,2,…,n)是实数,那么式(3)是式(1)的n个线性无关的实值解,而式(1)的通解可写成x=c1eλ1t,c2eλ2t,…,c3eλnt,其中c1,c2,…,cn是任意的常数。
如果出现复根,那么因为方程是实常数的系数,复根会以共轭形式成对的表达。如果λ1=α+βi是一个特征根,那么λ1=α-βi就也是特征根,式(1)的复值解。

因为实部和虚部也是方程的解,所以有两个实值解eatcosβt,eatsinβt
解 有特征方程λ4-1=0的根是λ1=1,λ2=-1,λ3=i,λ4=-i有两个实根和两个复根,都是单根,方程的通解x=c1et+c2e-t+c3cost+c4sint,这里c1,c2,c3,c4是任意的常数.
②特征根有重根的情形


先设λ1=0,即特征方程有因子λk,于是an=an-1=…= an-k+1=0,也就是特征方程的形为λn+a1λn-1+…+an-1λ=0。而式(1)变成可知它有k个解1,t,t2,…,tk-1且线性无关。所以特征方程的k重零根就对应于方程(1)的k个线性无关解1,t,t2,…,tk-1。如果这个k重根k≠0,作变量变换x=yeλ1t后,

其中b1,b2,…,bn仍为常数,而相应的特征方程为:

直接计算可得F(μ+λ1)e(μ+λ1)t=L[e(μ+λ1)t]=L1[eμt]eλ1t=G(μ)e(μ+λ1)t,所以F(μ+λ1)=G(μ),从而Fj(μ+λ1)=Gj(μ),j=1,2,…,k。可见式(2)的根λ=λ1对应式(5)的根μ=μ1=0,且它们重数相同。这样,问题就转化成前面讨论过的情形了。
解有特征方程λ3-3λ2+3λ-1=o,其中λ=1是三重根,所以方程的通解有形为:
x=(c1+c2t+c3t2)et,其中c1,c2,c3,表示任意常数。
(2)欧拉方程
定义 形如

的方程叫做欧拉方程,这里a1,a2,…,an为任意的常数。可通过变量变换转化为常系数齐次线性微分方程。
引进变换x=et,t=lnx,计算可得到:

其中β1,β2,…,βk-1为任意常数。于是:

把上面的式子代进式(6)后,就有:

其中b1,b2,…,bn为任意常数,所以可以求出上面的通解,再代回原来的变量(t=ln|x|),就可以求得方程(6)的通解。
解 设y=xK,得到K应该满足的方程K(K-1)-K+ 1=0,K1=K2=0。所以通解形式为y=(c1+c2ln|x|)x,其中c1,c2表示任意的常数。
1.2可降阶的高阶微分方程
定义 n阶微分方程一般地可以写

n≥2的时候,叫做高阶微分方程。与一阶方程的通解类似,一般的n阶微分方程(7)的通解都有n个任意的常数。求解高阶微分方程的途径,通常为通过变量变换使它降低阶数。现分为以下几种类型进行讨论。
(1)不显含未知函数x的方程
不显含未知函数x的方程,或者不显含未知函数和其直到k-1(k≥1)阶导数的方程,它的通常形式为:

易知,若x(k)=y,就化为关于y的n-k阶方程式:

阶数低的比阶数高的更容易求解。求出了(9)的解y=φ(t),就得x(k)=φ(t)。再积分k次,就能得到(8)的解。

1x=c1t5+c2t3+c3t2+c4t+c5,其中,c1,c2,c3,c4,c5为任意常数。
(2)不显含自变量的方程
一般形式有:



例5求解方程xx''+(x')2=0

设方程

的左端是关于变量x,x',…,x(n)的m次齐次函数,即对任何k≠0成立着恒等式
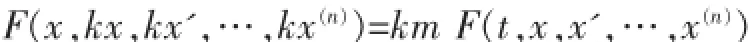
此时,方程(12)可写为:

或写为:



例6求解方程xx''-(x')2=0。

即y'=0或者y=c1,亦即x'=c1x。所以解为x=c2e (c1)。
2 结语
以上是对常微分方程中几类高阶常系数齐次线性微分方程的解法技巧的总结,希望学生通过各种类型方程的解法进行归类,并正确而又快捷地判断所给出的方程属于何种类型,从而按照所掌握的方法可以有条理地进行求解。但是不应该死记一些解法,更重要的是训练自己思维方法。
[1]王高雄等.常微分方程(第三版)[M].高等教育出版社,北京,2006.
[2]崔梅平等.常微分方程(第二版)[M].高等教育出版社,北京,1982.
[3]金富临等.常微分方程(第一版)[M].上海科学技术出版社,上海,1984.
[4]秦化淑.常微分方程及其应用(第一版)[M].国防工业出版社,北京,1985.
[5]任永泰、史希福主编等.常微分方程及其应用(第一版)[M].辽宁人民出版社,辽宁,1984.
[6]钱祥征等.常微分方程解题方法(第一版)[M].湖南科学技术出版社,湖南,1984.
[7]伍卓群、李勇等.常微分方程(第一版)[M].高等教育出版社,北京,2004.
Differential Equation;Characteristic Equation;Euler Equation;Homogeneous Equation
High Order Constant Coefficient Linear Differential Equation Solution
KAI Ge
(College of Statistics and Mathematics,Inner Mongolia University of Finance and Economics,Hohhot 010070)
1007-1423(2016)02-0026-04
10.3969/j.issn.1007-1423.2016.02.006
凯歌(1981-),女,内蒙古呼和浩特人,硕士研究生,讲师,研究方向为应用数学、经济动力学
2015-11-24
2015-12-24
常微分方程是微积分学的重要组成部分,求解高阶微分方程是常微分方程的一难点问题,通常用适当的变量代换,达到降阶的目的来解决问题。结合多年的教学经验,归纳总结给出高阶常系数齐次线性微分方程的一些求解方法,包括常系数齐次线性微分方程和欧拉方程以及可降阶的高阶微分方程等,并通过例题阐述各种方法。
微分方程;特征方程;欧拉方程;齐次方程
Ordinary Differential equation is an important part of differential and integration.Solving Ordinary Differential equation of difficult problem is the differential equations of high order.Generally,in order to achieve the purpose to solve problems,it uses an appropriate variable substitution.With many years of teaching experience,summarizes to give some methods for solving the linear differential equation of higher-order,including homogeneous linear differential equation with constant coefficient,Euler equations and higher-order differential of reduce order and so on,gives an example to explain a variety of methods.

