矩阵向量相乘并行算法分析与实现

郝 静 刘雅坤

中国石油大学（华东）理学院

矩阵向量相乘并行算法分析与实现

郝 静 刘雅坤

中国石油大学（华东）理学院

矩阵运算是工程数值计算中一种常见的运算方式。大量的高维矩阵运算对数学计算提出了新的要求。本文针对行划分，列划分不同模式，给出OpenMPI算法的分析与实现，并得到按行划分的优势。

矩阵向量，并行，OpenMP；

一、问题背景与提出

矩阵向量相乘是数学以及工程中经常遇到的一种计算方式，矩阵向量乘法在许多解决实际问题中都有应用，但矩阵计算因其维数增大而造成的计算量增大是计算科学中需要进一步解决的问题。利用并行计算方法，将矩阵向量进行分发，使每个进程同时进行计算，将会大大减少计算的时间，提高计算效率。

并行计算（Parallel Computing）是指同时使用多种计算资源解决计算问题的过程，是提高计算机系统计算速度和处理能力的一种有效手段。它的基本思想是用多个处理器来协同求解同一问题，即将被求解的问题分解成若干个部分，各部分均由一个独立的处理机来并行计算。现实社会中，越来越多的数据信息需要计算机处理，串行计算机程序技术已经不能满足人们的需求，并行计算会越来越受到人们的青睐。

从一个串行程序得到一个并行程序的工作一般由四个步骤构成：1）将计算分解成任务：分解的主要目标就是要揭示足够的并行性，从而尽量保持所有的进程在所有时间都忙，同时要注意由此引起的任务管理开销不能太大。2）将任务分配给进程：分配的基本性能目标是在进程之间做负载平衡，要减少进程之间的通信量，还要减少运行时管理这种分配的开销。3）在进程之间协调必要地数据访问、通信和同步。4）将进程映射或绑定到处理器。本文就是将矩阵与向量相乘分解成向量与向量相乘，分发给几个进程分别计算，将其并行化。

二、矩阵向量的串行算法描述

矩阵向量乘法是将一个mxn的矩阵A= （0≤i≤m-1，0≤j≤n-1）乘以nx1的向量B=得到一个具有m个元素的列向量C=。矩阵向量串行算法假设一次乘法和加法运算时时间为一个单位时间，则矩阵向量乘法算法的时间复杂度为O（mn），如果矩阵是方阵，那么复杂度就变为O（）。

矩阵向量串行算法：

三、模型建立

矩阵并行计算时，将矩阵进行按行、列、块三种方式进行划分，矩阵和向量按进程个数进行分发，接收矩阵和向量的进程做相应的运算，最后将结果进行规约综合。本文只讨论进程个数恰能完全将矩阵向量平均分配的情况。

通过已有相关文献的查阅，我们得知三种分法方式中，随着维数的增高，按行划分是最有效的方法；按列划分在分发时需要分发的次数为维数的倍数，分发的时间将大大增加。按块划分需要将矩阵进行块划分，按块划分的优势在矩阵与矩阵相乘的算法设计中优势比较明显。

在本文中，作者通过设计按块划分矩阵与向量相乘算法中发现，算法与按行、按列算法设计有很大的相似之处，所以，本文将着重考虑矩阵与向量相乘的按行与按列两种算法并行的情况。

3.1按行划分矩阵

矩阵向量相乘时，我们考虑nxn维矩阵A在n个进程间划分的情况。将计算机进程编号为0，1，2…n-1。则每一个进程都会存储1xn维矩阵。进程会存储ai1，ai2，ai3…ain。并且负责计算。向量C的存储方法与B相同。

考虑P（p＜n）个进程的情况，每个进程存储1×n/p维矩阵，每个进程的矩阵要与向量B相乘，所得的向量C与向量B的乘法类似。所得到的向量即为所求。通信时间为O（n/p），计算时间为O（n2/p）。

3.2按列划分矩阵

按列进行划分是对每一行进行划分然后发送到每个进程上。我们考虑n×n维矩阵A在n个进程间划分的情况。将计算机进程编号为0，1，2…n-1。对于矩阵的第一行，a11…a1n进行划分，进程pi接收到元素的为a1i，每一行划分后，进程pi接收到的元素为a1i…ani。进程pi做的计算为cj=aji×bj，j=1…n每一个进程都会得到一个向量，将每一个向量所对应的元素相加，即得到最终的向量c。

3.3按块划分矩阵

假设p2等于n，将矩阵划分成不同的矩阵块，每一个矩阵块上的矩阵为p×p维。将划分的矩阵块发送到每一个进程，进程上进行p×p维矩阵与的乘法运算。然后将计算同一行的矩阵块的进程结果相加，于同一列矩阵块相组合，得到最终的结果。

四、矩阵向量的并行算法描述

4.1基于OpenMP的多核并行算法的设计

OpenMP是一种面向共享内存以及分布式共享内容的多处理器多线程进行编程语言，是一种能够被应用于显式指导多线程、共享内存并行的应用程序编程接口。OpenMP具有良好可移植性，支持多种编程语言。OpenMP的编程模型以线程为基础，通过编译指导语句来显式地指导并行化，常用编译指导语句有parallel、parallel for、parallel sections，通过特定的#pragma omp进行标示。

利用parallel进行并行的原理是编译时将同一段代码复制到每一个线程上编译，然后在本线程上执行编译好的程序。所有线程程序相同，但是执行效果不同，比如利用OpenMP封装的内置函数omp_ get_thread_num（）来获得线程号，然后根据线程号完成不同任务。执行原理和WinAPI利用线程号相同，都是获取线程号来分不同任务，只不过线程号获取方式不同。利用编译指导语句parallel执行并行计算是粗粒度的并行，并且在parallel的末尾有一个隐含的同步屏障，所有线程完成所需的重复任务后，将各个同步屏障汇合，然后可以从各个线程收集所需要的数据合成所需要结果。

利用parallel for 并行原理是采用工作分配的执行方式，将循环所需要工作量按一定方式分配到各个执行线程，所有线程执行工作总和是原串行完成工作量。此方式对一个确定并且完整的for循环进行分割，分割成多段在不同CPU上运行。

4.2按行划分矩阵向量相乘

程序要点：

利用parallel指令的复制执行的方式，利用各个线程的ID号划分了工作任务，将矩阵按行划分分配给各个线程，通过获取线程号来分布不同任务。

实现按行划分的矩阵向量乘法的程序关键代码如下：

4.3按列划分的算法实现

程序要点：

利用parallel指令的复制执行的方式，利用各个线程的ID号划分了工作任务，将矩阵按列划分分配给各个线程，通过获取线程号来分布不同任务。

实现按列划分的矩阵向量乘法的程序关键代码如下：

五、算法实现

5.1最终计算结果

进行上机实验，开发环境为Microsoft Visual Studio 2010（旗舰版）

表一　4个进程计算结果（OpenMP）

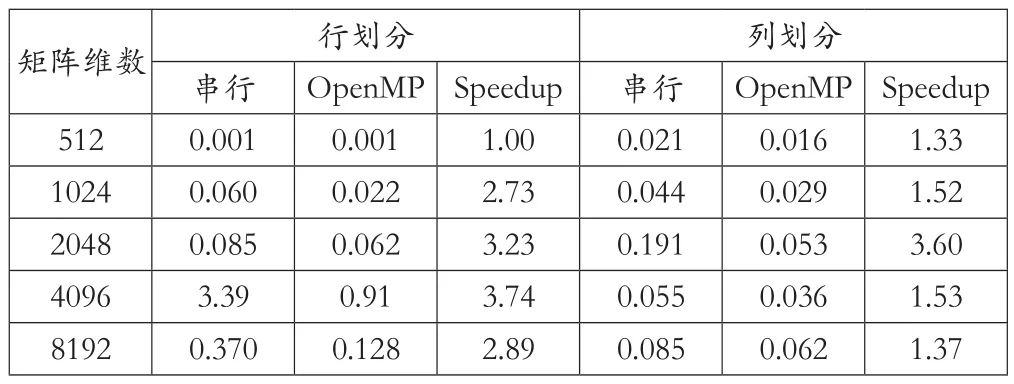
表二　8个进程计算结果（OpenMP）

六、数值实验和结论

6.1图表分析

图一　4个进程计算结果加速比增长关系（openMP）

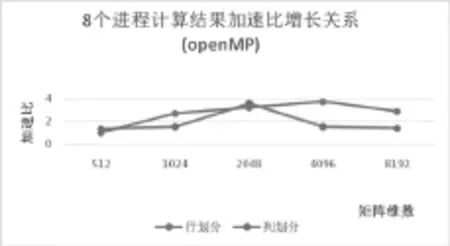
图二　8个进程计算结果加速比增长关系（openMP）

6.2实验结论

通过对上述图表分析，我们可得到以下结论：

（1）OpenMP中随着维数的增长，行划分和列划分方式加速比逐渐增长，但所用的进程数目较大时，加速比和效率较为明显，因为线程数目越大，每个线程分配的任务量相对越小，运行效率越快。

（2）随着维数的增高，按行划分是相对有效的方法。按列划分在分发时需要分发的次数为维数的倍数，分发的时间将大大增加。按列划分需要将矩阵进行块划分。然后再进行分发，相对来讲，增大了时间的消耗。

（3）在工程计算中，当矩阵维数较大时，可以采取按行划分的方式大大增加计算速度，而当矩阵维数较小时，建议使用串行算法。

［1］ 朱建伟.多线程并行快速求解e值的六种方法［J］.现代计算机：普及版.2013（17）.15-20

［2］多核系列教材编写组.多核程序设计［M］.北京.清华大学出版社，2007

［3］ 邓倩妮.并行程序设计导论［M］.北京.北京机械工业出版社.2012.8

［4］尚智，陈硕.大型矩阵相乘并行计算的特性分析［J］.Software Engineering，2013.02（1）：15-19

郝静（1994—），女，汉族，山东烟台人，中国石油大学（华东）理学院，2013级本科生，数学与应用数学专业

刘雅坤（1995—），女，汉族，山东青岛人，中国石油大学（华东）理学院，2013级本科生，数学与应用数学专业