一类具阻尼项和多滞量的广义Emden-Fowler中立型微分方程的振动性

林 文 贤

(韩山师范学院数学与统计学院，广东 潮州 521041)



一类具阻尼项和多滞量的广义Emden-Fowler中立型微分方程的振动性

林 文 贤

(韩山师范学院数学与统计学院，广东 潮州 521041)

通过利用Riccati变换和Young不等式，获得了具阻尼项和多滞量的广义Emden-Fowler中立型泛函微分方程的振动准则，推广和改进了最近文献的结果.

广义Emden-Fowler型微分方程；振动准则；阻尼项

1　预备知识

在核能物理、化学反应系统、气体动力学、流体力学等方面有着众多应用的Emden-Fowler方程x″(t)+λ(t)|x(t)|α-1x(t)=0(α>1)是一个半线性微分方程，基于其广泛的实际应用背景，吸引了很多学者的研究兴趣.[1-8]本文将讨论一类具阻尼项和多滞量的广义Emden-Fowler中立型泛函微分方程

(1)

其中y(t)=x(t)+p(t)x(τ(t))，φ(s)=|s|α-1s，α是常数，n(≥2)是一个偶数.假设下列条件成立：

(H1)p(t)，q1(t)，q2(t)∈C(I，[0，∞))，I=[t0，∞)，0≤p(t)≤p<1；

(H2)βn>βn-2>…>β2>α>βn-1>βn-3>…>β1>0均为常数；

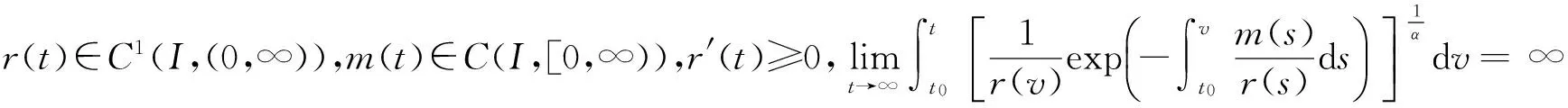
当m(t)=0，n=2时，方程(1)就是文献[6]所研究的方程.本文的目的是建立方程(1)的若干振动准则，从而文献[6]结论为本文结果的特例，并推广了文献[7-8]的相应结果.关于本文中的函数不等式，如果没有特别说明，都是对一切充分大的t成立.

2　主要结果

引理1设x(t)是方程(1)的最终正解，则存在t1≥t0，使得y(t)>0，y′(t)>0，y″(t)≤0，t≥t1.

证明设x(t)是方程(1)的最终正解，由条件(H1)和(H4)，

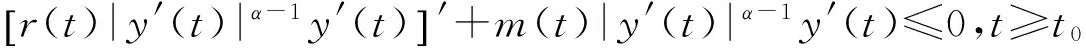
下证y′(t)>0. 事实上，若存在t1≥t0，使y′(t1)<0，注意到

是t的减函数，有

从t1到t积分得

注意到r′(t)>0，可得y″(t)≤0，t≥t1.

引理2设x(t)是方程(1)的最终正解，且存在某个i0∈{1，2，…，n}，使得

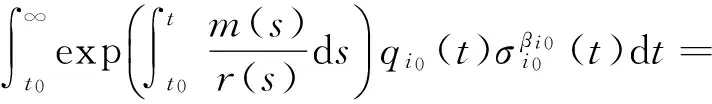
(2)

证明设x(t)是方程(1)的最终正解，由引理1知y′(t)>0， 从而x(t)>(1-p)y(t). 再由方程(1)得

(3)

定义函数φ(t)=y(t)-ty′(t)，则φ′(t)=-ty″(t)>0，故φ(t)单调增加且最终定号.

(4)

联合(3)—(4)式，

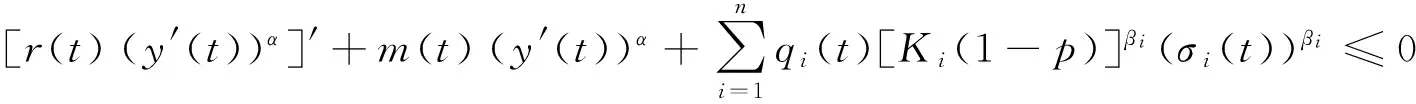
即

对上式积分，有

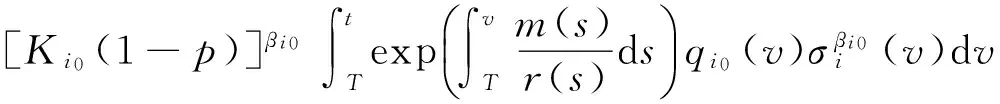
上式中令t→∞，这与(2)式矛盾，因此φ(t)>0成立.

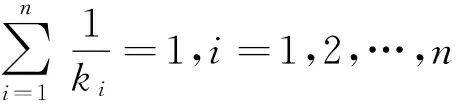
证明设f(x)=lnx，因f″(x)<0，故f(x)是当x>0时的严格凹函数，所以

定理1设存在某个i0∈{1，2，…，n}，使得(2)式成立，且存在函数ρ(t)∈C1(I，(0，∞))，使得

(5)

其中

(6)

(7)

则方程(1)是振动的.

证明设x(t)是方程(1)的非振动解，不失一般性，可设x(t)>0，t≥t0.由引理1，y(t)>0，y′(t)>0，t≥t1.令

(8)

则

利用(3)和(8)式，

(9)

由引理3，可得

其中σ(t)≤min{σ1(t)，σ2(t)，…，σn(t)}，ki(i=1，2，…n)由(7)所定义.

因此(9)式化为

(10)

(11)

联合(7)，(10)—(11)式，

(12)

再由引理4，

(13)

对上式积分得

令t→∞，注意到(5)式，有W(t)→-∞，这与W(t)>0矛盾. 因此方程(1)没有最终正解，故方程(1)振动.

推论1设存在某个i0∈{1，2，…，n}，使得(2)式成立，且

(14)

则方程(1)是振动的.

证明只需在定理1中取ρ(t)=1即可.

下面给出方程(1)的Kamenev型振动准则.

定理2设除(5)式外定理1的全部假设都成立.若当n>1时，

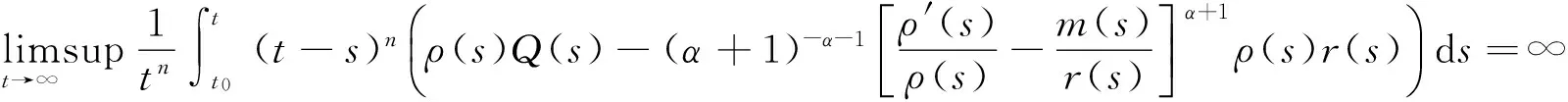
(15)

其中Q(t)由(7)式定义，则方程(1)是振动的.

证明如同定理1的证明，设x(t)是方程(1)的非振动解，不失一般性，设x(t)>0，x(τ(t))>0，x(σ1(t))>0，x(σ2(t))>0，t≥t1，故有y(t)>0. 令W(t)的定义同(8)式，则W(t)>0，t≥t1，且(13)式成立，从而

注意到

有

因此

上式与条件(15)矛盾. 定理2证毕.

下面利用Philos型的积分平均技巧[10]，得出方程(1)新的振动定理.为此引进如下一类函数C. 令D={(t，s)|t≥s≥t0}，D0={(t，s)|t>s≥t0}.函数H(t，s)∈C(D，R)称为属于C类，记作H∈C，如果：

(ⅰ)H(t，t)=0，t≥t0;H(t，s)>0，(t，s)∈D0.

(16)

定理3设存在某个i0∈{1，2，…，n}，使得(2)式成立，且存在函数ρ(t)∈C1(I，(0，∞))和H∈C，使得

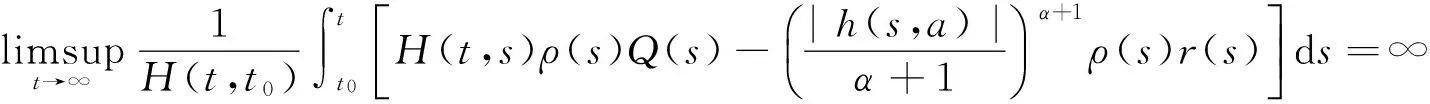
(17)

其中h(t，s)由(16)式定义.则方程(1)是振动的.

证明设x(t)是方程(1)的非振动解，不妨设x(t)>0，x(τ(t))>0，x(σ1(t))>0，x(σ2(t))>0，t≥t1，故有y(t)>0. 令W(t)的定义同(8)式，则W(t)>0，t≥t1，且(12)式成立. 记

则由(12)式得到

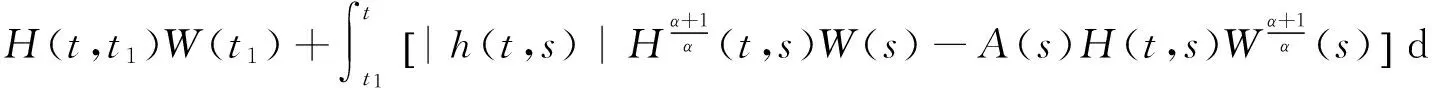
对上式利用引理4且注意到A(s)的定义，有

因此

上式与条件(17)矛盾. 定理3证毕.

[1]ELBERT A. A half-linear second order differential equation[J]. Acta Mathematica Hungarica，1987，49:487-508.

[2]HORNG JAAN LI，CHEH CHIH YEH. Oscillations of half-linear second order differential equations[J]. Hiroshina Math J，1995，25：585-594.

[3]RAVI P，GRACE R P，AGARWAL S R. On the oscillation of certain second order differential equations[J]. Georgian Mathematical Journal，2000，7(2)：201-213.

[4]朱刚，任洪善，俞元洪.具有连续分布时滞的非线性中立型双曲微分方程解的振动性[J]. 东北师大学报(自然科学版)，2007，39(2):6-10.

[5]林文贤. 具有阻尼项的中立型Emden-Fowler方程的区间振动准则[J].韩山师范学院学报，2011，32(6)：8-11.

[6]林丹玲. 半线性中立型二阶时滞微分方程的振动准则[J].安徽大学学报，2015，39(1)：15-20.

[7]ERBE L，HASSAN T S，PETERSON A. Oscillation of second order neutral delay differential equations[J]. Adv Dynamical Systems Appl，2008，3(1)：53-71.

[8]LIU H，MENG F，LIU P. Oscillation and asymptotic analysis on a new generalized Emden-Fowler equations[J].Appl Math Comput，2012，219(5):2739-2748.

[9]HARDY G H，LITTERWOOD J E，POLYA G.Inequalities[M]. Cambridge：Cambridge University Press，1952：66.

[10]PHILOS CH G. Oscillation theorems for linear differential equation of second order[J]. Arch Math，1989，53(3)：483-492.

(责任编辑：李亚军)

Oscillation for generalized Emden-Fowler neutral functional differential equations with damping terms and multiple delays

LIN Wen-xian

(College of Mathematics and Statistics，Hanshan Normal University，Chaozhou 521041，China)

By using Riccati transformation method and Young’s inequality，some new interval oscillatory criterion for generalized Emden-Fowler neutral functional differential equations with damping terms and multiple de1ays are obtained. The results generalize and improve some known results.

generalized Emden-Fowler functional differential equations；oscillation criteria；damping terms

1000-1832(2016)03-0025-05

2015-04-10

广东省自然科学基金资助项目(S2013010013372)；广东省高等教育教学改革项目(GDJG20142396)；广东省高等学校特色创新项目(2014GXJK125).

林文贤(1966—)，男，教授，主要从事泛函微分方程理论及其应用研究.

O 175.13[学科代码]110·51

A

[DOI]10.16163/j.cnki.22-1123/n.2016.03.006