测试三轴转台误差分析及建模

李慧鹏，曹亚运，高　爽，季伟峰

（1.北京航空航天大学惯性技术重点实验室，北京100191；2.中国地质科学院探矿工艺研究所，成都611734）

测试三轴转台误差分析及建模

李慧鹏1，曹亚运1，高爽1，季伟峰2

（1.北京航空航天大学惯性技术重点实验室，北京100191；2.中国地质科学院探矿工艺研究所，成都611734）

以用于测斜仪的三轴转台为研究背景，通过分析其运动规律，探讨了三轴转台不正交度误差源对三轴转台精度的影响，并用MATLAB对它进行了误差建模，仿真计算得出了系统装配不正交时三个坐标的误差率；最后，引入实际测试过程中角度传感器的测量误差，在三轴不正交的前提下又对三坐标测量误差进行了数学建模，通过仿真分析，研究探讨了角度传感器带来的误差规律，在实际应用中为测斜仪标定测试和误差补偿提供了理论依据。

三轴转台；误差建模；误差仿真；转移矩阵

0　引言

转台作为一种测试、半实物仿真的核心设备，其性能直接影响实验的精度。在实际操作中，由于转台设备在制造中热变形、摩擦、振动以及安装过程中误差因素的影响，使得转台在实际运动过程中的轨迹与理想运动轨迹不完全重合，存在一定的误差，最终导致整个系统的精度受到影响。因此，深入研究转台转动时的各个误差来源，并对其进行误差分析建模，采取相应措施消除各类误差因素，对提高整个系统的仿真、测试精度具有不可或缺的意义。本文研究的对象是用于测斜仪标定的三轴转台，研究的主要误差来源是三轴转台的不正交度。根据系统运动理论，分析了不正交度误差源对转台设备系统的影响，对三个坐标轴的误差率进行了误差建模，从而为测斜仪标定过程中的误差分配和误差补偿提供理论依据。

1　理想情况下的状态转移矩阵

测斜仪在实际工作过程中，可以看作刚体在空间三维坐标系中的运动，因此测斜仪的工作状态特性可以由三轴转台来模拟。图1是三轴转台的结构示意图，三个轴分别是方位轴、俯仰轴和横滚轴。图2是三轴转台的坐标变换关系示意图，OX0Y0Z0表示地理坐标系，即初始位置的正交坐标系，作为被测件的参考坐标系。OX1Y1Z1表示方位框架坐标系，OX2Y2Z2表示横滚框架坐标系，OX3Y3Z3表示俯仰框架坐标系；从三个轴处于正交时开始，方位轴绕其转动轴OX0逆时针转动一个角度α，横滚轴绕其转动轴OY1逆时针转动一个角度β，俯仰轴绕其转动轴OZ2逆时针转动一个角度γ，得到转动后的坐标关系如图2所示。

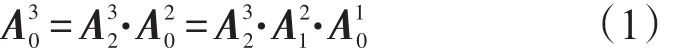
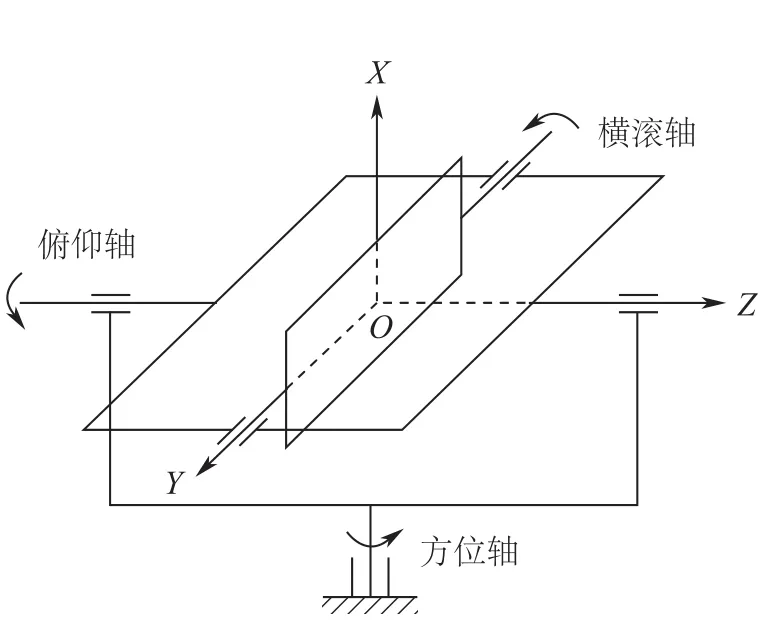
图1　三轴转台结构示意图Fig.1　Scheme of the three-axis

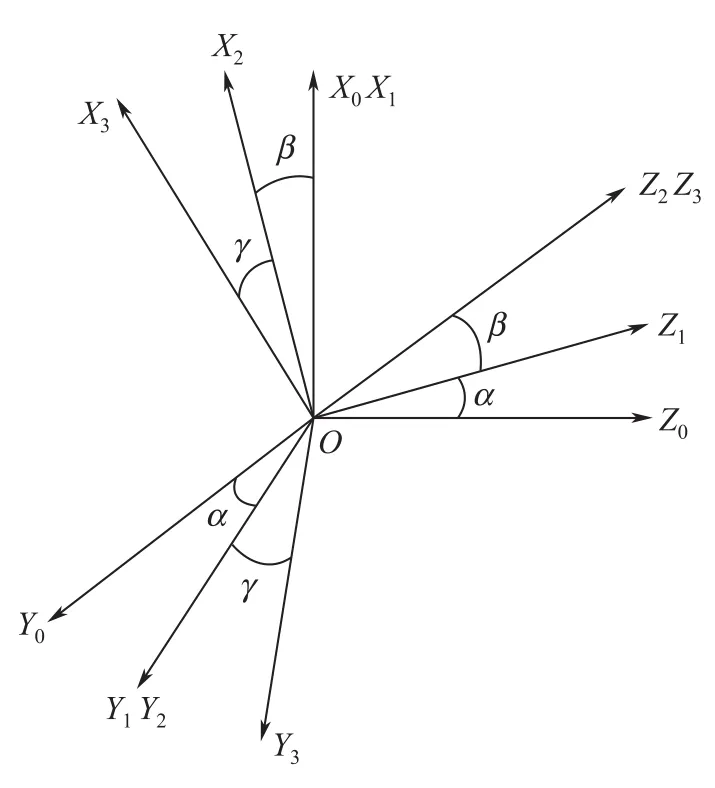
图2　三轴转台坐标变换关系示意图Fig.2　Scheme of three coordinates’changes

设（x0，y0，z0）为初始坐标，（x3，y3，z3）为旋转后的坐标，则两坐标关系如式（3）所示。

2　误差建模

2.1初始实际坐标值计算

定义OXaYaZa为实际旋转时的直角坐标系，OXiYiZi为理想直角坐标系。

在实际坐标系和理想坐标系不完全重合的前提下，设Xa投影在Xi-Yi平面内与Yi正半轴之间的误差夹角为δΔxy；Xa投影在Xi-Zi平面内与Zi正半轴之间的误差夹角为δΔxz。同理，可定义δΔyx、δΔyz、δΔzx、δΔzy，则可以求出Xi与Xa，Yi与Ya，Zi与Za的误差夹角为δx、δy、δz。

假设在三轴不正交的情况下测得一个点的坐标为（i，j，k）a，根据以上推算，可以推出该点在理想直角坐标系下的坐标为（i，j，k）i，其关系如式（5）所示。

2.2状态转移矩阵矫正

已知在三维空间直角坐标系中，空间中任意一点绕过原点的直线向量（x，y，z）按照右手定则旋转一定角度后，得到的状态转移矩阵为式（6）。这里规定坐标系是右手系，矢量（x，y，z）必须是单位化了的经过坐标原点的直线向量。

由前面推算可知，实际的Xa在理想直角坐标系下的单位直线向量为（1，tanδΔxy，tanδΔxz）/Mx；Ya在理想直角坐标系下的单位直线向量为（tanδΔyx，1，tanδΔyz）/My；Za在理想直角坐标系下的单位直线向量为 （tanδΔzx，δΔzy，1）/Mz，所以，当物体绕X轴旋转时理想状态转移矩阵为Tαi，如式（7）所示。同理可以得到当沿Y轴Z轴旋转β、γ时的理想状态转移矩阵Tβi、Tγi。

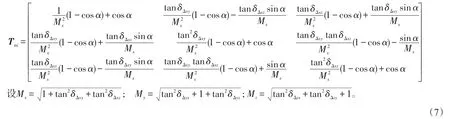
因为误差角很小所以，δmn→0，所以tanδmn→δmn。（m，n为任意x，y，z两两组合），所以可以化简转移矩阵为Tαa、Tβa、Tγa，如式（8）～式（10）所示。

综上所述，当一个在初始不正交坐标系下空间坐标点为（i，j，k），经过初始矫正，绕OXaYaZa分别按照右手定则旋转α、β、γ后，两坐标关系如式（11）所示。

3　误差仿真

用MATLAB对三个坐标的误差率进行仿真分析。如图3～图5所示，根据式（2）和式（11）对三个坐标的误差进行误差建模，分析在三轴转动的角度一定的情况下，当误差角度变化时对三个坐标误差率影响，以及当误差角度一定时，转动度数变化对三个坐标误差率的影响；可以看出当误差角存在时，三个坐标存在一定的误差率，误差率的范围大约在10-3数量级。

图3　坐标误差率跟随δΔxy、δΔxz变化的误差曲线图Fig.3　Error curve chart of coordinate error rate with δΔxy、δΔxzchanges

图3是当α=β=γ=45°，且δΔyz=δΔyx=δΔzx=δΔzy=0时，三个坐标误差率跟随δΔxy、δΔxz变化的误差曲线图。

图4　坐标误差率跟随δΔxy变化的误差曲线图Fig.4　Error curve chart of coordinate error rate with δΔxychanges

图5　坐标误差率跟随β、γ变化的误差曲线图Fig.5　Error curve chart of coordinate error rate with β、γ changes

图4是当α=β=γ=45°，δΔxz=δΔyz=δΔyx=δΔzx=δΔzy=0.01°时，三个坐标误差率跟随δΔxy变化的误差曲线图。

图5是当δΔxy=δΔxz=δΔyz=δΔyx=δΔzx=δΔzy=0.01°，α= 45°时，三个坐标误差率跟随β、γ变化的误差曲线图。

在实际转动过程中，编码器存在测量误差，假设已知外框编码器测量误差Δα=0.01°sin（α），中框编码器测量误差Δγ=0.01°sin（γ），内框编码器测量误差Δβ=0.01°sin（β）。图6是当α=60°，β= 60°，γ变化时三个坐标的误差率曲线图（假设δΔxy= δΔxz=δΔyz=δΔyx=δΔzx=δΔzy=0.01°）。图7是当α=60°，β=60°，γ变化时，由于编码器存在而带来的三个坐标误差的相对变化率（假设δΔxy=δΔxz=δΔyz=δΔyx=δΔzx=δΔzy= 0.01°），从图7中可以看出误差曲线成正弦函数变化。

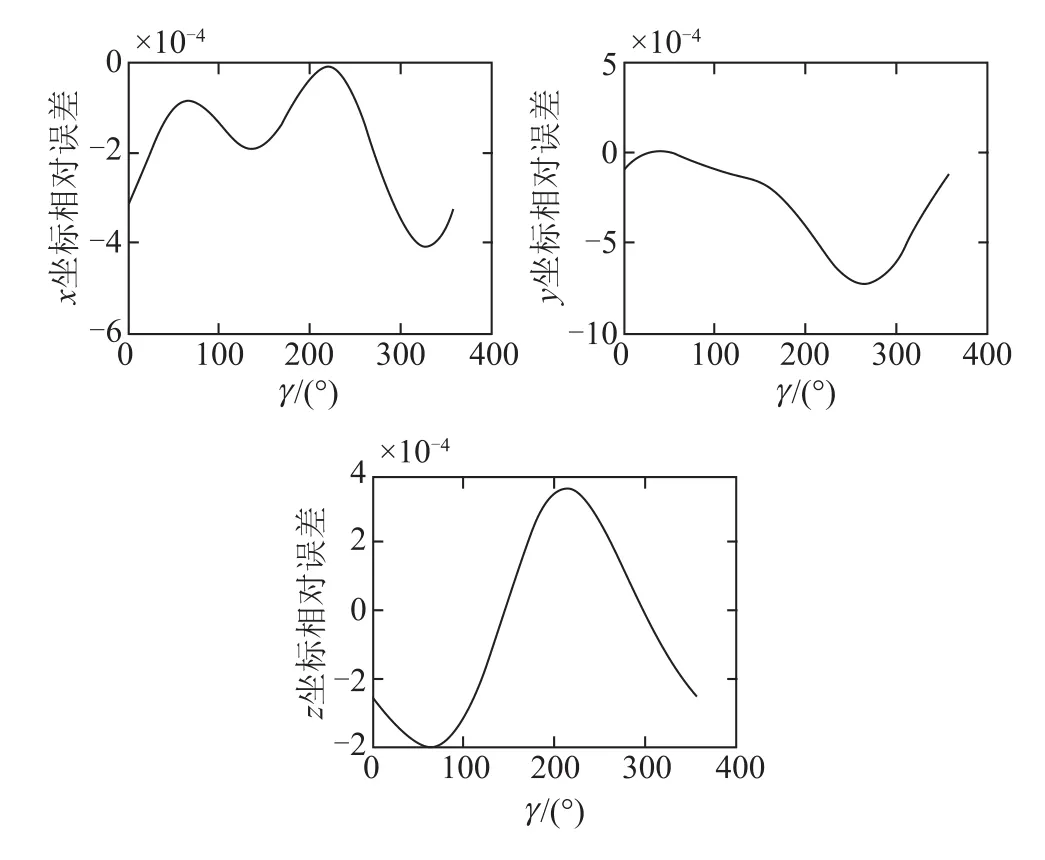
图7　γ角度变化时，三个坐标的相对误差Fig.7　Coordinates’absolute error when γ changes

4　结论

本文通过对用于测斜仪标定的三轴转台的安装不正交度误差以及角度传感器测量误差进行分析，对其进行误差建模，仿真计算出了三个坐标误差率随三轴转台的转动角度的曲线变化规律。这为测斜仪的标定和测试提供了理论依据，在测斜仪实际测试标定中对误差来源分配和误差补偿具有重要的实践指导意义。

［1］Y Lin，Y Shen.Modeling of five-axis machine tool metrology models using the matrix summation approach［J］.Advanced Manufacturing Technology，2003，21（4）∶243-248.

［2］V.S.B.Kiridena，P.M.Ferreira.Kinematic modeling of quasistatic errors of three-axis machining centers［J］.International Journal of Machine Tools&Manufacture，1994，34（1）∶85-100.

［3］ 夏斯.三轴测试转台精度特性分析和控制系统设计［D］.哈尔滨工业大学，2010. XIA Si.Three accuracy properties of three-axis test table and control design［D］.Harbin Institute of Technology，2010.

［4］曲志勇，姚郁.仿真转台误差分析及误差建模［J］.计算机仿真，2006，23（3）∶301-304. QU Zhi-yong，YAO Yu.Error analysis and error modeling of simulation turntable［J］.Computer Simulation，2006，23（3）∶301-304.

［5］ Louis A，De More.Design study for a high-accuracy three-axis test table［J］.AIAA Guidance and Control Conference，1985，10（1）∶104-114.

［6］李凡，朱国力.三轴标定转台的指向误差建模与仿真分析［J］.机械工程与自动化，2014，187（6）∶147-149. LI Fan，ZHU Guo-li.Modeling and simulation analysis of pointing error for three-axis calibration rotary table ［J］.Mechanical Engineering and Automation，2014，187 （6）∶147-149.

［7］赵玉华，袁峰，丁振良.三轴仿真转台误差建模与分析

［J］.四川大学学报，2010，42（6）∶228-229. ZHAO Yu-hua，YUAN Feng，DING Zhen-liang.Error modeling and analysis of three-axis simulation turntable［J］.Journal of Sichuan University，2010，42（6）∶228-229.

［8］白雪峰，赵剡.单轴速率三轴位置惯性测试转台误差及传递分析［J］.航天控制，2006，24（2）∶26-29. BAI Xue-feng，ZHAO Yan，Errors propagation analysis of single-axis rate and three-axis position turntable［J］. Aerospace Control，2006，24（2）∶26-29.

［9］ Zhiyong QU，Yu Yao.Derivation of error models and error compensation procedure for simulation turntable using multi-body kinematics［C］.International Conference on Mechatronics&Automation Niagara Falls，2005∶1408-1411.

［10］ Z.S.Wang，Y.Wang，B.K.Su.Friction compensation for high precision turntable using adaptive sliding mode controller［J］.Industrial Electronics and Applications，2007∶1090-1094.

ErrorAnalysis and Modeling of Test Three-axis Turntable

LI Hui-peng1，CAO Ya-yun1，GAO Shuang1，JI Wei-feng2
（1.Key Laboratory on Inertial Science and Technology，Beihang University，Beijing 100191；2.Institute of Exploration Technology，Chengdu 611734）

Through analyzing the inclinometer’s three-axis turntable motion principle，this paper discusses the influence on the accuracy of three-axis turntable which is generated by the error source of three-axis nonorthogonality.And we build systematic error modeling as well as obtain three coordination’s error rate by simulating calculation.At last，by introducing actual angular transducer measuring error，we achieve a mathematical modeling on the premise of three-axis nonorthogonality.The research studies the angular transducer error pattern by simulation analysis，thus it provides theoretical foundation for inclinometer test and error compensation.

three-axis turntable；error modeling；error simulation；transfer matrix

TP202

A

1674-5558（2016）05-01110

10.3969/j.issn.1674-5558.2016.02.016

2015-04-20

李慧鹏，男，副教授，研究方向为惯性技术与组合导航。