植物空间分布格局中邻体距离的概率分布模型及参数估计

高　猛

中国科学院烟台海岸带研究所，海岸带环境过程与生态修复重点实验室，烟台　264003



植物空间分布格局中邻体距离的概率分布模型及参数估计

高猛*

中国科学院烟台海岸带研究所，海岸带环境过程与生态修复重点实验室，烟台264003

最近邻体法是一类有效的植物空间分布格局分析方法，邻体距离的概率分布模型用于描述邻体距离的统计特征，属于常用的最近邻体法之一。然而，聚集分布格局中邻体距离(个体到个体)的概率分布模型表达式复杂，参数估计的计算量大。根据该模型期望和方差的特性，提出了一种简化的参数估计方法，并利用遗传算法来实现参数优化，结果表明遗传算法可以有效地估计的该模型的两个参数。同时，利用该模型拟合了加拿大南温哥华岛3个寒温带树种的空间分布数据，结果显示：该概率分布模型可以很好地拟合美国花旗松(P.menziesii)和西部铁杉(T.heterophylla)的邻体距离分布，但由于西北红柏(T.plicata)存在高度聚集的团簇分布，拟合结果不理想；美国花旗松在样地中近似随机分布，空间聚集参数对空间尺度的依赖性不强，但西北红柏和西部铁杉空间聚集参数具有尺度依赖性，随邻体距离阶数增加而变大。最后，讨论了该模型以及参数估计方法的优势和限制。

空间点格局；聚集分布；参数优化；遗传算法

植物种群空间分布格局是指特定时间内, 植物群落中某一种群的个体在空间的分布状况[1-3]。空间分布格局分析对于确定种群特征、种群间相互关系以及种群与环境之间的关系具有非常重要的作用, 对于了解种群空间分布规律以及种内与种间关系具有重要的意义[4-7]。按照种群内个体的聚集程度和方式, 种群分布格局一般可分为随机分布、均匀分布和聚集分布3种类型[8]。以频度/密度为基础的样方法和以距离为基础的无样地法属于两大类确定植物空间分布格局的研究方法[3-5，9]。植物群落调查实践表明无样地法比于样方法在成本和可操作性两方面均有一定的优势[10]。

最近邻体法(nearest neighbor method, NN)属于无样地法之一，它最早由Clark 和Evans[11]提出，以观测点与个体之间的距离(或者个体与个体之间的距离)为原始数据获取分析指标，用统计检验的方法考察实际值与理论期望值之间的差异显著性，进而判断种群的空间分布类型。Stoyan和Penttinen[12]指出最近邻体距离特别是高阶邻体距离的概率分布比一般的分析指标可以更好地量化空间分布格局。Thompson[13]早在1956年便推导出了随机分布格局中邻体距离的概率分布模型，Eberhardt[14]则给出了聚集分布格局中随机观测点到相邻个体距离的概率分布模型，Magnussen[15-16]等基于Eberhardt的概率分布模型提出了植物空间密度的点估计方法。在随机分布格局中，任意选择的观测点到其相邻个体距离与任意选择的个体到其相邻个体距离在统计学意义上是一致的，因此二者的概率分布模型也是一样的[6]。聚集分布格局中，任意选择的观测点到相邻个体距离和个体到个体距离并不一致，二者的概率分布模型也不相同。Gao[5]利用条件概率的极限法推导出聚集分布格局下的个体到相邻个体的概率分布模型，并以巴拿马Barro Colorado岛(Barro Colorado Island, BCI)样地183个热带雨林树种的空间分布数据进行了验证，结果表明该概率分布模型可以较好地拟合大多数树种的邻体距离分布。Gao[6]等利用该模型研究了BCI样地中树种分布多尺度特征，并总结出5类空间聚集指数-邻体距离阶数曲线。BCI样地属于热带雨林，物种丰富且大多数树种被证实在空间中聚集分布[17]，这与Gao[5]模型的基本条件一致。本文的第一个研究目标是利用Gao[5]的邻体距离概率分布模型拟合加拿大西海岸南温哥华岛3个寒温带树种的空间分布数据，以检验该模型在北方森林的适用性。

Eberhardt概率分布模型含两个参数，概率密度函数的表达式较复杂。Magnussen[15-16]等在利用Eberhardt模型进行密度估计时采用了极大似然法(maximum likelihood)，参数优化则基于Nealder-Mead算法。Gao模型与Eberhardt模型的概率密度函数的表达式相似，并通过求解极大似然数值方程来完成参数估计[5-6]。以上两种参数估计方法均属于极大似然法的范畴，当模型样本较少时，其求解过程可能只得到局部最优解而非全局最优解[16]。遗传算法(genetic algorithm)是一种通过模拟自然进化过程搜索最优解的方法，其主要特点是：直接对结构对象进行操作，不存在求导和函数连续性的限定，具有更好的全局寻优能力；采用概率化的寻优方法，能自动获取和指导优化的搜索空间，自适应地调整搜索方向，不需要确定的规则。遗传算法的这些性质，使其成为现代智能计算中的关键技术。本文的第二个研究目标是采用遗传算法估计Gao模型的两个参数，解决极大似然法数值优化不能得到全局最优解的问题。

1　模型

植物空间分布格局分析中，将个体的空间位置映射到二维空间上的点，形成空间点格局。空间点格局在统计学中被认为是空间点过程的一个实现[18]。空间点过程最基本的属性是过程强度λ(s)，即位置s单位面积内的期望点数。随机分布的空间点格局，λ(s)为常量，对应一个Poisson过程。定义随机采样点到其第n个相邻个体的距离为随机变量rn，其概率分布模型的密度函数为[13]：

(1)

式中,n记为邻体距离的阶数。如果假设λ(s)服从均值为λ的Gamma分布h(λ|α,β)，则面积A的样地内点的个数服从期望为λA的负二项分布[19]。负二项分布是聚集分布格局分析中最普遍的概率分布模型[4]。将Gamma分布h(λ|α,β)带入模型(1)，通过计算卷积可以得到聚集空间分布格局中rn的概率密度函数[15]:

(2)

式中,α>0，β>0，且满足λ=α×β，Γ()为Gamma函数。需要估计的两个模型参数为α和β。定义任意个体到其第n个相邻个体的距离定义为随机变量sn，聚集分布点格局中，sn的概率密度函数为[5]：

(3)

模型(3)与模型(2)的表达式相似，利用邻体距离的样本数据可以估计α和β的值。

2　数据与方法

2.1数据

本文以加拿大西海岸3个寒温带树种的空间分布数据验证概率分布模型(3)。研究区位于不列颠哥伦比亚省的南温哥华岛(48°38′ N,123°43′W)，样地大小为102m×87m(0.8874hm2)，平均海拔382m[20](图1)。3个树种分别为西部红柏(Western red cedar,Thujaplicata)，美国花旗松(Douglas-fir,Pseudotsugamenziesii)，以及西部铁杉(Western hemlock,Tsugaheterophylla)。在统计个体到个体的邻体距离时，为避免边缘效应，在样地边界设置5m的缓冲区，即靠近样地边界5m内的个体不作统计，共计西部红柏337棵，美国花旗松508棵，西部铁杉767棵。

图1　3个树种的空间分布点格局Fig.1　Spatial distribution point patterns of three tree species

2.2遗传算法

遗传算法是人工智能领域中用于解决最优化的一种启发式算法，这种算法借鉴了进化生物学中的一些现象，包括遗传、突变、自然选择以及杂交等[21]。图2展示了8位编码的遗传算法计算流程图。选取适当的目标函数，便可以利用遗传算法估计模型(3)的参数。本研究中遗传算法是在数学软件MATLAB2008[22]环境下实现的，并编写遗传、突变、自然选择以及杂交4个计算过程的通用函数。

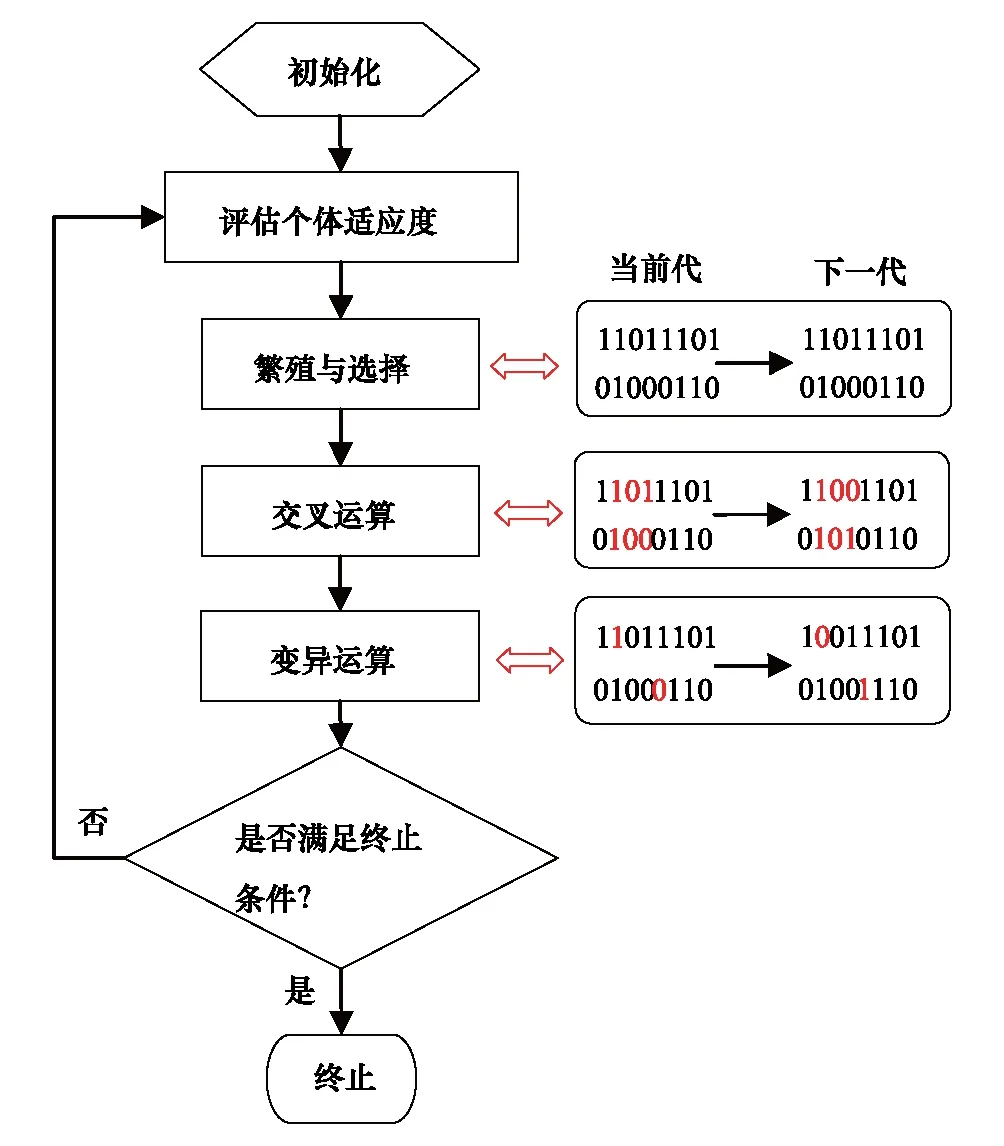
图2　遗传算法的计算流程图Fig.2　Computation flowchart of Genetic Algorithm

2.3参数估计

根据模型(3)概率密度的表达式，可以分别计算随机变量sn的期望和方差：

(4)

(5)

(6)

为验证参数估计结果，概率分布模型(3)的拟合优度采用Kolmogorov-Smirnov(KS)检验，检验统计量KS定义为：

(7)

式中,T(sn)和O(sn)分别为n阶邻体距离不大于sn的拟合及实际概率。

3　结果

表1　西部红柏(T. plicata)的邻体距离概率分布模型的参数估计和检验结果

图3　西部红柏(T. plicata)的邻体距离概率密度函数(左侧纵坐标)及概率分布函数(右侧纵坐标)Fig.3 　Probability density (left y-axis) /distribution functions (right y-axis) of nearest neighbor distance of Western red cedar (T. plicata)

表2　美国花旗松(P. menziesii)的邻体距离概率分布模型的参数估计和检验结果

图4　美国花旗松(P. menziesii)的邻体距离概率密度函数(左侧纵坐标)及概率分布函数(右侧纵坐标)Fig.4 　Probability density (left y-axis)/distribution functions (right y-axis) of nearest neighbor distance of Douglas-fir (P. menziesii)

表3　西部铁杉(T. heterophylla)的邻体距离概率分布模型的参数估计和检验结果

图5　西部铁杉(T. heterophylla)的邻体距离概率密度函数(左侧纵坐标)及概率分布函数(右侧纵坐标)Fig.5　Probability density (left y-axis) /distribution functions (right y-axis) of nearest neighbor distance of Western hemlock (T. heterophylla)

4　结论与讨论

本文根据聚集分布格局中邻体距离(个体到个体)的概率分布模型期望和方差的特性，提出了一种简化的参数估计方法，利用遗传算法实现参数优化，并以加拿大南温哥华岛3个寒温带树种的空间分布数据进行了实例验证，得到的主要结论如下：

(1)通过定义合适的目标函数，可以简化模型参数估计的计算量，遗传算法可以有效地估计邻体距离概率模型的参数；

(2)西部红柏(T.plicata)和西部铁杉(T.heterophylla)的空间聚集度比较高，美国花旗松(P.menziesii)在样地中近似随机分布，Gao[5]的邻体距离概率分布模型可以很好地拟合西部铁杉(T.heterophylla)和美国花旗松(P.menziesii)的邻体距离概率分布。

邻体距离概率分布模型(3)的表达式较为复杂，Gao[5]在利用极大似然估计的方法估计模型参数时，定义了一个带有绝对值的目标函数。因此，参数估计问题转化为二维参数空间上的数值最优化问题。在计算过程中，样本的选择会影响数值优化算法的结果，特别是当邻体距离的样本较少时，会得到局部最优解而非全局最优解。本文提出利用遗传算法估计模型(3)的参数α和β，在定义目标函数(6)之后将参数估计问题转化为一维参数空间上的数值最优化问题。遗传算法在的作用是作为一种数值最优化技术解决一维参数空间上的数值最优化问题。然而，该方法仍然不能有效解决当样本少的时候估计不准确的问题。首先，本文提出的参数方法实质上是一种矩估计方法。矩法估计方法的优点是原理简单、使用方便，使用时可以不知总体的分布。理论上讲，矩法估计是以大样本为应用对象的，只有在样本容量较大时，才能保障它的优良性。因此，准确估计参数的关键是获得足够的邻体距离样本，这对两种估计方法都很重要。遗传算法本身对参数估计的精度不具有决定性作用。

邻体距离概率分布模型(3)是从聚集空间点格局的负二项分布模型推导而来的，参数α与负二项分布模型中的聚集指数k等价，其本身就与空间尺度相关[23-24]。植物空间分布格局分析中空间尺度概念涉及3个方面：研究区域的尺度、生态过程尺度和取样尺度[2,25]。利用邻体距离分析空间分布格局也受到尺度的影响，在实际应用中需要关注取样尺度，即邻体距离的阶数。选取比较小的阶数会忽略掉较多的空间信息，选取较大的阶数会增加群落调查的工作量，并且还会受到边际效应的影响[5]，所以建议采用的阶数是2到6。然而，模型(3)本身也有一定的局限性，因此在拟合聚集度较高的空间点格局的邻体距离时的，拟合效果并不理想[5-6]，以及本文中的西部红柏的邻体距离分布。拟合效果不理想的原因有两个：1)实际的概率分布会出现多峰值的现象；2)实际概率向左倾斜的较多。针对以上两个问题，可以从以下2个方面进行改进：1)改进概率分布模型，例如采用混合型概率分布；2)采用高阶的邻体距离，使得概率分布右移。下一步的研究可以尝试采用人工智能方法对极大似然估计的目标函数进行优化，可以避免在样本较少的情况下不能得到全局最优解。

[1]Gaston Kevin J. Rarity. London: Chapman and Hall, 1994.

[2]Fortin Marie Josee, Dale Mark R T. Spatial analysis: a guide for ecologists. Cambridge: Cambridge University Press, 2005.

[3]王本洋, 余世孝. 种群分布格局的多尺度分析. 植物生态学报, 2005, 29(2): 235-241.

[4]兰国玉, 雷瑞德. 植物种群空间分布格局研究方法概述. 西北林学院学报, 2003, 18(2): 17-21.

[5]Gao M. Detecting spatial aggregation from distance sampling: a probability distribution model of nearest neighbor distance. Ecological Research, 2013, 28: 397-405.

[6]Gao M, Wang X X, Wang D. Species spatial distribution analysis using nearest neighbor methods: aggregation and self-similarity. Ecological Research, 2014, 29: 341-349.

[7]Wiegand Thorsten, Moloney Kirk A. Rings, circles, and null models for point pattern analysis in ecology. Oikos, 2004, 104(2): 209-229.

[8]Pielou E C. A single mechanism to account for regular, random and aggregated populations. Journal of Ecology, 1960, 48:575-584.

[9]戴小华, 余世孝. GIS支持下的种群分布格局分析. 中山大学学报(自然科学版), 2003, 42: 75-78.

[10]Picard Nicolas, Kouyaté Amadou M, Dessard Hélène. Tree density estimations using a distance method in Mali Savanna. Forest Science, 2005, 51(1):7-18.

[11]Clark Philip J, Evans Francis C. Distance to nearest neighbor as a measure of spatial relationships in populations. Ecology, 1954, 35(4):445-453.

[12]Stoyan Dietrich, Penttinen Antti. Recent applications of point process methods in forestry statistics. Statistics Science, 2000, 15:61-78.

[13]Thompson H R. Distribution of distance to n-th nearest neighbor in a population of randomly distributed individuals. Ecology, 1956, 37(2):391-394.

[14]Eberhardt L L. Some developments in distance sampling. Biometrics, 1967, 23:207-216.

[15]Magnussen Steen, Kleinn C, Picard N. Two new density estimator for distance sampling. European Journal of Forest Research, 2008., 127(3):213-224.

[16]Magnussen Steen, Fehrman Lutz, Platt William J. An adaptive composite density estimator for k-tree sampling, European Journal of Forest Research, 2012, 131(2): 307-320.

[17]Richard Condit, Peter S Ashton, Patrik Baker, Sarayudh Bunyavejchewin, Savithri Gunatilleke, Nimal Gunatilleke, Stephen P Hubbell, Roin B Foster, Akira Itoh, James V Lafrankie, Hua Sen Lee, Elizabeth Losos, N Manokaran, R Sukumar, Tauo Yamakura. Spatial patterns in the distribution of tropical tree species. Science, 2000, 288(5470):1414-1418.

[18]Diggle Peter J. Statistical analysis of spatial point patterns,2nd ed. London: Arnold, 2003.

[19]Magnussen S, Picard N, Kleinn C. A Gamma-Poisson distribution of point to k nearest event distance, Forest Science, 2008, 54(4):429-441.

[20]He F L, Duncan R P. Density-dependent effects on tree survival in an old-growth Douglas fir forest. Journal of Ecology, 2000, 88(4): 676-688.

[21]周明, 孙树栋. 遗传算法原理与应用. 北京：国防工业出版社, 1999.

[22]MATLAB Tutorial, The MathWorks http://www.mathworks.cn.

[23]He F L, Gaston K J. Estimating species abundance from occurrence. American Naturalist, 2000, 156(5):553-559.

[24]Hui C, Veldtman Ruan, McGeoch Melode A. Measures, perceptions and scaling patterns of aggregated species distributions. Ecography, 2010, 33(1):95-102.

[25]Dungan J L, Perry J N, Dale M R T, Legendre P, Citron-Pousty S, Fortin M J, Jakomulska A, Miriti M, Rosenberg M S. A balanced view of scale in spatial statistical analysis. Ecography, 2002, 25(5):626-640.

Nearest neighbor distance in spatial point patterns of plant species-probability distribution model and parameter estimation

GAO Meng*

KeyLaboratoryofCoastalEnvironmentalProcessesandEcologicalRemediation,YantaiInstituteofCoastalZoneResearch,ChineseAcademyofSciences,Yantai264003,China

In ecology, the spatial point pattern, which is obtained by mapping the locations of each individual as points in space, is a very important tool for describing the spatial distribution of species. There are three generally accepted types of spatial point patterns: regular, random, and aggregated. To detect spatial patterns, quadrat sampling is commonly applied, where quadrats are randomly thrown on the space and then the number of individuals in quadrats is used to fit Poisson model or NBD model, respectively. Distance sampling is an alternative method for spatial point pattern analysis, which is flexible and efficient, especially in highly dense plant communities, and in difficult terrain. Nearest neighbor method is one effective distance sampling method in spatial distribution pattern analysis. There are two kinds of nearest neighbor distances (NND): point-to-tree NND, distances from randomly selected points (sampling points) to the nearest individuals; and tree-to-tree NND, distances from selected individuals to their nearest neighbors. In this paper, we show a probability distribution model of higher order nearest neighbor distance (tree-to-tree). As we see the expression of this model is complicated; therefore, parameter estimation using conventional method is not a trivial task. In statistics, there are many numerical methods for estimating the parameters of complicated probability distribution model such as moment method, empirical method, graphical method, and maximum likelihood method. In previous literature, maximum likelihood method has been applied for parameter estimation and the optimized estimates on the log-likelihood surface were searched by Nelder-Mead algorithm. However, maximum likelihood estimation was fraught with nontrivial numerical issues when the samples of tree-to-tree distance were rare. In this paper, we use an alternative method, genetic algorithm, to estimate the two model parameters. The computation can be further simplified by defining a suitable objective function based on the expectation and variance. The probability distribution model is then used to fit spatial distribution data of three tree species on southern Vancouver Island, western coast of Canada. It is found that the proposed probability distribution model can fit nearest neighbor distance samples well for Douglas-fir (Pseudotsugamenziesii) and western hemlock (Tsugaheterophylla). For tree species western red cedar (Thujaplicata), the fitting is not so satisfied because individuals of western red cedar are usually distributed as small clusters. As Douglas-fir is almost randomly distributed in space, the estimated parameter representing spatial aggregation nearly does not change. However, the estimated parameter increases when spatial scale increases for the other two tree species, western hemlock and western red cedar. A short discussion about the advantages and limitations of the probability model and its parameter estimation methods is also presented. Theoretically, the probability distribution model presented in this study is applicable to all kinds of spatial point patterns ranging from highly aggregated to complete random. However, as the actual point patterns of tree species usually deviate from theoretical assumptions, the probability distribution model has a few shortcomings such as scale dependence. To gain a better fitting, higher orders of nearest neighbor distances are needed. A balance between field work burden and performance of model fitting should be considered. We suggest that ideal orders of nearest neighbor distances are from 2 to 6. Another potential that can improve the fitting performance is using mixed probability distributions.

spatial point pattern; aggregated distribution; parameter optimization; genetic algorithm

国家自然科学基金项目(31000197, 31570423)；中国科学院知识创新工程项目(KZCX2-EW-QN209)

2014-12-18; 网络出版日期:2015-10-30

Corresponding author.E-mail: mgao@yic.ac.cn

10.5846/stxb201412182517

高猛.植物空间分布格局中邻体距离的概率分布模型及参数估计.生态学报,2016,36(14):4406-4414.

Gao M.Nearest neighbor distance in spatial point patterns of plant species-probability distribution model and parameter estimation.Acta Ecologica Sinica,2016,36(14):4406-4414.