大跨越架空输电导线钢芯铝股应力分布特性研究

黄欲成　陈　池　汪　峰　赵全江　柏晓路　文晓旭

(1. 中南电力设计院有限公司， 武汉　430071； 2. 三峡大学 土木与建筑学院， 湖北 宜昌　443002)



大跨越架空输电导线钢芯铝股应力分布特性研究

黄欲成1陈池2汪峰2赵全江1柏晓路1文晓旭2

(1. 中南电力设计院有限公司， 武汉430071； 2. 三峡大学 土木与建筑学院， 湖北 宜昌443002)

准确评估输电导线运行张力的分层特性是大跨越输电导线选型设计的重要问题．以大跨越架空用特强钢芯高强铝合金AACSR-EST500/230型导线为例，考虑股线泊松比影响，提出了大跨越输电导线股线轴向张力计算方法，建立了大跨越输电导线三维结构有限元实体模型，通过耦合同层和相邻层节点模拟各层股线之间的接触边界条件，重点研究了运行张力作用下输电导线钢芯和铝股的空间应力分布规律，并与理论结果对比分析，探讨了导线比载与钢芯铝股张力比的相关关系．结果表明：在轴向张力作用下，钢芯承担了约60%张力，铝股共承担了40%张力，其张力比约为3∶2，且钢芯和铝股的张力从内至外各自呈增大趋势；大跨越输电导线在悬挂点处的铝股应力强度高于跨中，距离悬挂点越近，股线应力受边界约束影响越大；输电导线相邻层股线的轴向应力峰值呈现相位差；随着导线比载的增加，钢芯和铝股的张力比呈增大趋势．

大跨越架空输电线；钢芯铝绞线；有限元模型；应力分布；张力比

大跨越架空输电导线具有跨越能力强、悬挂点高、档距大等特点，是特高压输电线路跨越湖泊、海峡的重要工程．其典型构造是由多根高强度钢芯和铝合金股线绞制而成，钢芯和铝股共同承担张力．目前我国输电导线设计规范采用整根导线的平均应力进行导线寿命评估和选型设计，忽略了导线钢芯和铝股各层空间应力分布特性．实际上由于两种材料的弹性模量、股线捻角、空间螺旋形态不同，钢芯和铝股应力分布十分复杂，在风雨、覆冰作用下导线线夹出口会产生应力集中，导致疲劳断股．实践表明，服役期输电导线张力分层特性制约着导线的使用寿命．如2008年，衡阳至长沙的500 kV船星I线中的导线在线夹出口附近铝股线全部断裂[1]．2013年对某电站进行巡视时发现多股铝线发生了断股现象，影响了输电线路的安全运营[2]．

针对不同档距的输电导线钢芯和铝股力学特性，国内外学者开展了广泛研究．文献[3]根据平截面假定，建立了导线受拉时各单线所受到的沿绞线轴向方向的纵向力和相邻层之间挤压力的控制方程，推导出了绞线应力的计算方法，并揭示了绞线受拉时应力的分布规律，为推算绞线的机械性能提供了解析方法．Majid Kermani[4]等以覆冰输电导线为对象，运用动力学法求解出导线微风振动方程，并运用ABAQUS有限元软件建立导线节段模型，分析得到导线在径向方向上等效应力的分布．文献[5]在考虑钢芯铝绞线结构特性的情况下，通过ANSYS有限元软件建立了钢芯铝绞线模型，并对有限元模型施加了适当的边界条件，分析了股线的应力应变分布情况．文献[6]以ACSR-720/50型架空导线为研究对象，运用ANSYS软件进行数值模拟，通过单股应力分布、横截面应力状态以及铝股截面等效应力变化规律三个方面来说明导线应力分布规律．文献[7-8]根据微分几何学理论分析钢丝绳股内钢丝的空间位置关系，利用ANSYS软件建立了钢丝绳有限元模型并进行数值模拟，得到了股内各丝的轴向应力、剪应力及轴向变形的分布规律，研究了股内各钢丝受力变形规律．文献[9-10]研究了类似于导线结构的钢丝绳外股层钢丝应力及变形分布规律．

上述研究对象多为普通档距的钢芯铝绞线，钢芯和铝股层数少，捻角小．而大跨越输电线多由高强度镀锌钢芯和外层铝合金股线绞制而成，其钢芯和铝股层数多，螺旋形态复杂，钢芯和铝股应力分布复杂．因此本文以大跨越架空AACSR-500/230型输电导线为对象，考虑导线泊松比，提出轴向张力作用下导线钢芯和铝股承担的张力计算公式．利用耦合同层和相邻层接触的节点模拟各层股线之间的边界条件，建立输电导线的三维结构有限元模型，重点研究输电导线在静张力作用下铝股应力分布特性，并与理论计算结果进行对比．研究结果为大跨越输电导线的疲劳寿命评估和截面选型设计提供理论依据．

1　架空导线分层张力计算方法

大跨越输电导线是由多层高强度钢芯和高强度铝合金股线绕制而成．每层钢股和铝股在空间呈现螺旋状．在运行张力作用下，导线会轴向伸长，但各层之间也相互挤压．为了量化整根导线在轴向力作用下各股线的张力分布规律，通过导线的应力-应变特性，建立单线纵向力的控制方程．同时反映研究问题的本质，作两点假设：(1)同层股线受力状态相同，且各股线的轴心线位于同一圆柱面内；(2)同层股线的螺旋升角变化微小．

单根钢股或铝股线的结构特性由自身相关参数体现，如图1(a)所示．其中股线直径为dn，捻角为αn，每缠绕一周股线旋绕上升的轴向距离为节距ln，截面圆心至第n层股线中心的距离为节圆半径Rn，一个节距内股线的长度为Sn，下标n表示股线层数．同层股线具有相同的dn、αn、Rn，三者关系如下：

(1)

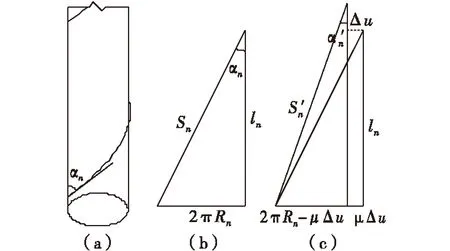
图1　输电导线股丝构造示意图

导线在自重、运行张力等荷载作用下，由于各层股线的长度和空间螺旋形态不同，导线各层股线的应力分配存在差异，且导线股线的力学性能会对整根导线的力学性能产生重要的影响．股线平面展开图如图1中(b)所示，股线拉伸图如1中(c)所示，导线股向伸长量见式(2)：

(2)

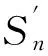
由三角函数关系可得：

(3)

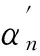
导线股线伸长率εl与轴向伸长率εi分别为：

(4)

由此可知，股线伸长率为：

(5)

导线受轴力作用下，具有相同的轴向伸长率，轴向伸长率εi计算公式为：

(6)

式中，T为作用在整根导线上的轴力；A为整根导线截面面积；E′为整根导线等效弹性模量，计算为：

(7)

式中，EG、EL分别为钢和铝股线的弹性模量；AGn、ALn分别为钢、铝股线第n层的截面面积；βGn、βLn分别为钢、铝股线第n层的捻角．

由图1可知：

(8)

式中，μ为该层股线泊松比．

代入式(5)可得：

(9)

由材料力学可知导线股向应力为：

(10)

式中，En为该层股线弹性模量．

则该层股线轴向张力t为：

(11)

式中，An为该层股线截面面积．

假定绞线受拉后各股无塑性变形，且考虑股线自身因拉伸产生的截面收缩变形即考虑泊松比，忽略挤压变形，可得导线的第n层股线轴向张力：

(12)

式中，下标n表示股线层数；dn为股线直径；zn为股线股数；En为股线弹性模量．

2　大跨越架空导线有限元模型

大跨越钢芯铝绞线从内到外依次为高强度钢芯和铝股，股线以一定的角度紧密缠绕在钢芯外侧，且相邻层的股线螺旋方向相反，最外层绞制方向为右旋．建立模型时，可利用几何相关理论分析输电导线的结构特点及股线的空间螺旋缠绕关系，建立导线的结构有限元模型[11]，并结合导线运行状态，施加边界条件，确定合理的分析类型和计算模式．

2.1模型建立

以大跨越架空输电线AACSR/EST-500/230型导线为对象，该导线由3层高强度钢股和2层高强度铝合金股丝构成．导线结构参数见表1．

表1　AACSR/EST-500/230型导线结构参数

本文建模思路：首先将每根股线视为细长圆柱体，采用ANSYS软件自底向上的建模方法，建立导线各股线的横截面，然后在柱坐标系下，利用螺旋线功能建立各股线的母线，利用拉伸命令将截面沿母线拉伸成实体模型．为减小计算机时，同时考虑约束边界对导线结构应力分布的影响，建立长度为50 mm的三维有限元实体模型，并采用Solid45实体单元，运用六面体单元进行网格划分．单元划分后模型有167 384个节点，134 017个单元，输电导线有限元模型如图2所示．

图2　导线有限元模型

在轴向张力作用下，钢芯和铝股实际上存在接触摩擦效应，考虑到接触对设置量非常巨大，且计算可能出现不收敛．因此本文忽略钢股和铝股间摩擦效应，采用钢股和铝股的节点耦合方法，建立2种有限元模型，研究静张力作用下导线股丝应力分布规律．模型1为只耦合同层股线接触节点的自由度；模型2为分别耦合相邻层、同层股线接触节点的自由度．

2.2边界处理

考虑大跨越输电导线是对称轴向受拉结构，因此在输电导线有限元模型中z=0的端面上约束x、y、z三个方向的自由度．在z=50 mm端面外建立一个刚域点，然后和该端面形成刚域，最后在刚域点上施加运行张力，自重通过施加重力加速度考虑．目前我国大跨越输电导线的运行张力一般为15%～20% RTS(导线额定拉断力)，本文该导线额定拉断力为509.8 kN，本文运行张力按照20%取值，即101.96kN．由于导线工作时，由于导线工作时，股线横截面具有较大的转动，导线受力问题属于大转动小应变几何非线性问题，计算时，在“Analysis Options”区域指定“Large Displacement Static”选项．

2.3有限元模型验证

理论分析中式(12)可计算输电导线每层股线的轴向张力，导线各层股线轴向张力有限元模型结果与理论计算结果见表2，内力与层数关系曲线如图3所示．

表2　钢芯铝绞线各层股线轴向张力(单位：kN)

图3　轴向张力理论值与ANSYS对比图

由表2可知，运行张力作用下，大跨越输电导线内3层钢芯共承担了约60%张力，外层铝芯共承担了约40%的张力，其钢芯和铝股张力比为3∶2，且每层钢芯承受的张力从内至外，呈增大趋势．由于模型中股丝间自由度耦合的处理不同，两种有限元模型的铝部张力趋势不尽相同．在模型2中，外层的铝芯从内至外也是依次增加，但模型1中外层的铝芯依次减小．

由图3可知，模型2的钢芯和铝股张力分布计算结果与理论结果更为吻合．其原因是建立模型2时考虑了相邻层、同层股线接触节点的自由度耦合变形，能够较为准确地模拟导线受力状况．因此，后文采用模型2进行导线截面应力特性分析．通过对比分析可知，对于大跨越输电导线铝股，外层铝股承担的轴向张力比内层大，但在实际工程中，应注意平衡导线外层铝股的导电性和安全性两方面的性能．

3　钢芯和铝股应力分布特性分析

3.1导线横截面应力状态

为研究导线横截面应力沿轴向的变化规律，选取输电导线模型的10个横截面，如图4(a)所示．5号截面应力云图如图4(b)所示．提取各横截面轴线应力的最大值，变化曲线如图5所示．

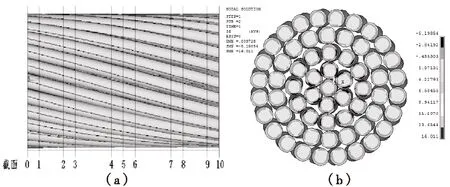
图4　导线横截面位置示意图和5号横截面应力云图

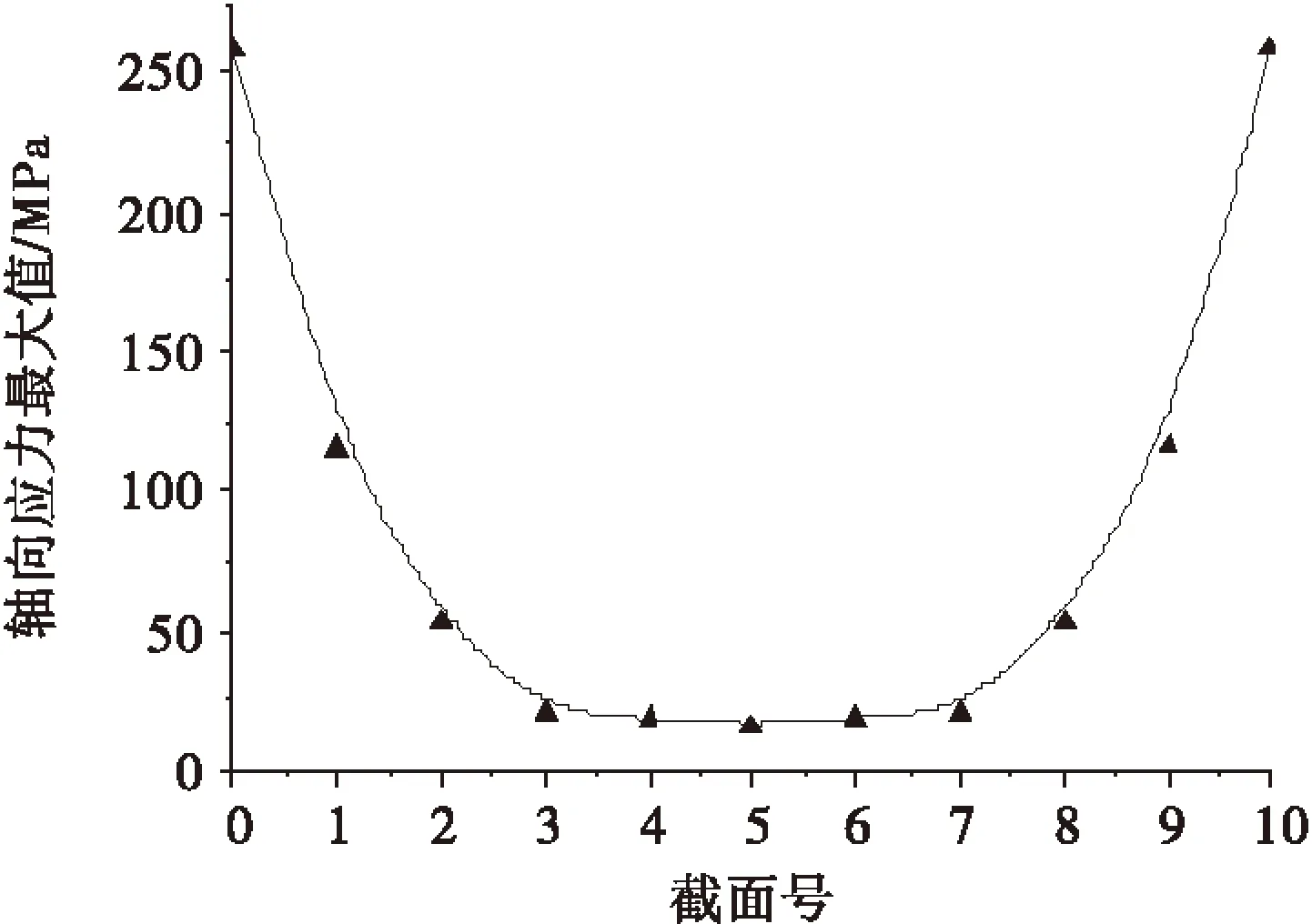
图5　横截面轴向应力最大值变化曲线

由图5可知，导线股线应力强度与股线受约束情况相关，跨中5号截面最大轴向应力仅为16.01 MPa，7号截面最大轴向应力为20.94 MPa，而端部10号截面最大轴向应力为258.32 MPa．由此可知，大跨越输电导线沿轴向截面应力并不均匀．输电导线约束端应力强度明显高于档距跨中的应力强度，距离约束端面越近，股线的应力受端面约束影响越大．该规律与实际工程吻合，大跨越输电导线的悬挂点线夹出口处即为约束端，受力较为复杂，此处应力强度较大，容易发生磨损破坏和疲劳断股．因此建议强化大跨越输电线导线线夹出口处的悬挂设计并定期检查．

3.2导线圆周方向应力分布

导线第3层钢股和第5层铝股轴向应力云图分别如图6(a)和图6(b)所示．输电导线各层股线截面轴向应力沿截面圆周方向的变化曲线如图7所示(远中心轴处为0°/360°)．

图6　导线第3层钢股和第5层铝股轴向应力云图

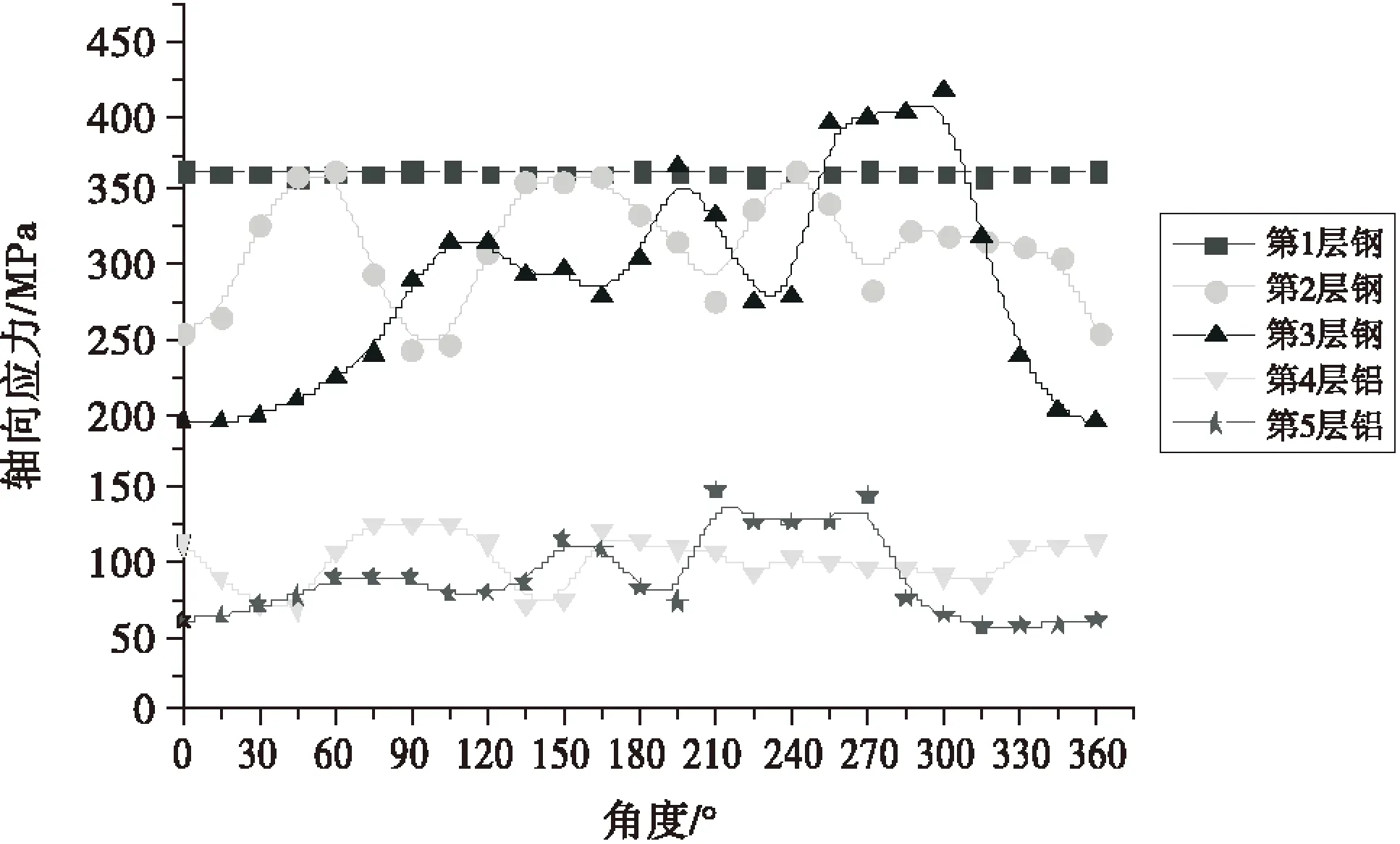
图7　导线模型z=50 mm截面沿圆周的轴向应力

由图6可知，每根股丝沿轴向的应力分布不均匀，两端较大，中间较小．其原因是两端应力受到边界条件的影响．第3层钢芯最大轴向应力比第5层的铝芯应力大．由图7可知，导线内3层钢芯应力强度大于外两层铝．第1层钢芯圆周方向的强度最大，第2层和第3层次之，第3层钢股在247～300°之间的轴向应力稍大于中心钢股轴向应力，分析原因是有限元模型中施加节点自由度耦合造成局部的应力集中．当第2股线轴向应力处于峰值时，则第3股线的轴向应力则为最小值，第4层与第5层间也有类似规律．说明输电导线相邻层股线的轴向张力峰值呈现相位差，其原因在于输电导线相邻层绞制方向相反．

由图7可知，对于导线铝股部分，即图中的第4层和第5层，第4层铝股的最大轴向张力为140.90 MPa，第5层铝股的最大轴向张力为147.69 MPa，可知外层铝股的应力水平高于内层的铝股应力水平．因材料的屈服极限与其应力大小有关，因此在轴向拉力作用下外层铝股首先产生失效的可能性较大．因此，对大跨越输电导线材料选择与导线制作时，建议内层铝股可选择导电率较高的铝线，提高输电容量，外层铝股则选择强度较高的铝合金线，以保证输电线安全运行．

3.3不同比载导线张力分层特性探讨

为了明确大跨越输电导线自重比载与钢芯铝股张力比的相关关系．本文选取7种常用的大跨越输电导线型号，并采用上述理论公式，计算了不同自重比载作用下导线钢芯和铝股张力比值，如图8所示．

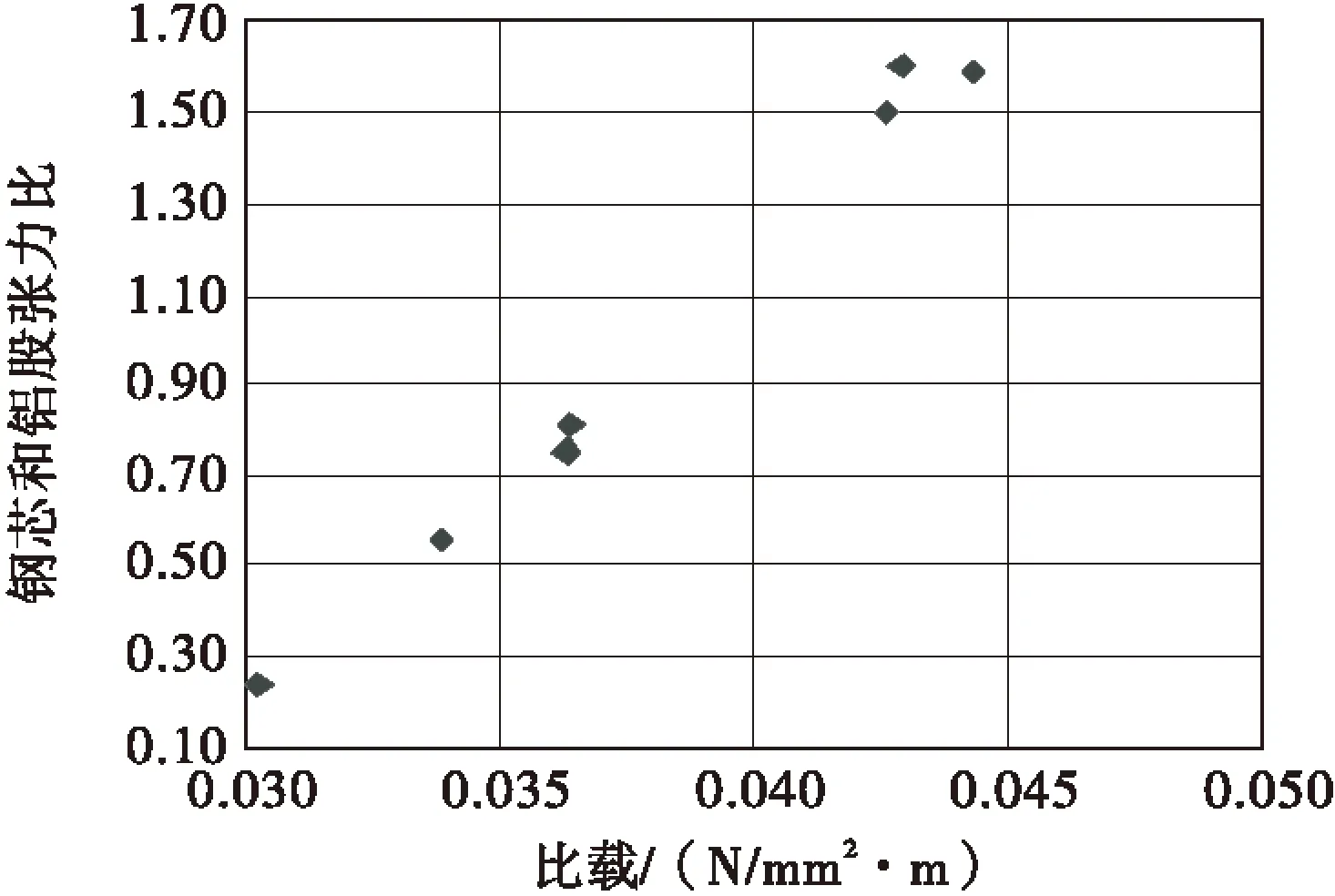
图8　自重比载与钢芯铝股张力比关系图

通过图8可知，不同输电导线的自重比载，钢芯和铝股承担张力比并不相同．例如AACSR-EST500/230型导线，自重比载为0.042 6，钢芯和铝股的张力比值为1.5，而AACSR-EST640/290，自重比载为0.042 9，钢芯和铝股的张力比为1.602 6．随着自重比载的增大，大跨越输电导线钢芯和铝股的张力比呈增大趋势．

4　结　论

本文建立了大跨越架空AACSR-500/230型输电导线三维有限元模型，研究了大跨越输电导线钢芯和铝部应力分布特征．有如下结论：

1)在轴向拉力作用下，大跨越输电导线钢芯承担了约60%的张力，铝芯约40%．其钢芯和铝股张力比约为3∶2，且每层钢芯和铝股承受的张力从内至外，呈增大趋势．

2)输电导线股线截面应力大小与其所受约束距离有关，距约束端越近，则股线截面应力值越大．大跨越输电导线的悬挂点线夹出口处即为约束端，受力较为复杂，建议强化大跨越输电线导线线夹出口处的悬挂设计并定期检查．

3)输电导线相邻层股线的轴向张力峰值呈现相位差，在轴向拉力的作用下外层铝股首先发生失效的可能性较大．在输电导线材料选择与导线制作时，建议内层铝股选择导电率较高的铝线，提高输电容量，外层铝股则应选择强度较高的铝合金线．

4)随着自重比载的增大，大跨越输电导线钢芯和铝股的张力比呈增大趋势．

5)考虑相邻层、同层股线接触节点的自由度耦合的有限元模型与理论值较为接近，可用于大跨越输电导线张力分层特性分析．

[1]熊亮，刘纯，何德家．500kV输电导线断股分析[J]．湖南电力，2009，29(2)：49-51．

[2]冯砚厅．500kV导线断股原因分析及处理[J]．河北电力技术，2014，33(2)：4-6．

[3]郑黎阳，孙祖志．铝绞线和钢芯铝绞线的应力分析[J]．武汉水利电力大学学报，1997，30(3)：65-68．

[4]Majid Kermani． Masoud Farzaneh. Laszlo E. Kollar. Estimation of Stresses in Atmospheric Ice During Aeolian Vibration of Power Transmission Lines[J]．Journal of Wind Engineering and Industrial Aerodynamics， 2010：592-599．

[5]秦力，李军阔，付强．输电线路钢芯铝绞线股线力学特性研究[J]．水电能源科学，2013，31(5)：194-197．

[6]马行驰，何大海，朱瑞．ACSR-720/50型架空导线单股应力状态分析[J]．电线电缆，2013，3(3)：13-16．

[7]马军，葛世荣，张德坤．钢丝绳应力及股内钢丝变形的相关性研究[J]．煤炭科学技术，2009，37(3)：73-76．

[8]马军，葛世荣，张德坤．钢丝绳股内钢丝的荷载分布[J]．机械工程学报，2009，37(3)：73-76．

[9]吴娟，寇子明，刘玉辉．独立钢丝绳芯钢丝绳应力及变形分布[J]．煤炭学报，2014，39(11)：2340-2347．

[10] 陈向阳，张瑾．1×7+IWS结构钢丝绳服役中的有限元模拟[J]．铸造技术，2014，35(4)：676-678．

[11] 王桂兰，张海鸥．钢丝绳成形过程共转坐标系弹塑性有限元分析[J]．华中科技大学学报，2001，29(8)：65-67．

[责任编辑张莉]

Stress Distribution Characteristics of Steel Core and Aluminum Strand of Large Span Overhead Transmission Line

Huang Yucheng1Chen Chi2Wang Feng2Zhao Quanjiang1Bai Xiaolu1Wen Xiaoxu2

(1. Central Southern China Electric Power Design Institute Co.， Ltd., Wuhan 430071, China; 2. College of Civil Engineering & Architecture, China Three Gorges Univ., Yichang 443002, China)

It is important to accuratly evaluate tension distribution of transmission line for type section design of large span overhead transmission line. Taking AACSR-EST500/230 wire for example, the calculation method of axial tension is purposed considering Poisson ratio effect. The three-dimensional finite element model of transmission line is established. Through coupling with layers and the adjacent layer nodes to simulate contact boundary conditions of each layer strands, the space stress distribution of steel core and aluminum strand under running tension is researched and compared to theoretical analysis. Finally, the correlation between unit-area weight and tension ratio is analyzed. The results show that the steel core bearing tension is about 60% and aluminum strand is 40%; the tension ratio is about 3∶2. The bearing tension of steel and aluminum strand is increasing from the inside to the outside. The stress intensity of the suspension point is higher than midspan for large span transmission line. Closer the suspension point is, the greater the stress is affected by the boundary constraint. The peak stress of the adjacent layer of the transmission line is in the phase difference, and the stress level of the outer layer is greater than inner. With the increase of the unit-area weight of wire, the tension ratio of the steel core and aluminum wire is increasing.

large span overhead transmission line；aluminum cable steel reinforced；finite element model；stress distribution；tension ratio

2016-05-17

中国电力工程顾问集团公司科技项目(DG1-D10-2014)

黄欲成(1979-)，男，高级工程师，主要从事输电线路电气设计．E-mail： huangyucheng@csepdi.com

10.13393/j.cnki.issn.1672-948X.2016.04.016

TM726.3

A

1672-948X(2016)04-0076-06