桩周土开挖条件下钢管桩屈曲稳定性试验研究

贾强，栾树， 李际平，张鑫

(1.山东建筑大学 土木工程学院，山东 济南，250100；2. 山东省建筑结构鉴定加固与改造重点实验室，山东 济南，250100)



桩周土开挖条件下钢管桩屈曲稳定性试验研究

贾强1,2，栾树1,2， 李际平1,2，张鑫1,2

(1.山东建筑大学 土木工程学院，山东 济南，250100；2. 山东省建筑结构鉴定加固与改造重点实验室，山东 济南，250100)

既有建筑物增设地下空间时，需要运用桩基础支撑上部建筑物，才可开挖建筑物下面的土方。随着桩周土减少，桩的屈曲稳定性会相应减少。文章在模型箱内利用杠杆加载的方式对不同开挖深度条件下的钢管桩的屈曲承载力进行了研究和测试，分析了其相应的稳定系数。结果表明：当桩顶加载达到极限荷载时，桩身会出现突然的屈曲破坏；开挖比较小时，屈曲位置出现在桩土交界面附近，随着开挖比的增加，屈曲位置明显上移；随着桩周土开挖深度增加，桩的稳定系数随之减小，当钢管桩下端处于嵌固状态时，其稳定系数比处于非嵌固状态时明显要大；钢管桩中部增设了水平拉接杆件后，其稳定性明显提高；桩周土的开挖比>0.5时，回转半径较大的钢管桩稳定性系数较大；当其值<0.5时，回转半径较大的钢管桩稳定性系数较小。

桩周土开挖；屈曲稳定性；稳定系数

0　引言

目前，有序、合理、综合、高效地开发利用既有建筑物地下空间资源，成为扩充基础设施容量，提高城市综合防灾能力，提高土地利用效率与节约土地资源的最为有效的途径之一[1]。既有建筑物地下空间开发的核心技术是桩基础托换和土方开挖。在既有建筑物下方兴建地下室时，需要运用原桩基础或增设新的桩基础支撑上部建筑物，才可开挖建筑物下面的土方[2]。土方开挖过程中，随着桩周土减少和桩基础的暴露，被开挖托换桩周边侧阻力相应减少，同时桩周土的挖除会减少对桩的水平约束，进而降低其稳定性[3-4]。

在北京市音乐堂改建工程中，将独立柱基础框架结构的观众厅新增一层高为6.5 m的地下室。为了防止桩基失稳，选用了深为8 m的人工挖孔端承桩的方案，其桩径达到1 m[5]。淮安15层(局部17层)框—剪结构商住楼，采用长度为21 m、直径为0.8和1 m两种钻孔灌注桩支撑上部结构，增设两层地下室[6]。济南商埠区某历史建筑地下增层中，采用了微型钢管桩托换支撑既有建筑的方案，为了保证桩的稳定性，桩周土每开挖一定深度，钢管间就设置一道拉结支撑杆件[7]。在此类既有建筑地下增层工程中，由于托换荷载大，如何保证桩周土开挖过程中托换桩的稳定性成为关键技术问题。

目前，对埋置在土体中的混凝土桩在计算桩身轴心抗压强度时，一般不考虑压曲的影响，即取稳定系数φ=1.0，但对于上部处于没有土体约束的自由状态的高承台桩，应对桩的压曲稳定性进行验算。JGJ 94—2008《建筑桩基技术规范》[8]第5.8.4条的规定，应根据桩顶约束情况、桩身露出地面的自由长度、桩的入土长度、桩侧和桩底的土质条件确定桩身压屈计算长度。早在 20世纪20年代，Forsesn提出了拼柱式高桥墩的稳定性研究难点在于桩周土体的约束作用不易确定，胡人礼首先基于“m”法提出一组桩身计算长度的经验计算公式，现仍被有关规范采用[9]。之后,许多学者采用引入最小势能原理、变分法、伽辽金法能量法等对桩的屈曲稳定性进行了理论研究[10-12]。另有部分学者采用钢轨桩、钢管桩、铜桩、木桩以及铝桩对桩的屈曲稳定性进行试验研究，取得大量的研究成果[11-13]。贾强等针对地下增层中钢管托换桩的受压稳定性进行了初步试验研究，提出了底端固定、顶端铰接的钢管计算长度系数为0.616。但该试验缺少不同开挖深度的对比试验数据[12-14]。

文章针对桩周土体开挖卸荷条件下的钢管桩桩身稳定性进行试验研究，通过测试桩身极限承载力及应力分布规律，分析不同开挖深度和不同的约束形式对钢管桩屈曲稳定性的影响，提出其稳定性系数，为地下增层托换桩的设计提供理论支持。

1　模型试验的准备

1.1模型箱设计

试验模型箱边长为1 m×1 m、高为1.5 m上面开口，由三块厚度为10 mm的钢板和L75×5的等边角钢组装焊接而成。为了装卸土方便，箱体一侧安装可拆卸式挡板，挡板对面钢板顶端焊接一U型套箍，作为杠杆加载装置的支点。模型箱示意图如图1所示。

1.2试验加载装置

文中试验采用杠杆加载法，杠杆由2个16号槽钢对焊而成，一端穿入箱顶套箍内，中部通过套管向钢管桩加载，杠杆荷载放大系数为3，加载装置示意图如图2所示。

1.3钢管桩的选用

根据工程中常用钢管桩长径比，选用试验桩桩长分别为1.2 m，外径分别为16和20 mm，壁厚为1.0 mm，材料强度等级为Q235。为准确获得钢材的极限抗拉强度值，在钢管上截取材料加工成宽度为4 mm、长度为400 mm的三组试件进行拉伸试验，得到其极限抗拉强度见表1。

在桩侧面垂直于杠杆加载平面上粘贴应变片，沿桩身等间距(200 mm)布设，通过静态应变仪测出钢管桩桩身应变(如图3所示)。

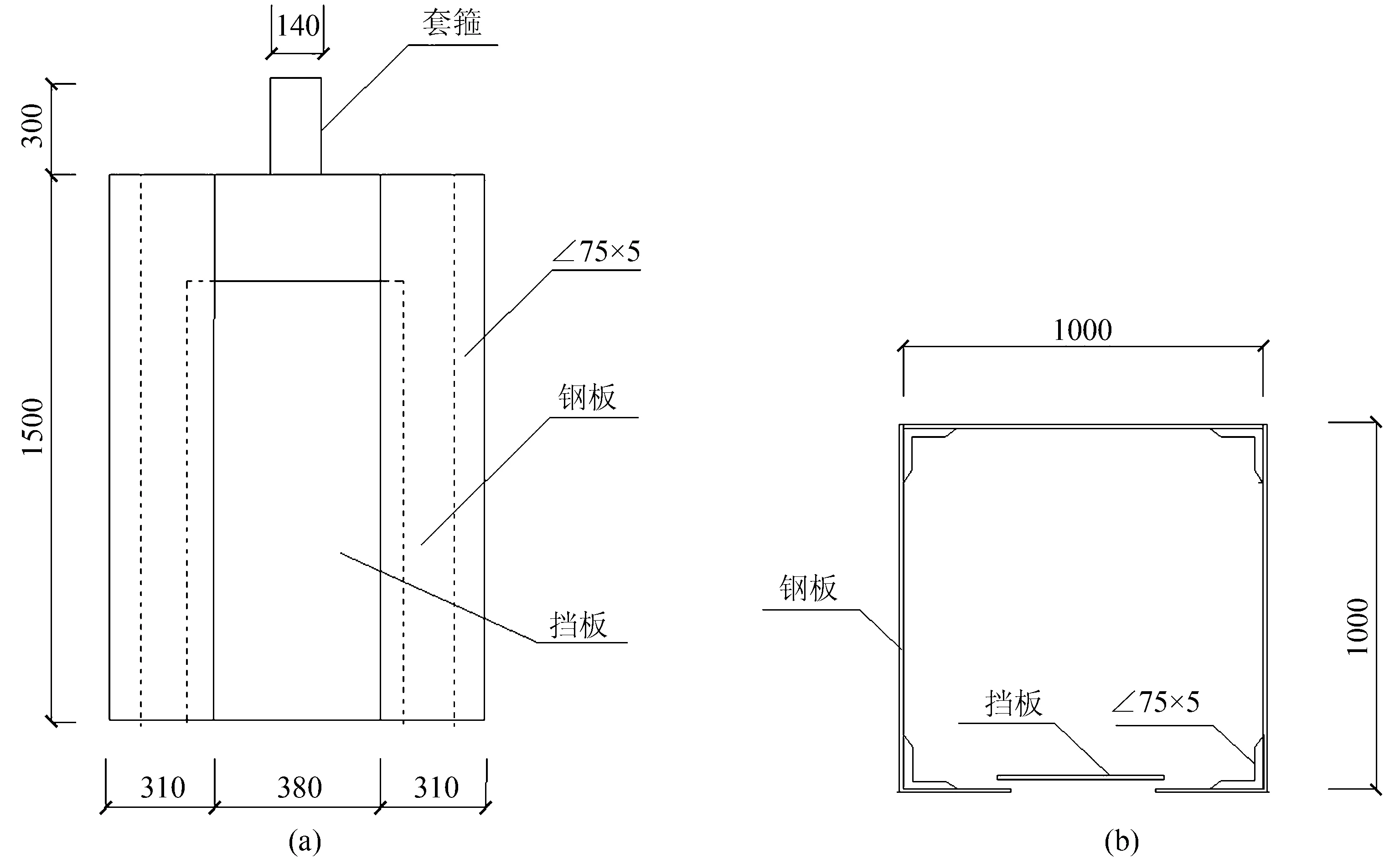
图1　模型箱示意图/mm(a) 平面图;(b) 立面图

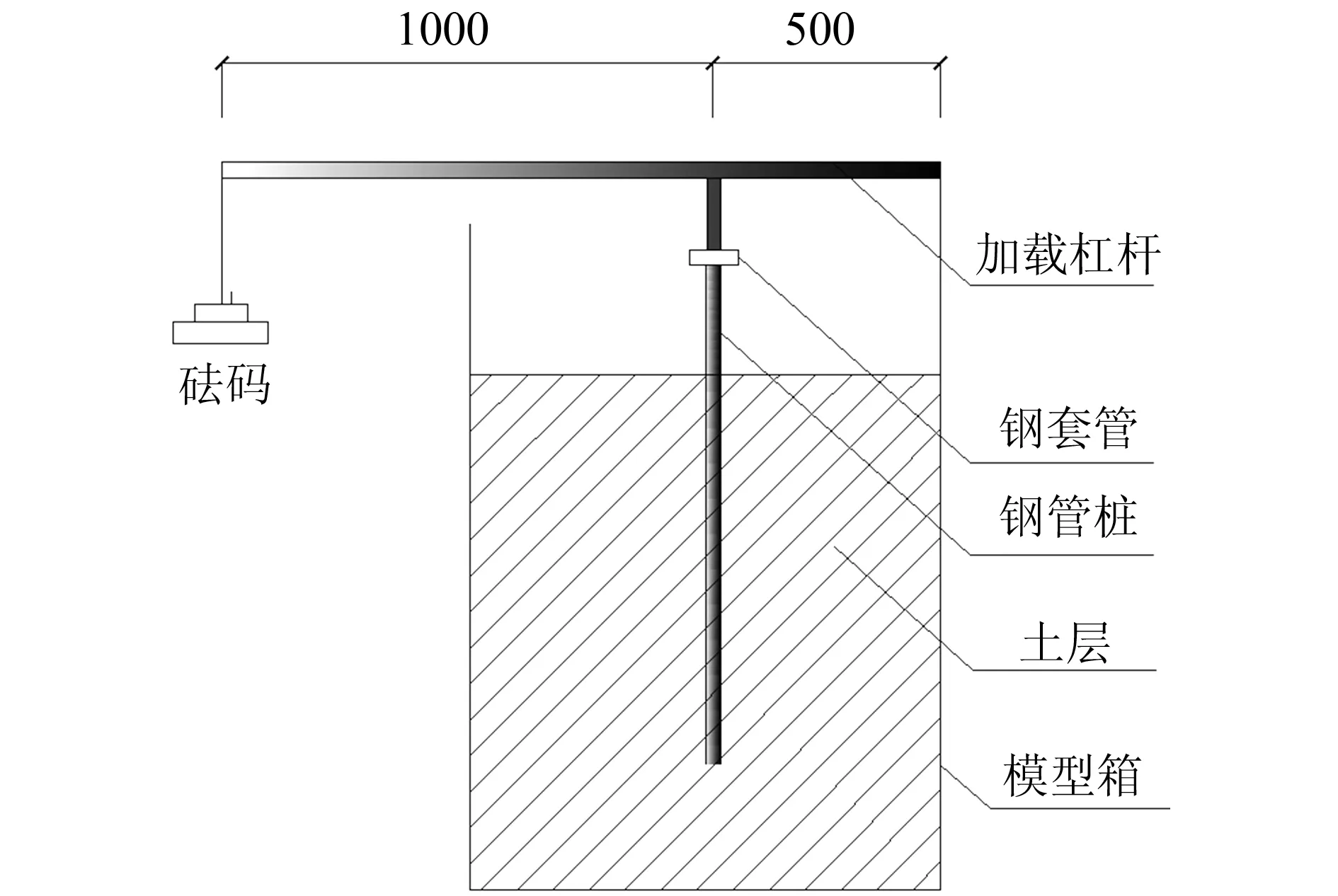
图2　加载装置示意图/mm

图3　桩身应变片布置图

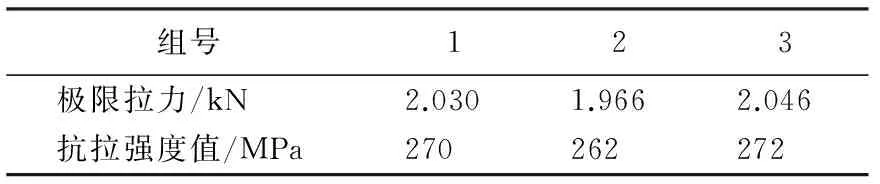
组号123极限拉力/kN2.0301.9662.046抗拉强度值/MPa270262272

1.4桩周土参数

桩周土选用中砂，其物理力学参数见表2。为测试代表桩周土对钢管桩的约束程度的水平抗力系数的比例系数，将桩长1000 mm钢管桩埋入模型箱，在桩顶通过弹簧测力计施加水平拉力，用百分表测得桩顶位移，得到桩的水平力—位移曲线如图4所示。

利用JGJ 94—2008《建筑桩基技术规范》[8]附录E.0.8条公式，计算得到桩周土的水平抗力系数的比例系数值为6.93 MN/m4。

表2　桩周土物理力学参数

1.5试验工况

钢管桩桩长1.2 m，桩周土的开挖深度分别为0、0.35、0.55、0.75和1.20 m，相应开挖深度与桩长的比值(以下简称“开挖比”)为0、0.29、0.46、0.63和1。桩两端的约束方式：桩的顶端通过转轴于杠杆相连，可视为铰接；桩的底端有非嵌固和嵌固两种

方式，非嵌固是将钢管插入焊接在底板的短钢筋上，嵌固则上将钢管下端围焊在边长为0.8 m的正方形钢板上。另外，为了验证在桩顶部和桩身中部设置水平拉接杆件对于提高桩身稳定的有效性，模型箱对角线方向焊接钢筋在两侧对桩身形成约束(如图5所示)。

图4　桩的水平力-位移关系曲线图

图5　桩身中部增设水平拉接杆件图

1.6加载方法

试验用砝码和砂袋加载。加载水平在预估屈曲极限荷载80%以下时，每级加载量为极限荷载的10%；超过80%后每级加载量为极限荷载的5%。每级加载待静态应变仪读数稳定后5 min读取应变值，记录数据后再进行下一级的加载。

2　试验结果及分析

2.1试验现象

当桩顶加载达到极限荷载时，桩身出现突然屈曲破坏。开挖比较小时，屈曲位置出现在桩土交界面附近(如图6所示)；随着开挖比的增加，屈曲位置明显上移。

2.2桩身应变

通过静态应变仪测试了桩身不同埋深处的荷载与应变关系曲线。其中，桩长为1.2 m、外径为16 mm、壁厚为1 mm的钢管桩，约束形式为上端铰接，下端非嵌固，桩周土开挖350 mm桩顶荷载—应变曲线图如图7所示。

图6　钢管桩的屈曲破坏位置图

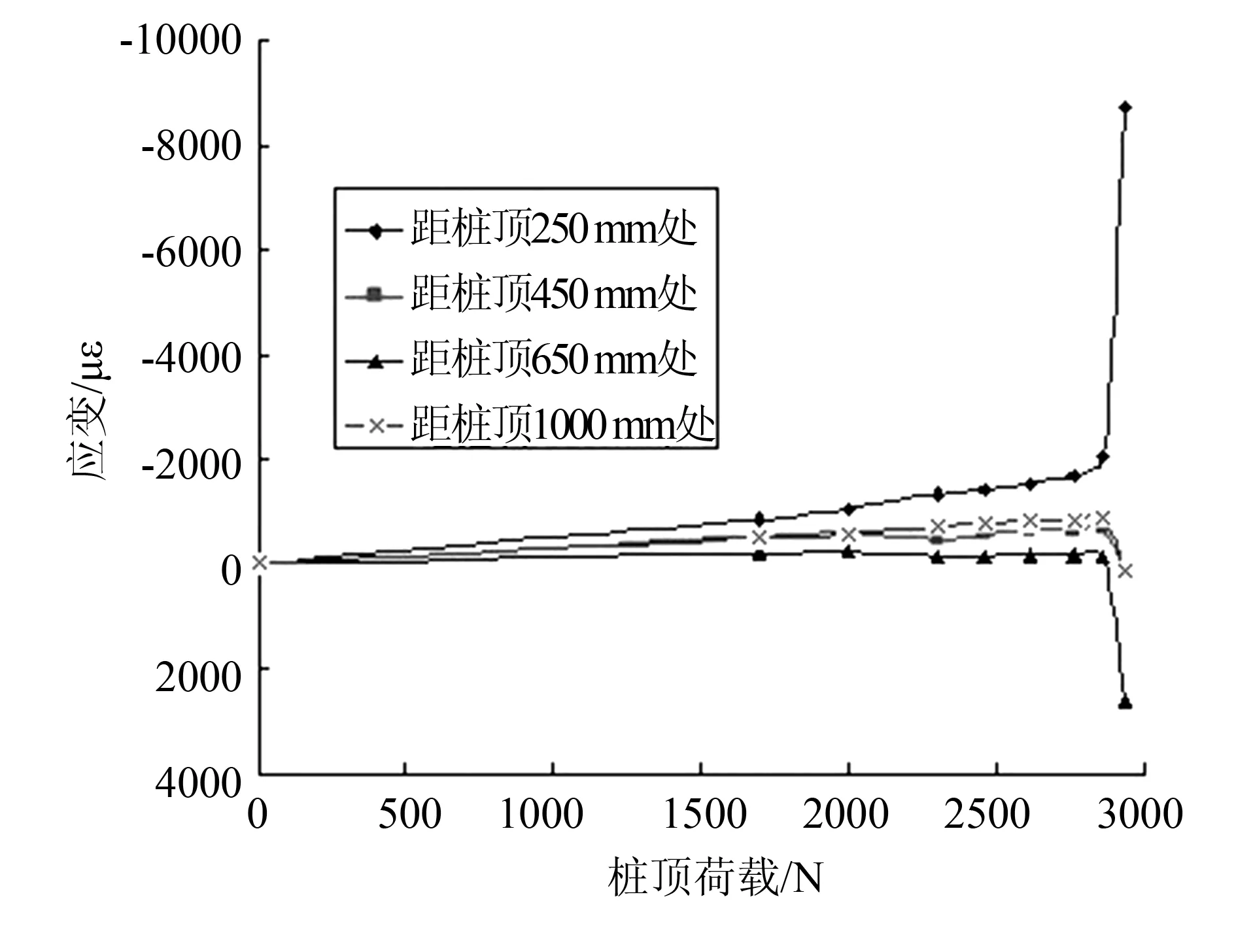
图7　桩身荷载—应变曲线图

从图7可以看出，在桩顶荷载达到极限荷载之前，钢管桩的荷载应变关系为线性增长，当桩顶荷载达到极限荷载时，屈曲位置附近的应变急剧增加。

2.3钢管桩稳定系数影响因素分析

GB 50017—2003《钢结构设计规范》中[15]，轴心受压构件的稳定性按式(1)计算为

(1)

式中：N为轴心压力，N；A为截面面积，m2；f为材料强度，Pa；φ为稳定性系数。

通过试验得到钢管桩的受压极限荷载，以及钢管截面面积和实测材料强度，可反算出桩的稳定性系数。

不同组合工况下，不同开挖比的桩顶极限荷载、稳定系数等试验和计算结果见表3。

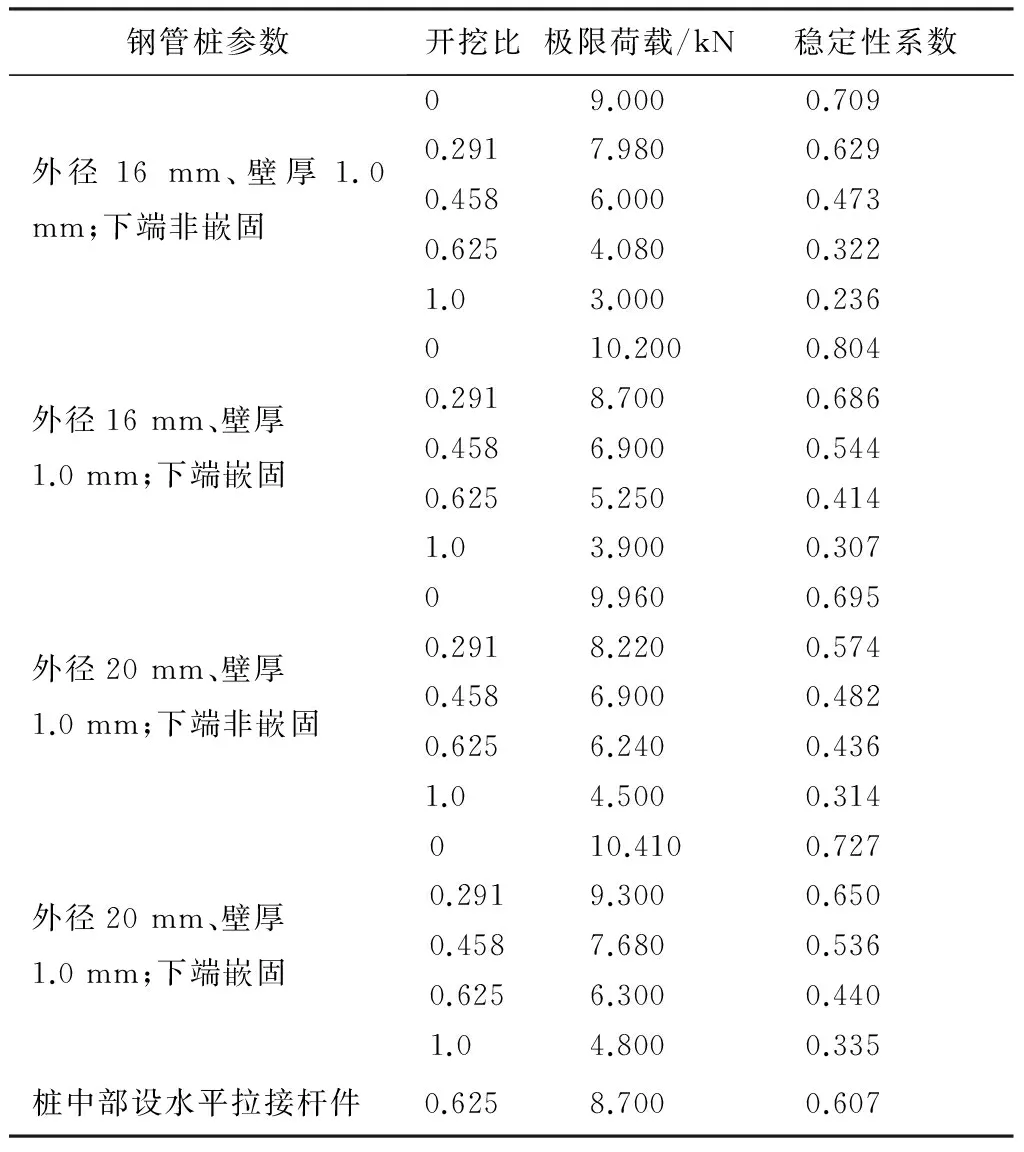
表3　钢管桩不同开挖比稳定性试验和计算结果

将表3中不同回转半径钢管在桩底为非嵌固和嵌固两种约束状态下的稳定系数—开挖比关系绘制成曲线，如图8(a)、(b)所示。

2.3.1开挖比

通过图8的曲线可以看出，随着开挖比的增加，钢管桩的稳定系数明显下降。这说明桩周土的约束作用明显提高了桩的稳定性。

2.3.2桩端和桩身约束

比较图8可知，桩下端处于嵌固状态时，稳定系数比处于非嵌固状态时明显要大。这说明钢管桩下端嵌固在岩石中，对提高其稳定性明显是有利的。

钢管桩中部增设了水平拉接杆件后，在相同的开挖比(0.625)和桩底约束条件下，稳定性系数提高了1.39倍。这是由于增设水平拉接杆件后，钢管桩的计算长度明显减少，从而减少了长细比，提高了稳定性系数。

2.3.3回转半径

从图8中还可以看出，在桩周土的开挖比较大时(>0.5)，回转半径较大的钢管桩稳定性系数较大。这是因为开挖比大时，桩周土的约束明显减弱，相同的计算长度回转半径较大的钢管长细比小，稳定性系数较高。相反，桩周土的开挖比较小时(<0.5)，回转半径较大的钢管桩稳定性系数较小。此时，钢管大部分埋在土体中，桩周土对钢管的约束明显。外径为20 mm的钢管与外径为16 mm相同壁厚(1 mm)的钢管相比，回转半径增大了1.26倍，而其抗弯刚度增大了2.03倍。因此，达到临界荷载前外径大的钢管引起的深层土体中的变形小，桩周土的约束力小，其稳定性系数相应变小。

事实上，影响钢管桩稳定性的因素不仅仅是开挖比、回转半径、两端约束和增设水平拉接杆件等，桩周土的水平抗力系数也是重要因素，但本试验仅选用了砂质土，其他类型土对桩稳定性的影响需做进一步的试验研究。

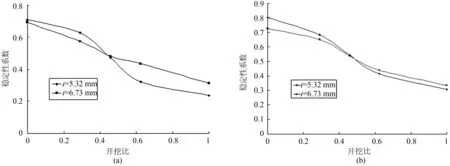
图8　不同回转半径钢管桩的稳定性系数—开挖比关系曲线图(a)桩底非嵌固；(b)桩底嵌固

3　工程验证

济南皮肤病医院位于济南市中山公园东老商埠一期地块内，为单层带局部地下室的砌体结构，建筑面积约165.08 m2，为仿德式历史风貌建筑(如图9所示)。山东融汇建设开发有限公司在对该地块开发的同时，拟对该建筑原址保护，并在其下方增设三层地下停车场[7]。

图9　济南皮肤病医院南立面图

工程共使用48根直径为146 mm、壁厚为12 mm的无缝钢管支撑上部结构，钢管长度为15 m(下端进入中风化岩层1 m)。支撑钢管和墙体托换梁的平面布置图如图10所示。为了保证土方开挖过程中钢管桩的稳定性，对开挖过程进行了数值模拟，并借鉴了本试验结果，提出了每向下开挖2.5 m，在钢管间设置一道水平和斜向的拉结支撑杆件的设计方案。土方开挖至底板设计标高，施工现场情况如图11所示。在桩周土开挖过程中，用光栅应变计对钢管的应力变化进行观测，结果在31.3～46.4 N/mm2范围内，其值远小于钢管强度设计值215 N/mm2。

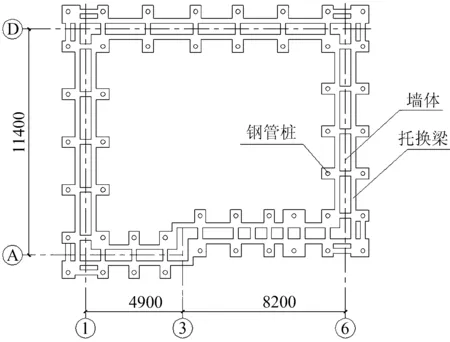
图10　钢管桩和托换梁平面布置图/mm

图11　土方开挖至底板设计标高的施工现场图

4　结论

通过上述研究可知：

(1) 开挖比较小时，钢管桩受压屈曲位置出现在桩土交界面附近；随着开挖比的增加，屈曲位置明显上移。随着桩周土开挖深度增加，其对钢管桩的约束减少，桩的稳定系数随之减小。

(2) 钢管桩下端处于嵌固状态时，其稳定系数比处于非嵌固状态时明显要大。钢管桩中部增设了水平拉接杆件后，其稳定性明显提高。桩周土的开挖比>0.5时，回转半径较大的钢管桩稳定性系数较大；桩周土的开挖比<0.5时，回转半径较大的钢管桩稳定性系数较小。

[1]贾强，王明国，李鹤.板式托换法在既有建筑物地下增层中的应用[J]. 山东建筑大学学报,2010，25(3)：161-165.

[2]贾强，应惠清，张鑫.锚杆静压桩技术在既有建筑物增设地下空间中的应用[J].岩土力学,2009，30(7)：2053-2057.

[3]龚晓南，王继成，伍程杰.深基坑开挖卸载对既有桩基侧摩阻力影响分析 [J].湖南大学学报,2014，41(6)：70-76.

[4]龚晓南，伍程杰，俞峰，等.既有地下室增层开挖引起的桩基侧摩阻力损失分析[J].岩土工程学报,2013，35(11)：1957-1964.

[5]王雅斋，梁新利. 整体基础托换与地下加层施工工法[J]. 施工技术,2002，31(5): 45-46.

[6]陆钧衡.地下加层工程中桩基托换设计施工工艺及若干关键问题研究[D].南京：东南大学，2008.

[7]贾强，张鑫，夏风敏，等. 济南商埠区历史建筑地下增层工程设计与施工[J].山东建筑大学学报,2014，29(5)：464-469.

[8]JGJ 94—2008建筑桩基技术规范[S]. 北京：中国建筑工业出版社，2008.

[9]胡人礼.桥梁桩基础分析和设计[M].北京：中国铁道出版社，1987.

[10]邹新军.基桩屈曲稳定分析的理论与试验研究[D].长沙：湖南大学，2005.

[11]郑刚，张立明，刁钰.开挖条件下坑底工程桩工作性状及沉降计算分析[J].岩土力学,2011，32(10)：3089-3096.

[12]贾强，郑爱萍，张鑫.高承台钢管桩受压稳定性的试验研究和数值分析[J].岩土力学,2011，32(6)：1736-1740.

[13]Zheng A.P., Jia Q.. Application of Steel Micro-piles in Underpinning of Existing Buildings[C].12 th international conference on inspection,Appraisal,Repairs & Maintenance of Structures(ICIARM)，Singapore：Ci-premier Pte Ltd，2010.

[14]贾强，李际平，张全立，等. 桩周土开挖条件下桩基础屈曲稳定性分析[J].山东建筑大学学报,2014，29(6)：497-503.

[15]GB 50017—2003,钢结构设计规范[S]. 北京：中国计划出版社，2003.

(学科责编：吴芹)

Experimental study on steel pipe pile bucking stability under excavation conditions

Jia Qiang1,2，LuanShu1,2，Li Jiping1, 2，etal.

(1. School of Civil Engineering, Shandong Jianzhu University, Jinan 250101, China；2. Shandong Provincial Key Laboratory of Appraisal and Retrofitting in Building structures, Jinan 250100, China)

The underpinning pile can be used to support the existing building for construction of basement. The soil excavation around the pile can decrease the bearing capacity of piles. The piles bucking stability in different excavation depth was tested in model box by pry bar loading devise. Then, the stability coefficient was calculated. The test results indicate：when the loads on the top of the pile reaching ultimate load, the body of the pile appears the buckling deformation. At the beginning of soil excavation, the buckling location of pile is near the interface of the pile and soil. The deeper soil excavation, the higher location of pile buckling; The stability coefficient decreases with the soil excavation around the pile;the stability coefficient with end build-in is higher than with end non embedded;the stability coefficient of piles increases obviously after the horizontal components installed on the piles;the stability coefficient of piles with high radius of gyration is bigger than with low radius of gyration when the ratio of excavation depth to length of pile over 0.5; on the contrary, the stability coefficient of piles with high radius of gyration is smaller than with low radius of gyration when the ratio of excavation depth to length of pile under 0.5.

soil excavation around the pile; bucking stability; stability coefficient

2015-11-03

国家自然科学基金项目(51278286)；教育部创新团队项目(IRT13075)

贾强(1970-)，男，教授，博士，主要从事建筑物鉴定加固等方面的研究.E-mail:jiaqiang@sdjzu.edu.cn

1673-7644(2016)02-0103-06

TU473

A