X-ss-半置换性对有限群结构的影响
谢凤艳,毛月梅
(1.安阳学院 建筑工程学院, 河南 安阳 455000; 2.大同大学 数学与计算机科学学院, 山西 大同 037009)
X-ss-半置换性对有限群结构的影响
谢凤艳1,毛月梅2
(1.安阳学院 建筑工程学院, 河南 安阳 455000; 2.大同大学 数学与计算机科学学院, 山西 大同 037009)
设X是有限群G的非空子集, 子群H称为在G中X-ss-半置换的, 如果H在G中有一个补充T, 只要(p,|H|)=1,就存在x∈X,使得HPx=PxH, 其中P∈Sylp(T). 研究极小子群和4阶循环子群的X-ss-半置换性对有限群结构的影响, 推广了以往的一些结果.
极小子群;超可解群;X-ss-半置换子群; 饱和群系
文中所有群均为有限群.G表示有限群,U表示所有超可解群的群系.
设H是G的子群.H称为在G中置换的, 如果对G的任意子群K, 有HK=KH. 作为置换子群的推广.s-置换[1]、s-半置换[2-3]、X-置换子群[4]、X-半置换子群[5]、X-s-半置换子群[6]等概念先后被提出. 利用这些概念人们已经得到了许多重要结果[1-9]. 祝明[10]又将s-置换、s-半置换、X-置换子群、X-半置换子群、X-s-半置换子群定义统一推广为X-ss-半置换子群的概念, 并利用Sylow子群的极大子群的X-ss-半置换性刻画群的p-幂零性和超可解性.笔者在文[10]的基础上, 利用Sylow子群的极小子群和4阶循环子群的X-ss-半置换性对包含所有超可解群的饱和群系进行研究, 得到一些结论,推广和改进了一些已知成果.
1 预备知识
定义1[10]设X是G的非空子集, 子群H称为在G中X-ss-半置换的, 如果H在G中有一个补充T, 只要(p,|H|)=1,就存在x∈X,使得HPx=PxH, 其中P∈Sylp(T).
论文用Xss(H)表示子群H在群G中所有满足X-ss-半置换子群定义中补充子群T的集合.
显然所有的s-置换、s-半置换、X-置换、X-半置换、X-s-置换、X-s-半置换子群都是X-ss-半置换子群, 反之不成立[10].
引理1[10]假设H是G的子群,X是G的非空子集,N是G的正规子群. 若H在G中X-ss-半置换的, 则下列断言成立
(1) 若H≤M≤G且X≤M, 则H在M中X-ss-半置换的.
(2) 若H为p-群或者(|H|,|N|)=1,则HN/N在G/N中XN/N-ss-半置换的.
(3) 若T∈Xss(H)且H≤NG(X), 则对任意的g∈G,有Tg∈Xss(H).
(4) 若X≤D≤G, 则H在G中D-ss-半置换的.
引理2[11]设F是包含所有超可解群系的饱含群系,N是G的正规子群且使得G/N∈F.如果N循环, 那么G∈F.
引理3[12]设N是群G的一个非平凡正规子群, 若N∩Φ(G)=1. 则F(N)为G的极小正规子群直积.
引理4[13]设A,B是G的子群且G≠AB. 如果对G的任意元素g,有ABg=BgA. 则G中存在真正规子群N,使得A≤N,或者B≤N.
设F是一个饱和群系.称G的子群H在G中F-可补充, 如果G有一个子群T∈F,使得HT=G.
引理5设F是一个饱和群系,H在G中F-可补充.
(1) 如果H≤M≤G, 则H在M中F-可补充.
(2) 如果N是G的正规子群, 则HN/N在G/N中F-可补充.
证明因为F是一个饱和群系, 所以F对商群及子群封闭, 故(1) 、(2)成立.
2 主要结论及应用
定理1设F是包含U的饱和群系,X是G的可解正规子群. 则G∈F的充分必要条件是G有正规子群E,使得G/E∈F,且E的每个非循环Sylow子群的极小子群和4阶循环子群在G中要么U-可补充, 要么X-ss-半置换的.
证明必要性显然成立, 只需给出充分性的证明. 假设充分性不成立, 选定一个饱和群系F. 设G为极小阶反例, 并令N是G的极小正规子群. 通过下列断言完成定理证明.
(1)G/N∈F.
因为G/E∈F, 所以(G/N)/(EN/N)≅G/EN≅(G/E)/(G/EN)∈F. 设T/N是EN/N的非循环Sylow子群,L/N是T/N的极小子群或者4阶循环子群. 则存在E的非循环Sylow子群P,使得T=PN且P中存在一个素数阶或者是4阶元素x, 使得L=
(2)N是G的唯一极小正规子群且G=[N]M,M为G的一个极大子群.
因为F是一个饱和群系, 所以由(1)知,N是G的唯一极小正规子群且Φ(G)=1. 故存在G的一个极大子群M使得G=[N]M.
(3)N=GF≤E,N为初等交换非循环p-群,其中p为G的某一个素因子.
由(1)和(2)及G/E∈F,得N=GF≤E. 由(1)G/N∈F及引理2知,N非循环. 如果E可解, 则N可解,从而(3)成立. 如果E不可解. 假设E的每个非循环Sylow子群的极小子群和4阶循环子群在G中U-可补充.设K是E的一个真子群, 则K的每个非循环Sylow子群的极小子群和4阶循环子群在G中U-可补充.由引理5(1)知,K的每个非循环Sylow子群的极小子群和4阶循环子群在K中U-可补充.又因为K/K∈U, 所以K满足充分性条件. 由G的极小选择,K为超可解群. 从而E为极小非超可解群. 由文[12]得E可解, 这一矛盾说明存在E的非循环Sylow子群的极小子群或4阶循环子群, 记为H, 在G中没有U-可补充. 由定理充分性的条件知,H在G中X-ss-半置换的, 即存在T∈Xss(H). 若对G的任意素因子p,Op(G)=1. 由于X是G的可解正规子群, 所以X=1. 设H为q群,Q∈Sylr(G)且Tr∈Sylr(T), 其中(r,q)=1. 从而存在g∈G,使得Q=Trg. 因为H≤NG(X)=G, 所以Tg∈Xss(H). 从而HQ=QH, 即H在G中s-半置换的. 设A是G的一个极小次正规子群. 如果|A|=s,s为素数, 则A≤Os(G), 矛盾. 从而A为单群且非交换. 因为H在G中s-半置换的, 所以对A中任意元素a,HQa=QaH. 因为(|HQa:H|,|HQa:Qa|)=1, 所以由文 [12],HQa∩A=(A∩H)(A∩Qa)= (A∩H)(A∩Q)a为A的子群. 因为(A∩H)(A∩Q)a可解且A不可解, 所以(A∩H)(A∩Q)a是A的真子群. 由引理4 得A非单群. 这一矛盾说明存在G的一个素因子p,使得Op(G)≠1. 由N的唯一极小正规性,N≤Op(G). 从而(3)成立.
(4) 最后的矛盾.
设P∈Sylp(E). 由(3)知,N≤P且P非循环. 设H为包含在N中P的极小正规子群. 所以|H|=p且H≤N≤E. 下面断言:H正规于G. 设T为H在G中的一个补充子群, 即G=HT. 从而N=N∩HT=H(N∩T)且G=NT. 又因为N正规于G且N为交换群, 所以N∩T正规于G. 由N的极小正规性得N∩T=1或者N∩T=N. 若N∩T=1, 则H=H(N∩T)=N正规于G. 若N∩T=N,则N≤T. 故T=G非超可解群. 由定理充分性的条件,T∈Xss(H). 设Q∈Sylq(T), 其中q≠p. 则存在x∈X,使得HQx=QxH. 因为N为初等交换群, 所以H正规于N. 因为N正规于G, 所以H是G的次正规子群. 由于Qx∈Sylq(G), 所以HQx为{p,q}群. 故H∈Sylp(HQx)且H也是HQx的次正规子群. 从而H正规于HQx. 即Qx≤NG(H). 又因为H正规于P, 所以H正规于G.因为N是G的极小正规子群, 所以N=H为p-阶子群. 由(1)G/N∈F及引理2得G∈F. 这一最后的矛盾表明极小反例不成立, 从而定理充分性成立.
注1定理1充分性条件对幂零群不成立. 如G=S3为三次对称群,E=(<123>)为G的3阶循环子群. 则G/E为2阶循环群,当然是幂零群.E仅有一个循环Sylow 3-子群, 于是G满足定理1充分性条件, 但G不是幂零群.
注2定理1充分性条件“4 阶循环子群”不能去掉. 如G=[E]K, 其中E=
推论1群G为超可解的充分必要条件是存在G一个正规子群E,使得G/E∈U且E的每个非循环Sylow子群的极小子群和4阶循环子群在G中U-可补充.
推论2设F是包含U的饱和群系,X是G的可解正规子群. 如果G有正规子群E,使得G/E∈F且E的每个Sylow子群的极小子群和4阶循环子群在G中X-ss-半置换的. 则G∈F.
推论3[3]设F是包含U的饱和群系. 如果G有正规子群E,使得G/E∈F且E的每个极小子群和4阶循环子群在G中s-半置换的. 则G∈F.
推论4[9]设E是G的超可解上根. 如果E的每个极小子群和4 阶循环子群在G中s-半置换的, 则G是超可解的.
定理2设F是包含U的饱和群系,X是G的可解正规子群. 如果G有可解正规子群E,使得G/E∈F且F(E)的每个极小子群和4阶循环子群在G中X-ss-半置换的. 则G∈F.
证明假设结论不成立. 设G为极小阶反例. 令P是F(E)的任一Sylowp-子群, 其中p是F(E)的素因子. 分以下步骤来完成定理的证明.
(1)P∩Φ(G)=1.
设N=P∩Φ(G)≠1. 显然(G/N)/(E/N)≅G/E∈F. 由文[14]可知F(E/N)=F(E)/N. 设T/N是F(E/N)的极小子群或者4阶循环子群. 则对应的存在F(E)的一个极小子群或4阶循环子群H, 使得T=HN. 由定理的条件及引理1(2)得L/N在G/N中XN/N-ss-半置换的. 由G的极小选择,G/N∈F. 因为N≤Φ(G), 所以G∈F. 这一矛盾说明P∩Φ(G)=1.
(2)P=N1×N2×…×Nt, 其中Ni(i=1,2,…,t)为G的素数阶极小正规子群.
因为P正规于G且P∩Φ(G)=1, 所以由引理3知P=N1×N2×…×Nt, 其中Ni(i=1,2,…,t)为G的极小正规子群. 设H为包含在Ni中P的极小正规子群, 则|H|=p. 由定理的条件知H在G中X-ss-半置换的, 即存在T∈Xss(H).设Q∈Sylq(T), 其中q≠p. 则存在x∈X,使得HQx=QxH. 因为Ni为初等交换群, 所以H正规于Ni. 因为Ni正规于G, 所以H是G的次正规子群. 由于Qx∈Sylq(G), 所以HQx为{p,q}群. 故H∈Sylp(HQx)且H也是HQx的次正规子群. 从而H正规于HQx. 即Qx≤NG(H). 又因为H正规于P, 所以H正规于G. 因为Ni.是G的极小正规子群, 所以Ni=H为p-阶循环群.
(3) 最后的矛盾.
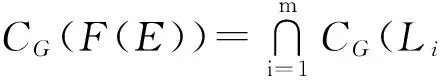
G/CG(Li)=NG(Li)/CG(Li)≅Aut(Li).
因为Li(i=1,2,…,m)为素数阶循环群, 所以Aut(Li)为交换群. 从而G/CG(Li)∈F. 因为G/CG(F(E))同构于G/CG(L1)×G/CG(L2) ×…×G/CG(Lm)的一个子群, 所以G/CG(F(E))∈F.
因为G/CE(F(E))=G/CG(F(E)∩E)同构于G/CG(F(E))×G/E的一个子群, 所以G/CE(F(E))∈F. 而E可解, 故由文[12]得CE(F(E))≤F(E). 从而F(E)=CE(F(E)). 因此G/F(E)∈F. 由定理1知,G∈F. 这一最后的矛盾表明极小反例不成立, 从而定理成立.
推论5[3]设F是包含U的饱和群系. 如果G有可解正规子群E,使得G/E∈F且F(E)的每个极小子群和4阶循环子群在G中s-半置换的, 则G∈F.
[1]KENGE O H. Sylow-Gruppen and subnormaleiler end licher Gruppen[J]. Math Z, 1962, 78 (1): 205-221.
[2]陈重穆. 关于Srinivasan的一个定理[J]. 西南师范大学学报(自然科学版), 1987, 12 (1):1-4.
[3]张勤海, 王丽芳.s-半置换子群对群结构的影响[J]. 数学学报, 2005, 48 (1): 81-88.
[4]GUO W B, SHUM K P, SKIBA A N.X-permutable maximal subgroups of Sylow subgroups of finite groups[J]. Ukrain Matem J, 2006, 58 (10): 1471-1480.
[5]GUO W B, SHUM K P, SKIBA A N.X-semipermutable maximal subgroups of finite groups[J]. J Alegebra, 2007, 315 (1): 31-41.
[6]HAO L P, WANG Y.Two sufficient conditions for supersolubility of finite groups[J]. J Xu Zhou Normal Univ (Natural Science Edition), 2008, 3 (26): 14-18.
[7]WANG L F, ZHANG Q H. Influence ofs-semipermutability subgroups of prime power order on the structure of finite groups[J]. J Math Res Exp, 2005, 25 (3): 423-428.
[8]SHAALAN A. The influnece ofs-quasinormality of some subgroups on the stucture of a finite group[J]. Acta Math Hungar, 1990, 56: 287-293.
[9]WANG K R. Minimal subgroups and structure of finite groups[J]. J Sichuan Normal Univ (Natural Science Edition), 2006, 6 (29): 631-634.
[10]祝明. 有限群的X-ss-半置换子群[D]. 重庆: 西南大学数学与统计学院, 2011.
[11]GUO W B. OnF-supplemtned subgroups of finite groups[J]. Mauscripta Math, 2008, 127: 139-150.
[12]GUO W B. The theory of class of groups[M]. Bejing: Science Press-Kluwer Academic Publishers, 2000.
[13]KEGEL O H. Produkte nilpotenter Gruppen[J]. Arch Math, 1961, 12: 90-93.
[14]HUPPERT B. Endliche Gruppen I[M]. Berlin:Springer, 1967.
(责任编辑朱夜明)
The influence of the X-ss-semipermutability on the structure of finite groups
XIE Fengyan1, MAO Yuemei2
(1. School of Civil Engineering and Architecture, Anyang University, Anyang 455000, China;2. School Mathematics and Computer Science, Datong university, Datong 037009,China)
LetGbe a finite group andXa nonempty subset ofG.AsubgroupHofGis said to beX-ss-semipermutable ifHhas a supplementTinG, such thatHisX-permutable with every Sylowp-subgroups ofTwith (p,|H|)=1. TheX-ss-semipermutability of minimal subgroups was used to characterize the structure of finite groups. Some known results were unified and generalized.
minimal subgroup; supersolvable group;X-ss-semipermutable subgroup; saturated formation
10.3969/j.issn.1000-2162.2016.05.003
2015-11-10
国家自然科学基金资助项目(11401264); 河南省高等学校重点科研基金资助项目(15A110048)
谢凤艳(1984-),女,河南开封人,安阳学院讲师, 硕士.
O152.1
A
1000-2162(2016)05-0014-04

