基于2008—2015年实测数据的苏通大桥风速风向联合分布分析
王 浩 徐梓栋 陶天友 姚程渊 李爱群
(东南大学混凝土及预应力混凝土结构教育部重点实验室, 南京 210096)
基于2008—2015年实测数据的苏通大桥风速风向联合分布分析
王浩 徐梓栋 陶天友 姚程渊 李爱群
(东南大学混凝土及预应力混凝土结构教育部重点实验室, 南京 210096)
为充分掌握苏通大桥桥址区基本风速,基于大桥结构健康监测系统(SHMS)运行7年(2008年1月至2015年3月)的实测数据开展了桥址区风速风向联合分布分析.利用安装在主梁跨中上游、跨中下游和南塔塔顶的3个风速仪采集的数据,以1个月作为基本抽样时间间隔,采用阶段极值法抽取极值样本.在进行Gumbel,Frechet和Weibull分布函数的参数估计后,根据风向频度函数得到桥址区风速风向联合分布,据此对桥址区10,50及100年重现期的极值风速进行了推算.结果表明,Weibull概型风速风向联合分布函数较Gumbel和Frechet概型更为合适,考虑风向影响的基本风速使结构抗风设计更加接近实际情况,而苏通大桥抗风设计时所采用的基本风速偏于保守.
苏通大桥;结构健康监测系统;风速风向联合分布;基本风速;数理统计方法
风对结构的作用是空间性的,因地理、环境等因素的影响,不同方向上风特性存在差异.随着土木工程结构向长大化方向发展,越来越多的工程结构在空间不同方向上的尺度表现出明显差异,这将导致结构在不同方向上的风敏感性存在显著差异.因此,以往抗风设计中对空间不同方向存在尺度差异的工程结构均采用基本风速进行设计是不尽合理的.考虑特定场地空间尺度存在差异的工程结构所受风荷载时,有必要考虑风向的影响,因此需构建相应的风速风向联合分布函数,从而可以得到一定重现期下各风向对应的基本风速.
为有效掌握某地区不同方向上的基本风速分布,最有效的方法是依托结构所在场地实测数据对风速风向联合分布进行分析.Justus等[1]、Garcia等[2]基于实测风数据开展了不同联合分布概型的拟合与检验,结果表明Weibull分布和对数正态分布与实测数据的拟合效果均良好,而Weibull概型拟合结果更优.Gupta[3]基于印度多个地区实测数据进行了Weibull概型参数估计,结果表明不同地区、不同高度分布参数拟合结果差异明显.杨咏昕等[4]提出了基于最小二乘法原理考虑风速风向联合分布的平均风统计分析方法,分析了上海地区的平均风,说明了考虑风速风向联合分布的必要性.张春涛等[5]基于重庆日极值风建立了风速条件概率密度混合模型,同时结合风向概率密度提出了风向风速离散-连续混合模型.陈隽等[6]基于统一的风速风向边缘分布极值概型提出了一种7参数风速风向联合分布解析表达式,同时给出了风向区间的建议划分法.范文亮等[7]基于重庆日极值风样本并利用乘法定理建立了风速风向离散-连续混合分布模型,分别拟合得到风速风向的混合分布模型.王浩等[8]基于苏通大桥结构健康监测系统(structural health monitoring system, SHMS)为期4年的监测数据分析了桥址区风速风向联合分布概型,依据数理统计方法推算了4个部位不同重现期的极值风速;Feng等[9]基于给定方位区间中的实测风速数据,拟合得到不同方位区间内Weibull分布函数的参数,通过在各方位区间之间引入插值函数得到了风速风向联合分布连续函数.很明显,现有风速风向联合分布研究主要采用气象站资料进行,因此针对大跨度桥梁等大型重要工程结构物所在场地、基于长期监测风环境数据的风速风向联合分布研究具有重要意义.
本文基于苏通大桥SHMS长达7年(2008年1月至2015年3月)的实测风特性数据,依据阶段极值法抽取极值样本进行极值分布函数参数拟合,通过引入风向频度函数得到了不同风向上极值风速分布,据此预测了10,50及100年重现期下桥址区基本风速,并与已有研究结果及规范建议值进行了对比分析,以期为桥址区风速风向联合分布的进一步分析提供基础,同时为大跨度桥梁风致振动精细化分析提供参考.
1 苏通大桥风速仪布置简介
苏通大桥为东南沿海的交通枢纽工程之一,为了有效地对桥址区的风环境进行监测和评估,在大桥主跨共安装了4个风速仪(见图1).其中,离地高度约76.9 m的大桥跨中上、下游侧各布置一个风速仪(FS4和FS4′);离地高度约306 m的大桥南、北桥塔顶部各布置一个风速仪(FS6和FS2).设定正北方向为实测风向角的零度,规定顺时针旋转为正.

图1 苏通大桥风速仪布置图(单位:m)
2 风速风向联合分布
2.1风速风向联合分布概率模型
本文以风向频度函数与各风向分布函数的乘积来建立反应风速风向共同作用的联合分布概率模型[4,10-11],函数表达式为
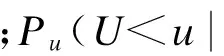
2.2极值风速样本的抽样和整理
为确保样本数据的代表性,基于阶段极值法[4-5]取1个月作为基本抽样时间间隔.取10 min作为基本时距,考虑苏通大桥结构对称性,两塔顶风速仪仅选取了南塔监测结果进行分析.故对FS4,FS4′及FS6三个风速仪实测数据进行极值风速样本抽样,选取2 m/s作为风速区间间隔,统计得到不同测点各风速区间在16个风向上发生的频度,结果见图2.
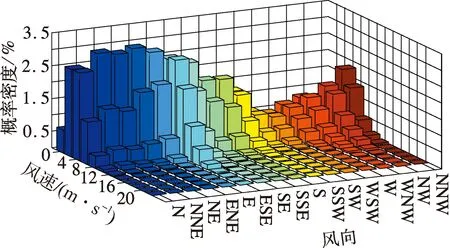
(a) FS4
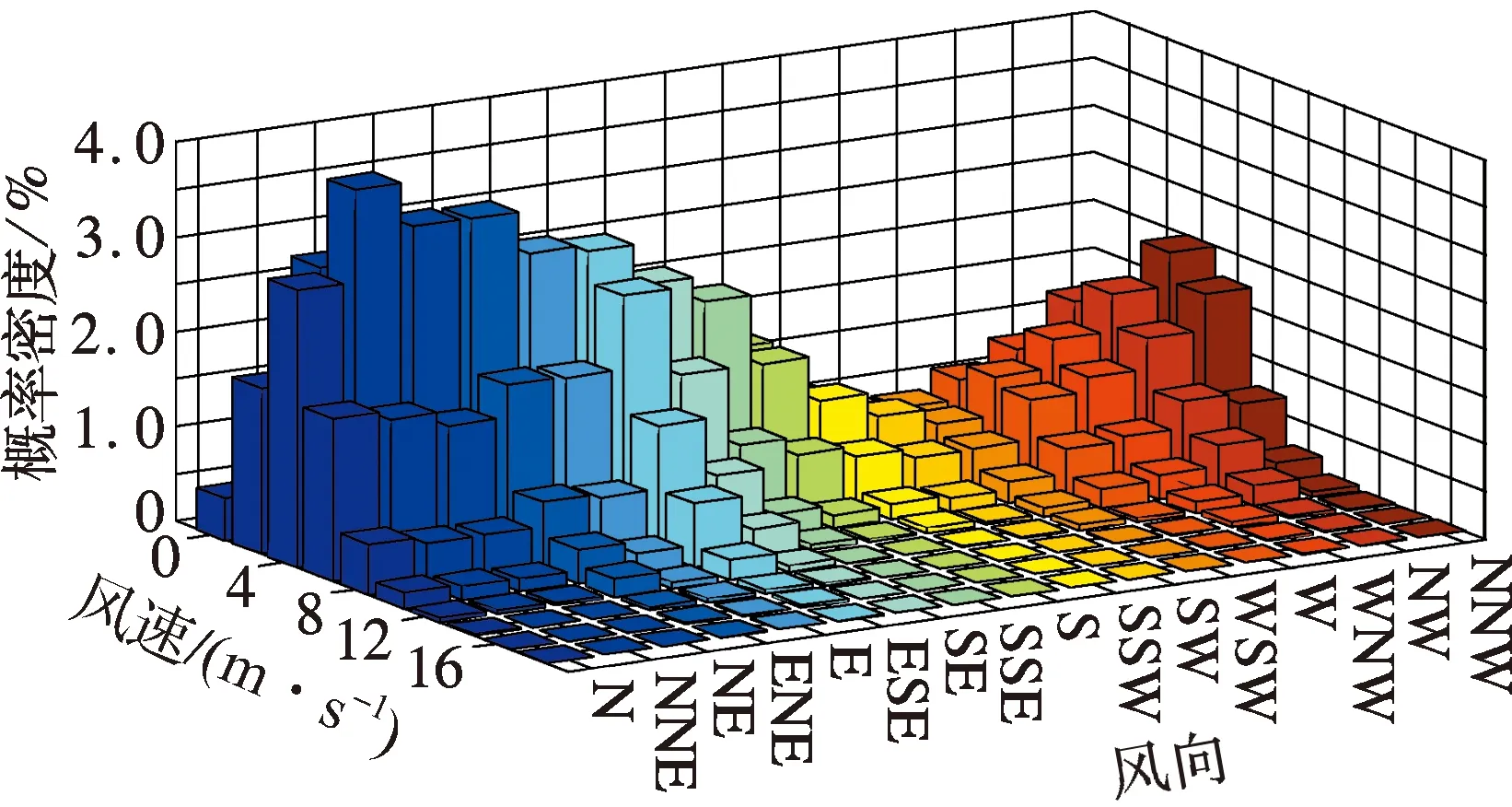
(b) FS4′
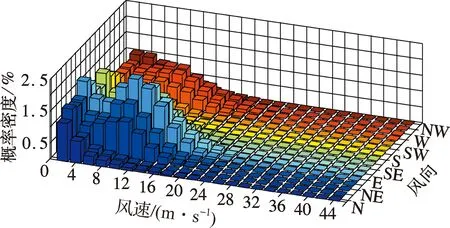
(c) FS6
2.3联合分布概型的检验与拟合
依据阶段极值抽样法得到各方向不同风速区间的发生频数统计数据,进行风速风向联合分布的
极值风速分布概型拟合,拟合时遵循如下2条基本假定[6,10]:
① 同一地点、不同方向的平均风速服从同一类型的极值分布概型,并由各方向极值样本来拟合最优极值分布概型;
② 同一测点、不同方向上极值风速的分布概型拟合参数是相互独立的,只由本方向上的样本数据来确定.
针对广义越界分布概型在风工程领域中的3种极值分布函数,可以得到3种风速风向联合分布概率模型[12-14].
1) Gumbel概率分布函数
(2)
2) Frechet概率分布函数
(3)
3) Weibull概率分布函数
式中,参数a,b和γ均为风向θ的函数.
针对某一风速仪测点,基于各风向上极值风速样本,本文采用最小二乘法拟合以上分布函数的参数.虽然拟合函数本身并非线性形式,但通过变换可化为线性模型,从而简化分析.
1) Gumbel分布函数线性模型
u=b-aln[-lnP(U≤u)]
(5)
2) Frechet分布函数线性模型
ln[-lnP(U≤u)]=-γ(lnu-lna)
(6)
3) Weibull分布函数线性模型
ln[-lnP(U>u)]=γ(lnu-lna)
(7)
基于全体极值样本拟合得到3类极值分布函数的参数解,采用概率曲线相关系数法计算得到拟合函数与样本数据间的相关系数r,从而描述模型与实测数据的匹配程度,r越接近1,则模型的拟合程度越优[15].基于总体样本的风速风向联合分布函数参数拟合结果见表1.

表1 基于总体样本的风速风向联合分布函数参数拟合
由表1可以看出,3类分布函数与极值样本均具有较好的相关性,而极值样本与Weibull分布更为相近,与文献[8]结果一致.针对各风速仪测点处16个风向上极值风速样本数据对Weibull风速风向联合分布函数参数进行估计,参数拟合结果见表2.
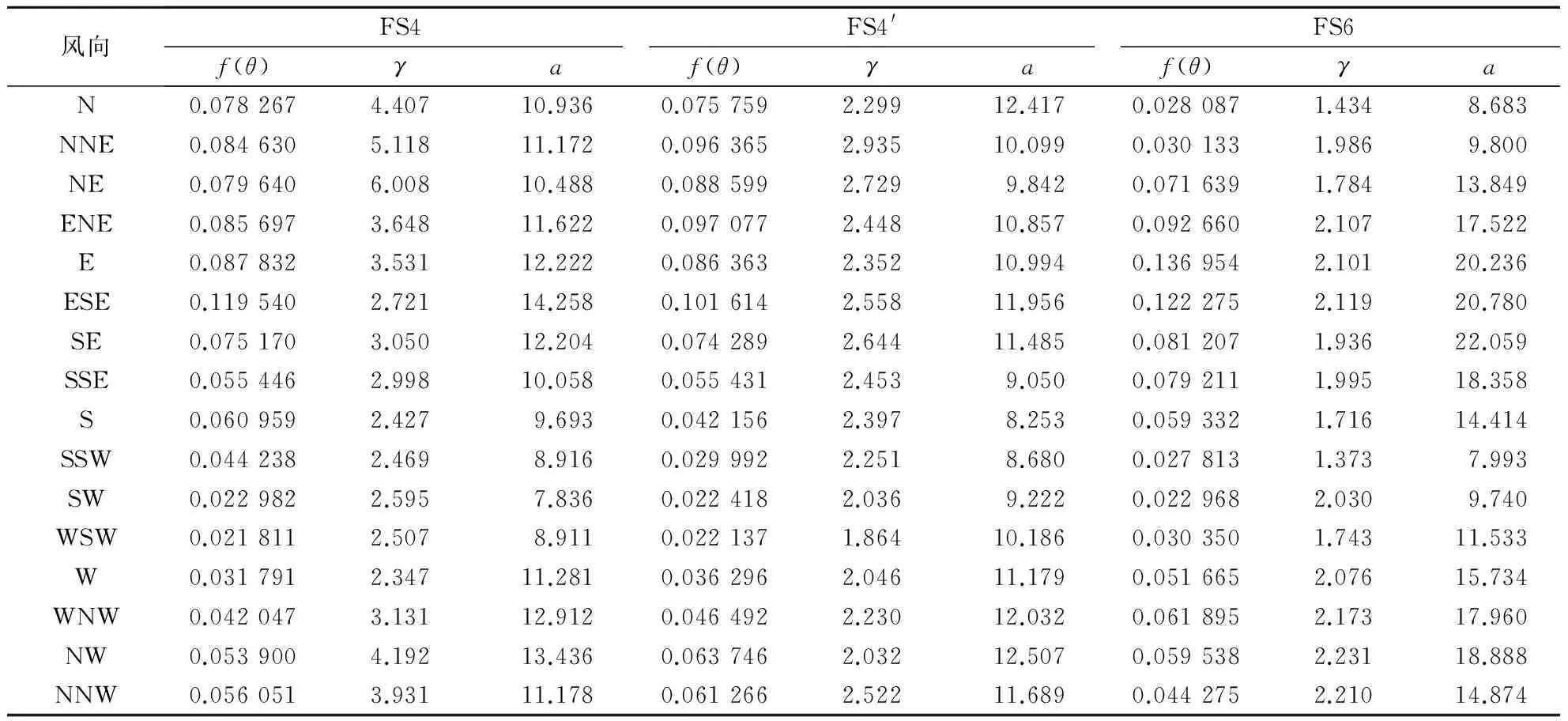
表2 风速仪测点处Weibull分布参数估计结果
2.4基于风速风向联合分布的基本风速预测
取桥址区基本风速重现期M,则桥址区极值风速超越基本风速的概率为1/M.假设给定一年的K次强风样本,则样本极值风速与基本风速间的概率存在如下关系:
(8)

(9)
由于本文采用阶段极值抽样法,并取一个月作为基本时间间隔,因此K取值为12.根据式(9)并结合式(4),可得Weibull极值分布概型对应于基本风速重现期为M的基本风速估计函数[8]为
UJ=a(θ){ln[MKf(θ)]}1/γ(θ)
(10)
对所得极值风速样本进行极值分布函数参数拟合,基于整体样本统计得到各个方位风向频度函数f(θ),根据式(10),分别取基本风速重现期10,50和100年,对苏通大桥FS4,FS4′和FS6风速仪测点16个方位上基本风速进行估计.为直观反映各方位上基本风速分布情况,分别绘制苏通大桥不同测点处基于Weibull极值概型的基本风速玫瑰图(见图3).为方便与传统不考虑风速风向联合分布所得基本风速进行比较,表3列出了FS4,FS4′和FS6风速仪10,50及100年全方位基本风速估计值.
由图3及表3计算结果可知:
1) 在西北与东南方向上基本风速较其他方位大,这与桥址区常年盛行的冬季强北风与夏季东南季风密切相关,同时FS4与FS4′实测数据间存在一定关联性,表明苏通大桥风速仪实测数据具有可靠性.
2) 大多数情况下,考虑风向影响所得基本风速值比不考虑风向影响所得基本风速值偏小.然而,某些方向上基本风速大小关系也存在特例,即考虑风向的基本风速大于忽略风向影响的基本风速.如FS4测点,100年重现期,ESE方向基本风速值为25.69 m/s,大于忽略风向影响的全方位基本风速值21.93 m/s;FS4′测点,100年重现期,N与NW方向上基本风速值分别为23.91和25.74 m/s,大于忽略风向影响的全方位基本风速值23.79 m/s.说明忽略风向影响的基本风速值在多数方位上较考虑风向影响的基本风速值偏大,设计偏安全,而考虑风向影响后,在桥址区主导风向上的基本风速值则有可能偏大,这与文献[8]的分析结果一致.
3) FS4与FS4′测点处基本风速估计结果存在明显差异,这与桥梁结构自身对流场所产生的干扰有关.因此对结构进行风速风向监测的过程中,在对风速仪进行安装布设时需格外注意,以减少结构自身干扰对实测风环境数据的影响.

(a) FS4

(b) FS4′
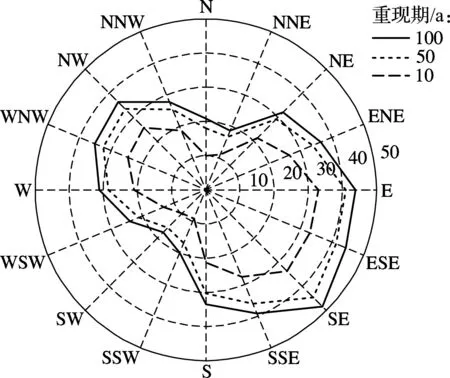
(c) FS6

m/s
2.5苏通大桥基本风速估计值与规范建议值对比
根据我国《公路桥梁抗风设计规范》(JTGT D60-01—2004),100年重现期下,苏通大桥桥址区7.1 m高度处设计基本风速为28.6 m/s.规范同时假定大气边界层内风速沿铅直高度的分布服从幂指数律,即
(11)
式中,h1与h2为计算点距地面高度;Uh1与Uh2为h1与h2高度处风速;α为考虑场地表面粗糙度的无量纲幂指数,桥址区α取为0.12.经计算得苏通大桥主梁跨中与塔顶设计基本风速分别为38.06与44.93 m/s[8].
与基本风速估计结果进行对比可知,对作为主要受风构件的大桥主梁而言,无论是否考虑风向影响,设计采用的基本风速值均大于基于实测数据所得的估计值,大桥抗风设计所取的基本风速均偏于安全,与文献[8]分析结果一致.
3 结论
1) 基本风速在西北、东南方向较其他方位更大,与桥址区常年盛行冬季强北风与夏季东南台风密切相关,从侧面说明了实测数据的可靠性.
2) 本文相关研究结论与文献[8]基于4年监测数据、抽样时间间隔取为4 d时所得结论基本一致,使得2次分析结果的可靠性得到了进一步的相互验证.
3) 就苏通大桥桥址区而言,基于Weibull概型的桥址区风速风向联合分布函数较Gumbel及Frechet概型更为合适.
4) 考虑风向影响的基本风速值比不考虑风向影响时偏小,与文献[8,15]结论一致.因此,考虑风向影响的基本风速使得结构抗风设计更接近实际情况.
5) 无论是否考虑风向影响,设计采用基本风速值均大于基于实测数据的估计值,说明苏通大桥抗风设计所考虑的基本风速偏于安全.
References)
[1]Justus C G, Hargraves W R, Yalcin A. National assessment of potential output from wind powered generators[J].JournalofAppliedMeteorology, 1976, 15(7): 673-678. DOI:10.1175/1520-0450(1976)015<0673:naopof>2.0.co;2.
[2]Garcia A, Torres J L, Prieto E, et al. Fitting wind speed distributions: A case study[J].SolarEnergy, 1998, 62(2): 139-144. DOI:10.1016/s0038-092x(97)00116-3.
[3]Gupta B K. Weibull parameters for annual and monthly wind speed distributions for five locations in India[J].SolarEnergy, 1986, 37(6): 469-471. DOI:10.1016/0038-092x(86)90039-3.
[4]杨咏昕,葛耀君,项海帆.风速风向联合分布的平均风统计分析[J].结构工程师,2002,18(3):29-36,46. DOI:10.3969/j.issn.1005-0159.2002.03.006.
Yang Yongxin, Ge Yaojun, Xiang Haifan. Statistical analysis of wind speed based on the joint distribution of wind speed and wind Direction[J].StructuralEngineers, 2002, 18(3): 29-36,46. DOI:10.3969/j.issn.1005-0159.2002.03.006. (in Chinese)
[5]张春涛,李正良,范文亮,等.考虑风向风速联合分布的输电塔线体系风振疲劳研究[J].工程力学,2013,30(3):315-322.
Zhang Chuntao, Li Zhengliang, Fan Wenliang, et al. Study on wind-induced fatigue of transmission tower-line coupled system considering the joint distribution of wind speed and wind direction[J].EngineeringMechanics, 2013, 30(3): 315-322. (in Chinese)
[6]陈隽,徐骏飞.风速风向联合概率密度分布的一种经验函数模型[J].防灾减灾工程学报,2014,34(1):13-19.
Chen Juan, Xu Junfei. An empirical joint probability density function of wind speed and direction[J].JournalofDisasterPreventionandMitigationEngineering, 2014, 34(1): 13-19. (in Chinese)
[7]范文亮,李正良,张培.风速风向的联合概率结构建模[J].土木工程学报,2012,45(4):81-90.
Fan Wenliang, Li Zhengliang, Zhang Pei. Modeling of the joint probability structure of wind direction and speed[J].ChinaCivilEngineeringJournal, 2012, 45(4): 81-90. (in Chinese)
[8]王浩,王龙花,樊星辰,等.基于健康监测的苏通大桥风速风向联合分布研究[J].桥梁建设,2013,43(5):55-61.
Wang Hao, Wang Longhua, Fan Xingchen, et al. Study of joint distribution of wind speed and direction of Sutong bridge based on SHMS[J].BridgeConstruction, 2013, 43(5): 55-61. (in Chinese)
[9]Feng J, Shen W Z. Modeling wind for wind farm layout optimization using joint distribution of wind speed and wind direction[J].Energies, 2015, 8(4): 3075-3092.
[10]王钦华,顾明.风速风向联合分布对结构风致疲劳寿命可靠性的影响[J].振动与冲击,2009,25(6):98-103.
Wang Qinhua, Gu Ming. Influence of joint distribution of wind speed and wind direction on wind-induced fatigue life reliability[J].JournalofVibrationandShock, 2009, 25(6): 98-103. (in Chinese)
[11]James P. Statistical inference using extreme order statistics[J].TheAnnalsofStatistics, 1975, 3(1): 119-131.
[12]段忠东,欧进萍,周道成.极值风速的最优概率模型[J].土木工程学报,2002,35(5):11-16. DOI:10.3321/j.issn:1000-131X.2002.05.003.
Duan Zhongdong, Ou Jinping, Zhou Daocheng. The optimal probabilistic distribution for extreme wind speed[J].ChinaCivilEngineeringJournal, 2002, 35(5): 11-16. DOI:10.3321/j.issn:1000-131X.2002.05.003. (in Chinese)
[13]Jose A C, Penelope R, Celia B. A joint probability density function of wind speed and direction for wind energy analysis[J].EnergyConversionandManagement, 2008, 49(6): 1309-1320.
[14]董学武,张宇峰,徐宏,等.苏通大桥结构健康监测及安全评价系统简介[J].桥梁建设,2006,36(4):71-73,81. DOI:10.3969/j.issn.1003-4722.2006.04.021.
Dong Xuewu, Zhang Yufeng, Xu Hong, et al. Structural health monitoring and safety evaluation system for Sutong bridge[J].BridgeConstruction, 2006, 36(4): 71-73, 81. DOI:10.3969/j.issn.1003-4722.2006.04.021. (in Chinese)
[15]Simiu E, Filliben J J. Wind direction effects on cladding and structural loads[J].EngineeringStructures,1982, 4(3): 181-186.
Analysis on joint distribution of wind speed and direction on Sutong Bridge based on measured data from 2008 to 2015
Wang Hao Xu Zidong Tao Tianyou Yao Chengyuan Li Aiqun
(Key Laboratory of Concrete and Prestressed Concrete Structures of Ministry of Education, Southeast University, Nanjing 210096, China)
In order to fully grasp the basic wind speed at Sutong Bridge site, the joint distribution of the wind speeds and directions on the bridge was analyzed based on the seven-year (Jan. 2008 to Mar. 2015) data recorded by the structural health monitoring system (SHMS). By using the data recorded by three anemometers installed on the upstream and downstream sides of the mid-span of the main girder and at the south pylon top, an extreme value sample was selected by the stage extreme value sampling method using one month as the basic interval. After the parameters of Gumbel, Frechet, and Weibull distribution functions were estimated, the joint distribution of the wind speeds and the wind directions at the bridge site was obtained according to the wind direction frequency function. The extreme wind speeds in 10, 50, and 100-year recurrence intervals at the bridge site were calculated. Results show that the Weibull distribution function is more appropriate than that of Gumbel distribution and the Frechet distribution for analyzing the joint distribution of the wind speeds and directions at the bridge site. Considering the effects of the wind direction on the estimation of the basic wind speed makes structural wind-resistant design more practical, thus the basic wind speed during the design of Sutong Bridge is conservative.
Sutong Bridge; structural health monitoring system; joint distribution of wind speed and wind direction; basic wind speed; mathematical statistic method
10.3969/j.issn.1001-0505.2016.04.027
2015-11-05.作者简介: 王浩(1980—),男,博士,研究员,博士生导师,wanghao1980@seu.edu.cn.
国家重点基础研究发展计划(973计划)资助项目(2015CB060000)、国家自然科学基金资助项目(51378111,51438002).
10.3969/j.issn.1001-0505.2016.04.027.
U448.27;V321
A
1001-0505(2016)04-0836-06
引用本文: 王浩,徐梓栋,陶天友,等.基于2008—2015年实测数据的苏通大桥风速风向联合分布分析[J].东南大学学报(自然科学版),2016,46(4):836-841.

