两类特殊图的邻点强可区别E-全染色

顾忠栋，强会英，魏邦魁

（兰州交通大学 数理与软件工程学院，甘肃 兰州730070）

两类特殊图的邻点强可区别E-全染色

顾忠栋，强会英*，魏邦魁

（兰州交通大学 数理与软件工程学院，甘肃 兰州730070）

对简单图G（V，E），存在一个正整数k，使得映射f：V（G）∪E（G）→｛1，2，…，k｝，如果∀uv∈E（G），有f（u）≠f（v），f（u）≠f（uv）且C（u）≠C（v），其中C（u）=｛f（u）｝∪｛f（uv），f（v）|uv∈E（G），v∈V（G）｝，则称f是图G的邻点强可区别E-全染色，且称最小的数k为图G的邻点强可区别E-全色数。在此基础上应用构造染色法研究了图Fm×Fn、M（Pn2）的邻点强可区别E-全染色，并得出了其邻点强可区别E-全色数。

笛卡尔积图；k方图；邻点强可区别E-全染色；邻点强可区别E-全色数

随着计算机的飞速发展，信息化和数字化技术的不断进步，许多实际问题的数学模型使离散型结构上的数字化技术得到了更多人的关注，图的染色理论［1］作为离散数学的一个重要的组成部分，自然得到了快速发展，因此，受到了国际数学界与工程界越来越广泛的重视。Noga Alon在2002年数学国际大会上作了“离散数学方法与挑战”的大会报告后，图的染色成为一个很活跃、很新颖的研究领域。1993年，A.C.Burris在他的博士论文中提到了点可区别正常边染色（也称强边染色）的概念［2］，此后P.N.Balister等人［3］对该问题进行了深入的讨论，许多研究成果都在国际权威杂志上刊出。在无线通讯网络中，为了防止网络中不同的长点之间信号频率的共振，必须保证不同站点之间拥有不同的通讯频率，为了解决无线传感器网络中相邻点通信冲突问题及交通运输中危险品运输的配送调度安全问题等，张忠辅教授首次提出了邻点可区别正常边染色［4］的概念，这一问题与点可区别边染色的研究具有相同的难度，因此，国内外专家对此问题作了大量研究。2004年，张忠辅教授在邻点可区别正常边染色的基础上提出了邻点可区别全染色［5］的概念。2007年，张忠辅教授又提出了邻点强可区别全染色的概念［6］。2010年，程辉等在邻点强可区别的基础上提出了邻点强可区别EI-全染色［7］和邻点强可区别VI-全染色的概念［8］。笔者在此基础上得到了两类特殊图的邻点强可区别E-全染色。下面给出相关的定义。

1　基本概念

定义1［6］设图G是阶数至少为2的连通图，映射f：V（G）∪E（G）→｛1，2，…，k｝，其中k为正整数，如果f满足：

（1）对任意的uv∈E（G），f（u）≠f（v），f（u）≠f（uv），f（v）≠f（uv）；

（2）对任意的uv，uw∈E（G），u≠w，f（uv）≠f（uw）；

（3）对任意的uv∈E（G），u≠v，C（u）≠C（v）。

则称f为图G的k-邻点强可区别全染色，简记为k-AVSDTC，又称

为G的邻点强可区别全色数，这里C（u）=｛f（u）｝∪｛f（uv），f（v）|uv∈E（G），v∈V（G）｝。

定义2设图G是阶数至少为2的连通图，映射f：V（G）∪E（G）→｛1，2，…，k｝，其中k为自然数，如果f满足：

（1）对任意的uv∈E（G），u≠v，f（u）≠f（v），f（u）≠f（uv）；

（2）对任意的uv∈E（G），u≠v，C（u）≠C（v）。

则称f为G的k－邻点强可区别E－全染色，简记为k－E－AVSDTC，又称

为图的邻点强可区别E－全色数。这里C（u）＝｛f（u）｝∪｛f（uv），f（v）|uv∈E（G），v∈V（G）｝。

由图的邻点强可区别全染色和图的邻点强可区别E-全染色的概念，下面引理成立：

定义3［9］设m阶扇Fm和n阶扇Fn，即Fm与Fn构成的笛卡尔直积图Fm×Fn的定义为

定义4［10］对图G＝（V，E），和自然数k，若V（Gk）＝V（G），E（Gk）＝E（G）∪｛uv|d（u，v）=k｝，则称图Gk为图G的k方图。

定义5［11］对图G（V，E），M（G）称为图G的Mycielski图，其中：

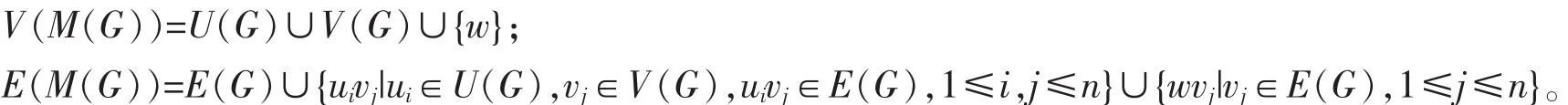
文中未加说明的术语可参考文献［12-13］。

2　主要结论

定理1对于扇和扇的笛卡尔积图Fm×Fn（m≥3，n≥3），则有

此时对f的色集合如下：

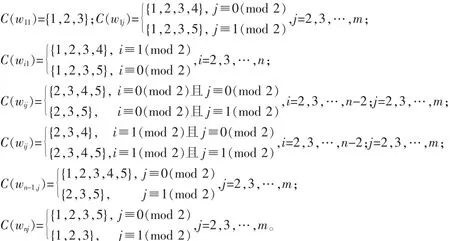
显然，对∀uv∈E（G），有C（u）≠C（v），故结论成立。

定理2设Pn是n个点的路（n≥4）则，有

证明设图 M（Pn2）的顶点集和边集分别为 V（M（Pn2））＝｛ui|i=1，2，…，n｝∪｛vj|j=1，2，…，n｝∪｛w｝，E（M（Pn2））＝E（Pn2）∪｛uivj|uivj∈E（Pn2），1≤i，j≤n｝∪｛wvj|1≤j≤n｝。易知 χ（M（Pn2））＝3，由引理 1可知先证明否则若事实上因图存在三圈，易证故下面给出图M（Pn2）的一个5-E-AVSDTC染色法，令f如下：

当i＝3时，f（u3vj）＝5；当i≡2（mod 3）时，f（uivj）＝5，j=1，2，…，n；

此时对f色集合如下：

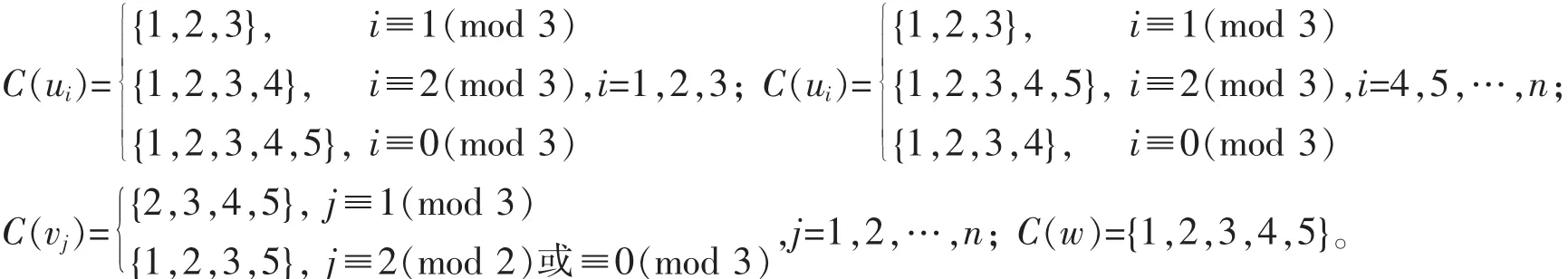
显然，对∀uv∈M（Pn2），有C（u）≠C（v）。结论成立。

［1］BONDY J A，MARTY U S R.Graph Theory with Application［M］.New York：The Macmillan Press Ltd，1976.

［2］BURRIS A C，SCHELP R H.Vertex-distinguishing proper edge-coloring［J］.J of Graph Theory，1997，26（2）：73-82.

［3］BALISTER P N，PIORDAN O M，SCHELP R H.Vertex-distinguishing edge coloring of graph［J］.Graph Throry，2003，42（2）：95-109.

［4］ZHANG Zhongfu，LIU Linzhong，WANG Jianfang.Adjacent strong edge-coloring of graph［J］.Applied Mathematic Letter，2002，15（5）：623-626.

［5］ZHANG Zhongfu，CHEN Xiangen，LI Jingwen，et al.On adjacent vertex-distinguishing total coloring of graphs［J］.Science in China：Ser A Mathmatics，2005，48（3）：289-299.

［6］张忠辅，程辉，姚兵，等.图的邻点强可区别全染色［J］.中国科学（A辑：数学），2007，37（9）：1073-1082.

［7］CHENG Hui，WANG Zhiyong.Adjacent vertex strongly distinguishing EI-total coloring of graphs［J］.Shandong Univ Nat Sci，2010（3）：289-299.

［8］程辉，谢雁.图的邻点强可区别VI-全染色［J］.兰州大学学报，2010，46（6）：97-101.

［9］王倩，田双亮.几类笛卡尔直积图的邻点可区别全染色［J］.苏州科技学院学报（自然科学版），2010，27（4）：15-17.

［10］FAVARON O，LI H，SCHELP R H.Strong edge coloring of graphs［J］.Discret Mathematics，1996，1（3）：103-109.

［11］孔令峰，苏文龙，罗海鹏，等.pn2的Mycielski图的邻点强边色数和邻点可区别全染色［J］.广西科学，2008，15（1）：4-6.

［12］强会英，王洪申.图的邻点强可区别全色数的一个上界［J］.数学进展，2013，42（6）：801-805.

［13］马刚，张忠辅.路与轮连图的邻强边色数［J］.苏州科技学院学报（自然科学版），2007，24（2）：1-4.

责任编辑：谢金春

On the adaject vertex strongly distinguishing E-total coloring of two special graphs

GU Zhongdong，QIANG Huiying，WEI Bangkui
（College of Mathematics，Physics and Software Engineering，Lanzhou Jiaotong University，Lanzhou 730070，China）

Let G（V，E）be a simple graph，k be a positive integer，f is a mapping from V（G）∪E（G）to｛1，2，…，k｝，then f is called the adgacent vertex strongly distinguishing E-total coloring of G and the minimum number of k is called the adjacent vertex strongly distinguishing E-total chromatic of G，if∀uv∈E（G）f（u）≠f（v），f（u）≠f（uv），∀uv∈E（G），C（u）≠C（v）.Based on this，this paper studied the adjacent vertex strongly distinguishing E-total coloring of graph of Fm×Fnand M（pn2）with the structure staining method.And the adjacent vertex strongly distinguishing E-total chromatic numbers of both graphs were obtained thereby.

Cartesian graph；k-square graph；adjacent vertex strongly distinguishing E-total coloring；adjacent vertex strongly distinguishing E-total chromatic number

O157.5MR（2000）Subject Classification：05C15；05C22；05C40

A

1672-0687（2016）03-0018-04

2016-01-16

国家自然科学基金资助项目（61262045）

顾忠栋（1990-），男，甘肃武威人，硕士研究生，研究方向：图论与组合优化。*通信联系人：强会英（1968-），女，甘肃白银人，教授，硕士生导师，E-mail：qhy2005ww@126.com。