深入浅出分析刚体摩擦力

姚黄涛　潘梦萍　冯 杰

(上海师范大学物理系　上海　200235)



深入浅出分析刚体摩擦力

姚黄涛潘梦萍冯 杰

(上海师范大学物理系上海200235)

以刚体在不同条件下运动状态为例，详细分析了刚体所受3种不同摩擦力的产生机制和效果．对比了实际物体与理想刚体的区别，并讨论了滚动摩擦的本质，最后对伽利略的斜面实验进行了“理想条件”的探讨．

刚体摩擦力滚动

在中学物理教学中，摩擦力一直是重点和难点，要想教会学生摩擦力的定性分析和定量运算，教师就要对摩擦力的概念和原理掌握得很好．当刚体涉及摩擦力时，往往使得问题变得复杂一些，譬如大学物理教程中刚体的摩擦力分析，这往往牵扯到很多的概念.

下面从5个方面来详细讨论刚体所受摩擦力，以便对力学中刚体摩擦力的教学提供参考．

1　斜面上刚体无滑滚动

刚体力学中，我们常常会碰到求解刚性球体做无滑滚动时的摩擦力，比较典型的是在斜面上的刚性小球的运动，如图1所示．

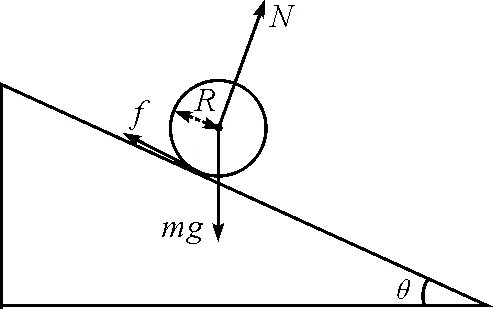
图1　斜面上的球体

根据球体做无滑滚动的条件和刚体对质心的转动定理，可以得出下列方程

其中I为转动惯量，aC为质心加速度，α为角加速度．

由式(1)、(2)得

(4)

设小球沿斜面滚下了距离s后下降了高度H，质心速度达到vC，滚动角速度为ω，则

(5)

平动动能

(6)

转动动能

(7)

总动能

Ek总=Ek平+Ek转=mgH=W重

(8)

以上计算表明刚体做无滑滚动时，相对于斜面参考系，此摩擦力不做功，为静摩擦力．

其一，因为存在这一静摩擦力，才使得刚体从斜面做无滑滚动滚落下来．重力对刚体所做的正功W重等于刚体总动能(平动动能与转动动能之和)的增加量．所以重力势能全部转化为平动动能与转动动能；

其二，此静摩擦力充当了桥梁的作用，使得重力势能可以一部分转化为转动动能，如果不存在此静摩擦力，刚体不会转动，只会滑下斜面，总动能完全是平动动能．

由式(2)、(3)、(4)我们可以得到静摩擦力f静的表达式

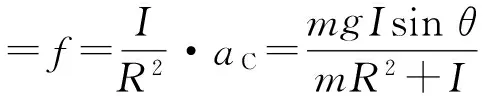
(9)

2　水平面上刚体无滑滚动

根据式(9)我们可以发现，当斜面倾角θ等于零度时f静=0，即当斜面变成水平面后，除了重力、刚体与斜面之间的弹力外不考虑外界施加的力，静摩擦力为零．换句话说就是静摩擦力不存在．这可以分两种情况讨论：

第一种情况是刚体静止于水平面上，此时刚体当然不会受到摩擦力的作用，因为重力和水平面对刚体的支持力正好平衡．

为了证明此种情况下刚体与水平面之间不存在摩擦力，我们再分为两种情况讨论，即假设摩擦力存在，分别为f左和f右(由于是刚体，不存在弹性形变，所以刚体与水平面的摩擦力只能沿公切面方向而平行于水平面)．

图2

如果存在向左的摩擦力f左，则vC就要减小，刚体要滚得慢了．Mf左使得刚体相对于质心的角速度ω增大，刚体要滚得快了，两个结果相矛盾，所以不存在f左．

如果存在向右的摩擦力f右，则vC就要增大，刚体要滚得快了．但质心的角速度ω却是减小，刚体要滚得慢．这种情况同样不会发生，所以不存在f右．

综上，刚体在上述情况下沿水平面做无滑滚动时，不存在静摩擦力．当刚体小球在水平面上达到上述的无滑滚动状态时，小球不受任何摩擦力的作用(在这一模型中，我们不考虑微观分子之间的相互作用)，如图2(b)所示，小球将保持其运动状态永远运动下去．

3　水平面上刚体有滑滚动

以上我们考虑了刚体处在水平面上做无滑滚动静摩擦力不存在的这一运动状态．那么，刚体如何达到这样的一种状态呢？

我们仍分两种情况讨论．

其一，刚体静止于水平面，在某一时刻受到作用于质心的力F，在F的作用下沿水平面向右加速滚动，显然此时刚体与水平面的接触点处的地面对刚体必然施加一向右的静摩擦力f，此f对质心的力矩使刚体产生顺时针转动的角加速度，我们可以方便求出f，α，aC的大小．当F撤去的时候，刚体受力情况就达到了图2所示的状态，不存在静摩擦力．即当力F撤离的瞬间，静摩擦力同时也消失了．此后刚体将一直以恒定速度滚动下去，即使刚体与水平面之间是粗糙的．

其二，刚体以平动速度vC，相对质心的角速度为ω=0这一运动状态施放在粗糙的刚性水平面上．如图3(a)所示，刚性小球放在传送带上与传送带一起向右以速度为vC运动，并且小球相对传送带静止，我们所要考虑的是小球离开传送带接触水平面后的运动状态的变化，即分析此种情况下刚体运动状态是如何变化到图3(b)所示的状态的．

图3

刚体刚接触水平面的瞬间，刚体与地面的接触点P的速度应为刚体的平动速度vC0．假如在这一瞬间刚体就完成了从只有平动到无滑滚动的这一状态的转变，那么P点相对于质心的转动线速度就必须在Δt时间内增加到vC0．

由刚体转动的动量矩定理

MΔt=ΔL=L末-L初

得

(10)

根据假设，Δt很短，短到几乎是一瞬间，即Δt→0,所以f→∞．因而除非刚体与水平面的结构如图4所示，使得f是一个冲力，否则静摩擦力不可能达到碰撞级别的效果．因而刚体与水平面接触时必然发生滑动，此摩擦力为滑动摩擦力．

图4　刚性齿轮结构

通过以上分析，我们可以定性地描述刚球接触水平面后的运动状态的变化过程．一开始刚球做有滑滚动，在滑动摩擦力的作用下，刚球平动速度减小而转动角速度在增加．当平动速度正好等于刚球边缘上P点的转动线速度时，刚体开始做无滑滚动，摩擦力消失．下面是定量计算：

如图3(b)所示，设μ与f动为钢球与水平面间的动摩擦因数和滑动摩擦力，则

f动=μmg=maC⟹aC=μg

球质心的平动速度为

vC=vC0-μgt

(11)

又

μmgR=Iα

取球体的转动惯量

(12)

所以

(13)

则接触点P相对于钢球质心的线速度

(14)

当vC=vP时，钢球达到无滑滚动的条件，钢球与水平面间不发生滑动，此时钢球处于图2(b)所示的状态，即不存在摩擦力．

由式(11)、(14)得

(15)

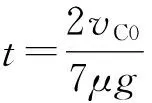
(16)

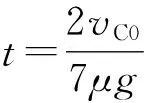
(17)

则钢球边缘在这段时间内滚动的弧度为

(18)

所以钢球与水平面之间的相对滑动距离为

(19)

因而滑动摩擦力做功产生的热量为

(20)

(21)

将式(15)代入上式，得

即

W损=Q

由上面的计算我们可以发现，从能量转化的角度计算的热量值与滑动摩擦力做功的值相等，所以证实了此摩擦力的确是滑动摩擦力．

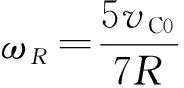
4　形变物体的滚动

运用刚体模型，我们得出了刚体在水平面上滚动时不存在静摩擦力的结论，刚体会一直滚动下去．显然这一结论与我们日常生活中的经验不符，在水平面上推动圆柱形的滚子，如果不继续推动它，滚子不会永远运动下去，而会慢慢停下来[1]．一般人们会说这是摩擦力的作用，但往往不会明确指出这究竟是什么摩擦力．

刚体是忽略一切形变的理想模型，实际物体显然不满足刚体这一条件，即实际物体受到力的作用总会或多或少地发生形变，形变较小的物体较硬，形变较大的物体较软．我们考虑较硬的圆柱体置于较软的水平面上，如图5(a)所示．当滚子以一定的初始速度vC在水平发生向左的滚动时，接触面因受力不均匀而向左端隆起，从而导致地面对滚子的弹力N改变为如图5(b)所示的N′，这个力N′不过滚子的质心，因而产生了阻碍滚子滚动的力矩M′，同时N′水平向右的分量保证了滚子的平动速度减小．为了研究方便，将N′正交分解为竖直方向的FN和水平方向的Ff，Ff大致与滚子与地面的公切面平行，而FN近似与公切面垂直，可看作地面对滚子的弹性支持力．

图5

将力FN平移至滚子的质心O，并附加一力偶矩，如图5(c)所示，作用于质心O点的力FN与重力平衡，而附加力偶矩起阻碍滚动的作用，称滚动摩擦力偶矩[1],将其大小记为M滚，用δ表示O点到FN的力臂如图5(d)所示，则

M滚=FNδ

至此我们可以看到阻碍滚子滚动正是这个滚动摩擦力偶矩的作用．现在，我们通过刚体平动与转动的规律来计算N′的水平分力Ff．

Ff=maC

由于是无滑滚动

aC=Rα

M滚-FfR=Iα

(25)

对于圆柱体滚子

代入上式，得

其中

(26)

我们可以发现式(26)具有摩擦力的表达形式．

尽管Ff是形变地面对滚子支持力的水平分力，但我们可以将Ff看成是滚子在水平面上滚动时受到的滚动摩擦力，μ′称为滚动摩擦因子．根据

我们不难发现当滚子的半径越大，滚动摩擦力越小．路面越硬，形变越小，δ就越小，所以滚动摩擦力也就越小．因此在松软的路面上骑车比在水泥路面上费力．火车采用钢轨作为轨道也是减小滚动摩擦的原因．许多机器采用的滚动轴承，其滚轴中有许多球体或柱体在内外环间滚动，在制造上要求滚动体和环都有很高的硬度，其目的在于减小滚动摩擦．由于δ≪R，查阅相关技术手册[1]后发现μ′的数量级处在10-2，比滑动摩擦因子小一个数量级．这就是大家常说的滚动摩擦比滑动摩擦小的原因．至此有一点值得一提，上面讨论的滚动摩擦力Ff不是像滑动摩擦力一样实际存在的摩擦力，而是为了方便比较而将N′的水平分力根据效果而命名的，本质上还是弹力．

当我们讨论滚动时，要知道滚动摩擦这一效果是由滚动摩擦力偶矩M摩，而不是Ff作用而产生的．因为存在形变，所以研究对象不再是刚体这一理想模型．

5　伽利略的理想斜面实验

伽利略通过科学推理认为，如果一切接触面都是光滑的，一个钢球从斜面的某一高度A处静止滚下，由于只受重力，没有阻力产生能量损耗，那么它必定达到另一斜面的同一高度C，如果把斜面放平缓一些，也会出现同样的情况，如D，E的高度，如果斜面变成水平面，则钢珠找不到同一高度而会一直保持一种运动状态，永不停止的运动下去，如图6所示[2]．

图6　伽利略理想斜面实验

对于这个理想实验，存在值得讨论的地方．如果一切接触面都是光滑的，那么根据前文的分析，钢球是不可能滚动下来的，而只会沿斜面向下滑．要使钢球做无滑滚动滚下斜面，那么必然存在斜面对钢球沿斜面向上的静摩擦力，既然存在摩擦力，那么伽利略的斜面实验还是理想的吗？

一方面，根据前文的分析，要使钢球从斜面上滚动下来，就必须存在斜面对钢球的摩擦力．同时，这个摩擦力必须是静摩擦力，因为只有静摩擦力才能保证钢球的重力势能改变量等于钢球平动动能和转动动能之和，使得钢球能回到另一斜面的同一高度．另一方面，要使钢球在水平轨道上保持恒定速度永远运动下去，根据前文的分析，钢球必须不受到滚动摩擦力偶矩的作用，那么钢球与轨道必须不发生形变，即刚体与轨道必须是理想的刚体模型．

因此，我们认为伽利略的理想斜面实验中的“理想”二字的描述不是忽略所有摩擦力的理想状态，而是钢球与轨道必须是理想刚体，且钢球与轨道之间是纯静摩擦力这一理想状态．

当然了，伽利略在设计这一理想实验时的上述不足，并不一定是伽利略的疏忽．这也许是后人在叙述这一理想实验时外加的，也许是伽利略的知识局限性所引起的，因为在当时关于摩擦的知识还比较缺乏[2]．所以我们必须站在历史的角度看待这一理想实验，丝毫不否认其在物理学发展中的巨大作用．

1漆安慎，杜婵英.力学(第二版).北京：高等教育出版社，2005.240～242

2陶洪.物理实验论.南宁：广西教育出版社，1996.49～50

2016-04-17)