基于氮化铝的1 310 nm波段可调DFB激光器的设计

陈凯文，胡芳仁，王 斐

（南京邮电大学光电工程学院，南京 210046）

基于氮化铝的1 310 nm波段可调DFB激光器的设计

陈凯文，胡芳仁，王 斐

（南京邮电大学光电工程学院，南京 210046）

依据严格耦合波理论和介质平板波导理论，基于MEMS（微机电系统）技术，利用周期可调谐的布拉格光栅设计了一种基于氮化铝的波长可调DFB-LD（分布反馈激光器）。采用梳齿状驱动器驱动光栅动态调节，并利用有限元软件COMSOL对其在1 310 nm波段进行模拟仿真。对激光器电场模式图进行分析，确定了DFB-LD的光栅结构参数。分析表明，激光器输出波长与光栅周期呈线性关系，且一个光栅周期对应多个不同的光栅高度值。在小于模式截止光栅高度的情况下呈20 nm周期性分布。依据光栅周期和激射波长的关系，提出了制作1 290～1 330 nm波段可调激光器的可能性。

氮化铝；分布反馈激光器；波长可调；微机电系统

0　引 言

随着通信技术的不断发展，人们对带宽的要求也日益提高，大容量、高速率以及高频谱效率的光通信网络逐渐成为下一代通信网络的主流［1］。波长可调谐激光器在简化DWDM（密集波分复用）系统光源配置的同时也大幅度提升了光通信系统的性价比［2］。目前，波长可调DFB-LD（分布反馈激光器）已成为光通信系统至关重要的一部分。另外，随着MEMS（微机电系统）技术的发展，可调谐的Ga N（氮化镓）激光器及滤波器已有报道，但是基于Al N（氮化铝）材料集成制备波长可调谐DFB-LD的研究较少［3］。

本文依据严格耦合波理论和介质平板波导理论［4］，通过数值计算，建立了基于Al N的可调DFBLD二维模型［5］。分析研究了激光器在不同光栅结构下的输出特性以及输出波长与光栅周期的对应关系，为实现波长可调谐DFB-LD的制造提供了理论基础及数据参考。

1　结构与设计原理

布拉格散射必须满足的基本条件为

式中，φi、φs分别表示入射角和散射角；m为布拉格散射的阶数；Λ为光栅周期；neff为光栅材料的等效折射率；λ0为对应的波长。为使激光器稳定单模输出，通常我们取入射角度φ=90°，阶数m=1。

根据耦合波理论和麦克斯韦方程组，波动方程可简化为

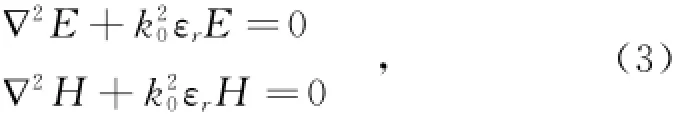
式中，k0为真空波数。考虑到仿真时采用TE波（水平极化波）入射，因此本文仅对TE波单模传输特性进行研究。布拉格光栅中的亥姆霍兹方程为

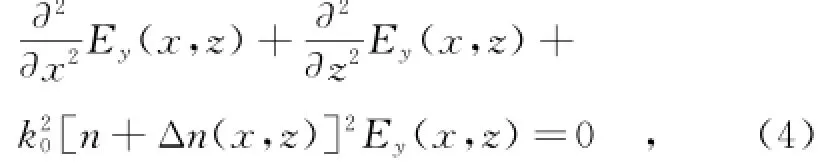
式中，Δn（x，z）为沿z轴折射率的周期变化，且Δn（x，z）=neff+Δn cos（2β0z），β0=mπ/Λ为布拉格波数。

图1所示为DFB-LD光栅结构分布反馈示意图。在耦合波分析中，光栅虽然会产生无穷对正向波和反向波，但只需考虑满足β=β0时强度最大的一对波（分别用a（z）、b（z）表示），所得耦合波方程组为

式中，α为阈值增益；κ为耦合系数；δ为相位失谐因子，且有，其中，β= k0neff。由式（5）可知，相向波耦合并增益加强，两者叠加形成DFB-LD的单模输出。

图1 DFB-LD光栅结构分布反馈示意图

图2所示为DFB-LD波导光栅结构图，光波沿水平方向传输，图中，d为光栅宽度，H为光栅高度，Λ为光栅波导周期，Ht为波导结构的等效增益层厚度。由图可知，波导结构的等效折射率为

式中，Γ=d/Λ为光栅占空比，nair=1。

图2　DFB-LD波导光栅结构图

结合式（2）与式（6）可得激光器设计波长、光栅周期和光栅宽度的关系表达式为

图3所示为MEMS静电梳状驱动光栅的结构图。在梳状驱动上加驱动电压，产生的驱动位移带动光栅结构改变光栅周期，从而改变激光器的输出特性。

图3　MEMS静电梳状驱动光栅结构图

2　参数分析及特性研究

采用COMSOL软件对Al N基DFB-LD谐振腔建立二维模型，研究谐振腔的参数变化对激光器输出特性的影响，并结合MEMS技术，采用梳齿状静电驱动光栅实现周期可调，从而为实现波长可调DFB-LD提供可能性。本文取Γ=0.5，λ0= 1 310 nm，由式（7）可计算出光栅周期和对应的光栅宽度分别为390.65和195.33 nm，取有源层厚度为40 nm，利用COMSOL软件的参数化扫描功能，可以扫描出最优化的光栅高度，并可对激光器输出波长的单色性进行分析。结果表明，Λ=390 n m、d=195 nm时电场模式最好，谐振效果最明显。

图4所示为全局最大电场振幅随光栅高度的变化图。由图可见，当光栅高度为265.9nm时，电场模振幅达到108量级。图5所示为光栅全局总电能图。由图可知，光栅高度为265.9 nm时，总电能高达4.0×10-6J，谐振效果十分明显。

图4 光栅电场振幅图

图6所示为有源层厚度为40 nm时不同的光栅高度与全局总电能图。由图可看出，总电能峰值可达10-6数量级，在光栅高度为265.9 nm处，全局总电能为4.2×10-6J，谐振效果明显。同时可以观察到电能峰值与所对应的光栅高度近似成20 nm周期性变化，稳定的电场模式在270 nm处消失，这是由于光栅高度达到该值后谐振腔内产生了模式截止，致使稳定的电场模式消失。

图5　光栅全局总电能图

图6 光栅高度与全局总电能图

图7所示为光栅高度H=265.9 nm时不同周期下的电场模式图。由图可知，在全局结构中，周期为390 nm条件下的电场模振幅值远远高于其他周期条件下的电场模振幅值，这说明其他周期所对应的激光模式得到了很好的抑制。图8所示为不同周期对应电场能量分布图。由图8（b）可以看出，光栅周期为390 nm时，中心区域电场振幅最大，峰值高达6.002 9×108V/m，往两侧急剧减小并趋近于零，表明谐振腔内形成了稳定的电场模式。对比图 8（a）、（b）和（c）可知，谐振腔结构内电场模式分布趋于分散，说明周期的改变对谐振效果的影响较为明显，因此可通过改变光栅周期来抑制其他激光模式从而实现激光单模输出。

图7　不同周期对应一维电场模式图

图8　不同周期对应电场能量分布图

考虑到波长可调，本文研究了不同输出波长与对应光栅周期的关系。设定波长范围为1 290～1 330 nm、光栅宽度d=106 nm，对光栅周期进行参数化扫描。图9所示为激光器设计波长与光栅周期关系图。由图可以看出，波长与光栅周期近似呈线性关系，由拟合曲线可得关系式：Γ=142.223-0.406 33λ，与上文所得结论一致，拟合度高达0.999 7。通过适当调节电压改变驱动器驱动位移从而改变谐振腔光栅周期，便可以实现激光器输出波长的动态可调。

图9　激光器设计波长与光栅周期关系图

3　结束语

依据耦合波理论和严格的介质平板波理论，基于MEMS技术设计了一种Al N波长可调DFBLD，并对激光器的输出特性进行分析，提出了通过线性改变光栅周期来实现激光输出波长的可调，确定了1 290～1 330 nm之间波长与周期的对应关系，为Al N波长可调DFB-LD的结构设计及制备提供了理论依据。

［1］ GAUDINO R，CURRI V，BOSCO G，et al.On the use of DFB lasers for coherent PON［C］//OFC 2012， New York，US：IEEE，2012：1-3.

［2］ Bruce E.Tunable lasers［J］.IEEE Spectrum，2002，39（2）：35-39.

［3］ KNOPP K J，VAKHSHOORI D，WANG P D.High power MEMs-tunable vertical-cavity surface-emitting lasers［C］//LEOS 2001.Coper Mountain，CO，USA：IEEE，2001：31-32.

［4］ KOGELNIK H，SH ANK C K.Coupled-Wave Theory of Distributed Feedback Lasers［J］.Journal of Applied Physics，2008，43（5）：2327-2335.

［5］ Streifer WILLIAM，Scifres DONALD R，Burnham ROBERT D.Coupled wave analysis of DFB and DBR lasers［J］.IEEE Journal of Quantum Electronics，1977，13（4）：134-141.

Design and Analysis of the Wavelength-Tunable DFB Laser Based on Al N in 1 310 nm-Band

CHEN Kai-wen，HU Fang-ren，WANG Fei
（School of Optoelectronic Engineering，Nanjing University of Posts&Telecommunications，Nanjing 210046，China）

Based on the rigorous coupled-wave theory and medium slab waveguide theory，an Al N wavelength tunable distributed feedback laser is designed by Periodic tunable Bragg grating.The adjustable grating is actuated by comb-drive actuator according to the Micro-Electromechanical（MEMS）technology system and simulated by COMSOL software in 1 310 nm band. The parameters of the DFB laser grating structure are evaluated by analyzing the distribution of a two-dimensional electric mode.Also，the simulation results show that the lasing wavelength and grating period have similar linear relationships，which is consistent with the theoretical analysis.Moreover，one grating period corresponds to a number of different grating heights，and it demonstrates periodic distribution in a 20 nm range.Furthermore，according to the relationship between lasing wavelength and grating period，the possibility of making 1 290～1 330 nm-band tunable lasers is presented in this paper.

Al N；DFB-LD；wavelength-tunable；MEMS

TN248

A

1005-8788（2016）04-0031-03

10.13756/j.gtxyj.2016.04.010

2016-04-19

国家自然科学基金资助项目（61274121，61574080）

陈凯文（1992-），男，江苏南京人。硕士研究生，主要研究方向为微机电系统、光电子器件。