基于模糊双门限的高频地波雷达与AIS目标航迹关联方法

刘根旺，刘永信，纪永刚，王　超（.内蒙古大学电子信息工程学院，内蒙古　呼和浩特000；.国家海洋局第一海洋研究所，山东　青岛6606；3.国家海洋局航天科技集团公司海洋遥测工程技术研究中心，山东　青岛6606）

基于模糊双门限的高频地波雷达与AIS目标航迹关联方法

刘根旺1，2，刘永信1，纪永刚2，3，王超2
（1.内蒙古大学电子信息工程学院，内蒙古呼和浩特010021；2.国家海洋局第一海洋研究所，山东青岛266061；3.国家海洋局航天科技集团公司海洋遥测工程技术研究中心，山东青岛266061）

提出了一种基于模糊双门限的地波雷达与船只身份自动识别系统（auto matic identification system，AIS）目标航迹关联方法，该方法主要是利用模糊隶属度来描述两条航迹间的关联程度，并通过双门限检测来确定关联的航迹对。具体讨论分析了算法中展度、权重、调整因子等参数的选取原则，最后利用2011年10月31和2013年9月6日获取的两批实测地波雷达与AIS数据将本文方法与最近邻航迹关联算法做了对比，结果表明，此方法的关联率高于最近邻航迹关联算法，并且在航迹较为复杂情况下，提出的航迹关联算法具有更好的稳定性。

高频地波雷达；自动识别系统；航迹关联

网址：www.sys-ele.com

0 引 言

高频地波雷达（high frequency surface wave radar，H FS W R）与自动识别系统（auto matic identification system，AIS）是海上目标航迹跟踪探测的主要手段。其中，高频地波雷达可实时监测并跟踪区域内的船只目标，但无法提供目标的身份信息［1-2］；AIS能提供监视区域内的合作目标的动态和身份信息，但不能提供非合作目标的信息，且一旦船上的AIS关机，监视系统就失去了对船只的监视能力。这两种手段具有各自的优势和弱点，通过地波雷达和AIS目标航迹关联，一方面可以解决监视区域内的重复跟踪问题，提高跟踪效率；另一方面可以通过排除关联的合作目标而重点关注无身份的非合作目标［3］。

文献［4-8］相继开展了基于AIS数据的地波雷达舰船探测评价分析。文献［9-10］在地波雷达与AIS船只目标信息融合探测的研究中开展了点迹的关联。文献［11］首次提出了将AIS与地波雷达进行航迹融合的跟踪与关联算法，利用卡尔曼滤波计算了关联成本后，采用类似双门检测的方法判定关联后进行航迹融合，但该方法不能在无法对目标状态进行估计的系统中应用。总体来说，基于AIS的目标探测研究较多，但主要是作为验证手段，AIS的功能未得到充分利用。

本文通过开展地波雷达与AIS船只目标探测实验获取了实测数据；分析了两种手段的航迹数据的特点。论文给出了航迹关联算法的原理和流程，分析了关联方法中参数选取范围，最后通过实测数据，将本文中的方法与最近邻法做了对比分析。

1 航迹关联原理及流程

1.1 地波雷达与AIS航迹关联流程

地波雷达和AIS在进行航迹关联前，需要进行坐标变换与时间对准，实现二者在时空上的统一，然后再进行航迹关联，处理流程如图1所示。

图1 地波雷达与AIS航迹关联流程

AIS的经纬度信息通过坐标变换转换为与地波雷达一致的距离和方位信息，再将AIS的速度做径向投影变换，图2给出了统一后的点迹信息示意图。表示为

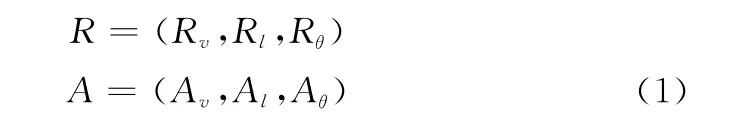
式中，Rv，Rl，Rθ表示地波雷达检测目标的径向速度、距离和方向；Av，Al，Aθ表示AIS报告的目标的径向速度、距离和方向。采用分段线性插值和外推法对AIS航迹进行时间插值，实现了与地波雷达的时间对准［12］。经过坐标转换和时间对准后的航迹数据就可以采用关联算法来进行航迹关联。

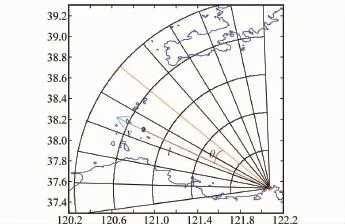
图2 目标点迹信息示意图

1.2 基于模糊双门限的地波雷达与AIS航迹关联算法

假设原始的地波雷达和AIS航迹数据经过坐标变换和时间对准后，得到了两组航迹集合

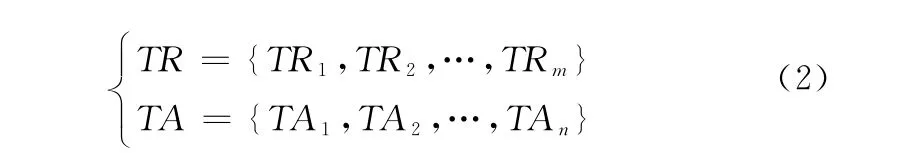
式中，TR表示地波雷达航迹集合，共有m条航迹；TA表示AIS航迹，共n条航迹。本文方法的原理是选取目标径向速度、距离、方向作为模糊因素，主要是利用模糊隶属度来描述两条航迹间的关联程度，并通过双门限检测来确定最终关联的航迹对。具体步骤如下。

1.2.1 模糊因素集的选取

选取两航迹信息的3个的特征信息作为模糊因素集。

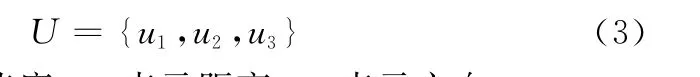
式中，u1表示径向速度；u2表示距离；u3表示方向。

1.2.2 隶属度函数的选择

根据模糊因素的特点，采用正态分布型隶属度函数：

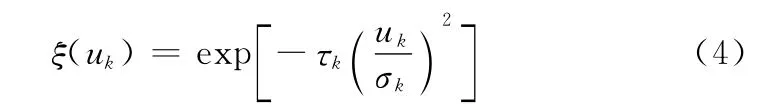
式中，ξ（uk）表示模糊因素集中第k个因素的隶属度函数；τk，uk，σk分别表示第k个模糊因素的调整因子、欧氏距离和展度。

计算模糊因素的欧氏距离。具体计算公式如下：

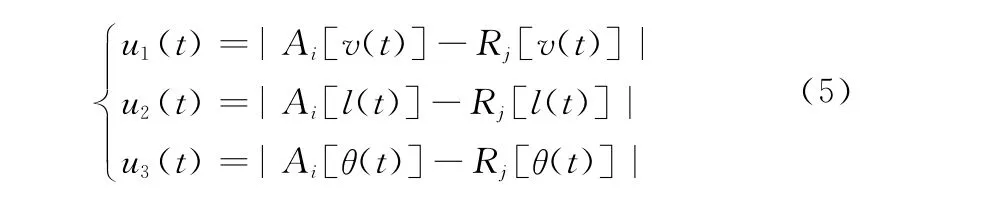
式中，Ai［v（t）］，Rj［v（t）］分别表示地波雷和AIS在t时刻测得的航速，朝向雷达基站行驶的为正，相反为负；Ai［l（t）］，Rj［l（t）］表示地波雷达和AIS在t时刻测得的目标距雷达基站的距离；Ai［θ（t）］，Rj［θ（t）］表示地波雷达和AIS在t时刻测得的目标相对于雷达主波束的角度。雷达主波束中心角度为北偏西50°，顺时针为正，逆时针为负。

1.2.3 计算模糊综合相似度

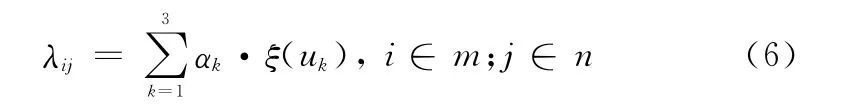
式中，λij表示第i条地波雷达航迹与第j条AIS航迹的综合相似度；αk表示权重；ξ（uk）表示第k个模糊因素隶属度函数值，共有m条地波雷达航迹，n条AIS航迹。地波雷达测速精度高的原因，在关联中航速应起主导作用，距离次之，航向影响最小。

1.2.4 航迹试验相关检验

对来自地波雷达的m条航迹和来自AIS的n条航迹进行计算，建立模糊相关矩阵。

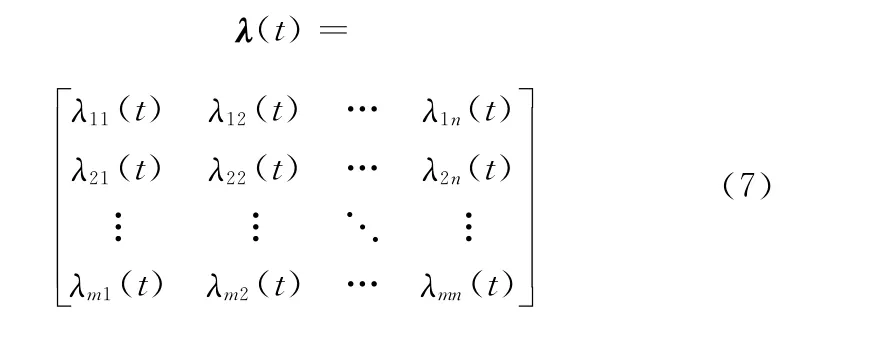
根据阈值法对航迹进行试验相关检验，步骤如下。

步骤1 选取阈值ε。

步骤2 在矩阵λ中查找最大元素max（λij），如果λij≥ε，则判定第i条地波雷达航迹与第j条AIS航迹在t时刻试验相关，记录下地波雷达的航迹编号和AIS的编号。从矩阵中划去λij所在的行和列，得到新的降阶模糊关联矩阵λ1，但原矩阵行列号保持不变。

步骤3 对λ1重复步骤2，得到λ2，λ3，…，λm，直到λm中所有元素均小于ε，则剩余元素所对应的行、列号所代表的航迹不相关。

1.2.5 双门限相关检测

单一时刻的关联只能说明当前时刻的关联性，而航迹是具有历史属性的，所以根据信号检测中双门限准则，取正整数R=10，I=8，在每次试验相关检验中如果试验关联成功，则有mij（l）=mij（l-1）+1（i∈m，j∈n），mij（l）定义为关联质量，（mij（0）=0）。如果在R次关联检验完成后，有

判定航迹i与j固定关联，后续不再进行检验［13］。

2 关联算法中的参数选取

在航迹关联中，参数的确定一般都采用工程的方法，需要进行大量的试验，以得到较为合理的结果［14］。本文航迹关联算法中涉及到αk，τk，σk，ε，R，I等共12个参数。

2.1 展度及调整因子选取

αk表示第k个因素的展度，一般的求法是航迹在。时刻的状态估计方差的对角元素的和，要想取得该值，需要在航迹实时生成中采用Kalman滤波得到。而在不能直接提供状态估计方差的系统中，αk可以用测量方差代替。本文统计了实际关联的航迹间径向速度、距离以及角度的误差分布，计算其误差的方差代替展度。

从图3中可以得到误差的波门范围分别为d V=0.8，d R=5，d A=5，3个特征信息的误差均值和方差列于表1。

表1 三维信息均值方差统计表

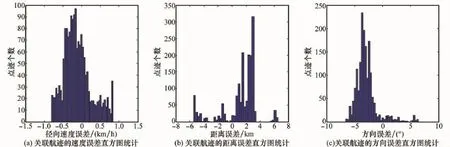
图3 三维误差信息直方图统计

上述中得到的方差可作为展度用与计算隶属度。实际运算中，将其取整以方便运算。取=0.4（k m/h）2；σ= 2.5 k m2；σ=2（°）2。

ε表示相关性，一般以0.5为界，大于等于0.5的表示相关，小于0.5则不相关。此处取ε=0.5。针对三维模糊因素集，根据式（4），可知三维隶属度要进行加权相加。若是取单一的隶属度，则权值为1即可。假设在目标刚落入门限内时，认为其可以关联，根据式（4），可以列出下列等式：

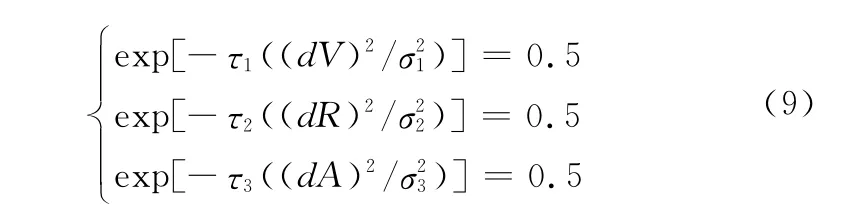
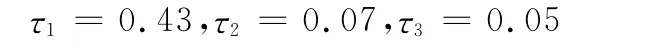
取整τ1=0.5，τ2=0.07，τ3=0.05。通过调整因子的使用，可以将不用数量级的特征信息调整到同一量级，使小数也能有较大的影响作用。

2.2 权值选取

计算综合模糊隶属度的时候，需要确定每个模糊因素的权重，权值按模糊因素的主导性来分配，在关联中起主导作用的径向速度分配权值较大，距离次之，方向最小［15］。3个权值应该满足

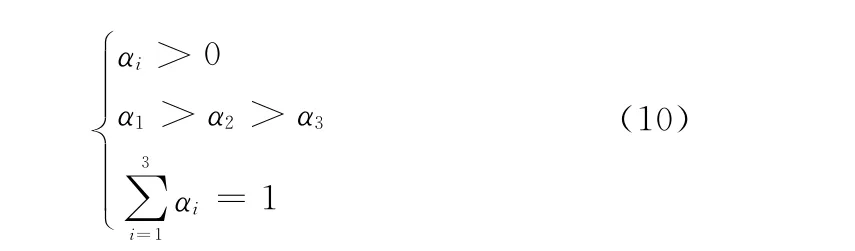
3个权值的选择可以用测量的相对误差的比例来初步确定。根据

式中，VT表示真实值；VM表示测量值；Ei表示相对误差。误差小则比例应该大，所以取其倒数，将3个比例按百分比计算，如下：

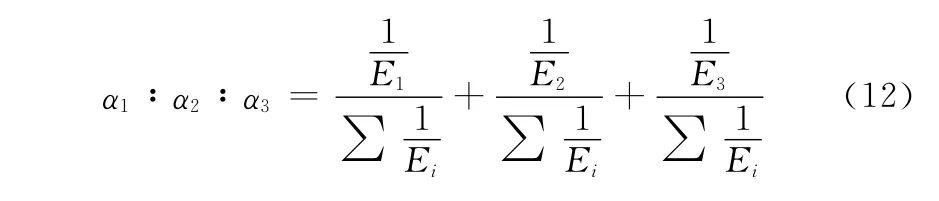
用地波雷达表示测量值，AIS表示真实值，经过筛选剔除奇点后，统计了关联航迹中的三维信息的相对误差，均值及方差。

经过统计分析，得到3个特征信息的相对误差的均值和方差如表2所示。

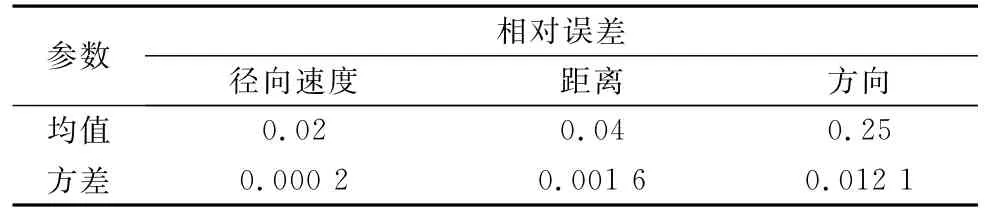
表2 相对误差统计表

将表中的均值代入式（4）～式（17）近似计算得到

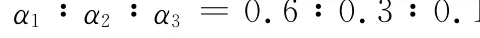
上述权值分配满足了式（10），在实际关联中也适用。另外采用定值仿真的方法，对于给定的单一因素关联隶属度，采用不同的权值组合计算综合模糊隶属度。权值组合如表3所示。

表3 权值组合表

对于单因素分别为（0.9，0.5，0.5）、（0.5，0.9，0.5）、（0.5，0.5，0.9）以及（0.9，0.7，0.5）、（0.9，0.5，0.7）、（0.7，0.9，0.5）、（0.7，0.5，0.9）、（0.5，0.9，0.7）、（0.5，0.7，0.9）的情况进行计算，得到的综合隶属度曲线如图4所示。

图4 综合隶属度曲线

对于模糊隶属度集合为U（0.9，0.5，0.5）的情况，满足条件的权值组合有（0.5，0.3，0.2）（0.5，0.4，0.1）（0.6，0.3，0.1）（0.7，0.2，0.1），其中，区分度较好的是（0.6，0.3，0.1）。

对于模糊隶属度集合为U（0.9，0.7，0.5）的情况，满足这个条件的权值组合有（0.5，0.3，0.2）、（0.6，0.3，0.1）、（0.7，0.2，0.1）其中（0.6，0.3，0.1）的区分度最好。

综合两种方法，最后确定为

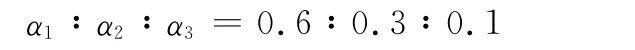
2.3 双门限参数选取

双门限参数R与I的选择一般根据实际情况来确定。实际情况既要考虑船只目标的运动特性，也要考虑处理中对计算机的占用需求，初步可设定为10/8组合，允许在航迹推进中出现2个奇异值或者是突变值，这样不会因为一两个点的差异而影响整个航迹关联，而且设定为10/8也不需要占用计算机太多内存。最后，所有参数如表4所示。

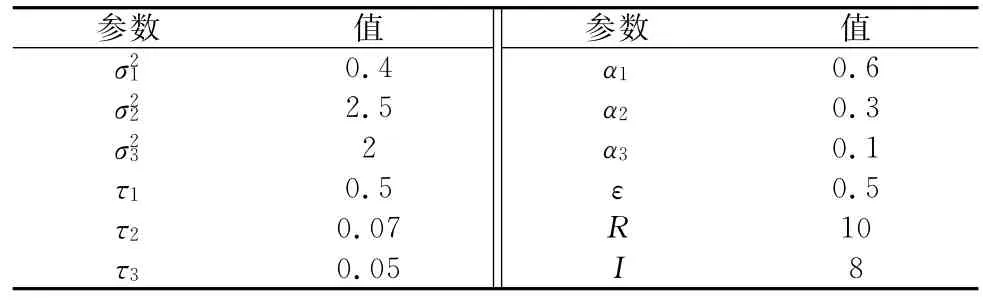
表4 参数信息表

3 实测数据关联算法对比分析

为了验证算法的有效性，利用两批地波雷达的实测数据开展了分析，实验时间分别为2011年10月31日和2013年9月6日，实验区经纬度范围（35-40 N，117.5-123E）。实验数据包括覆盖实验区的地波雷达数据和同步AIS数据，如图5（a）～图5（b）。分别采用接近邻（nearest neighbor，N N）法与模糊方法对两批航迹做处理，航迹关联结果如图5（c）～图5（f），关联航迹首尾用细实线相连。从两者的整体关联效果和表5的统计来看，本文方法的关联率比N N法高。

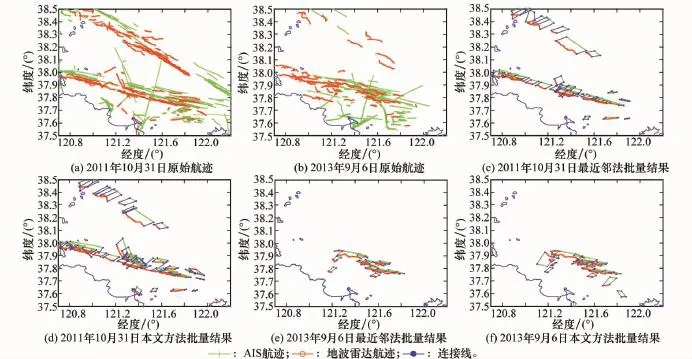
图5 2011年10月31日、2013年9月6日原始航迹及两种方法的关联结果

表5 关联结果统计

为了具体比对本文方法与最近邻法的航迹关联结果，在选取了2011年10月31日地波雷达与AIS航迹各两条作为个例，具体见图6（a）。其中HF1和HF2表示分别表示地波雷达航迹1和地波雷达航迹2，与其对应的实测AIS航迹分别是AIS1和AIS2。虽然从距离上看，AIS2与H F1距离较近，但从航迹的态势上看，AIS1与HF1、AIS2与HF2的态势相同，即AIS1与HF1关联，AIS2与HF2关联。使用最近邻法和模糊理论关联算法对上述四条航迹对进行了验证，两种方法的关联结果如图6（b）和6（c）所示。其中，采用模糊方法实现了正确关联，而采用NN法没有正确关联。

图6 2013.10.31航迹个例及关联结果

4 结束语

在对实测的地波雷达与AIS的航迹数据源做了分析的基础上，采用了基于模糊理论的航迹关联方法进行地波雷达与AIS之间的航迹关联研究，对关联方法中的展度、调整因子、权重等参数选取做了具体分析。使用两天的实测数据进行测试，结果表明本文方法航迹关联率高于最近邻法。另外，选取了地波雷达和AIS各两条航迹，分别采用最近邻法与本文的方法做了个例分析，发现在最近邻法无法实现正确航迹关联的复杂情况下，模糊方法能实现正确关联。

相比于最近邻法，模糊方法中采用了影响因子加权，增加了各关联影响因素的区分度，另外，模糊关联方法将关联的最终判定转换为关联质量因子的累积，增强了对干扰的抑制作用，提高复杂航迹的关联率。

［1］Ponsford A M，Sevgi L，Chan H C.A n integrated maritime surveillance system based on high-frequency surface-wave radars op-erational status and system performance［J］.Antennas and Propagation M agazine，2001，43（5）：52-63.

［2］Ponsford A M，D’Souza I A，Kirubarajan T.Surveillance of the 200 nautical mile E EZ using H FS W R in association with a spaced based AIS interceptor［C］∥Proc.of the IE E E Conference on Technologies for H omeland Security，2009：87-92.

［3］Vesecky J F，Laws K E，Paduan J D.Using H F surface wave radar and the ship auto matic identification system（AIS）to m onitor coastal vessels［C］∥Proc.of the IE E E International Conference on Geoscience and Remote Sensing Sy m posiu m，2009：761-764.

［4］Gurgel KW，Essen HH，Schl ick T.The university of hamburg W E R A H F radar-theory and solutions［C］∥Proc.of the International Radiowave Oceanography W orkshop，2001：19-25.

［5］Dzvonkovskaya A，G urgel KW，Rohling H，et al.Low power high frequency surface wave radar application for ship detection and tracking［C］∥Proc.of the International Conference on Radar，2008：：627-632.

［6］Dzvonkovskaya A，Gurgel KW，Rohling H，et al.H F radar W E R A application for ship detection and tracking［J］.European Journal of N avigation，2007，7（3）：18-25.

［7］Dzvonkovskaya A，Rohling H.H F radar performance analysis based on AIS ship information［C］∥Proc.of the Radar Conference，2010：1239-1244.

［8］Braca P，Grasso R，Vespe M，et al.A pplication of the JP D AU K F to H FS W radars for maritime situational awareness［C］∥Proc.of the15th International Conference on Inform ation Fusion，2012：2585-2592.

［9］Ji Y G，Zhang J，W ang Y M，et al.Ship detection point association and fusion with dual-frequency H F surface wave radar［J］. Systems Engineering and Electronics，2014，36（2）：266-271.（纪永刚，张杰，王鸣，等.双频率高频地波雷达船只目标点迹关联与融合处理［J］.系统工程与电子技术，2014，36（2）：266-271.）

［10］Ji Y G，Zhang J，M eng J M，et al.Point association analysis of vessel target detection with SAR，H FS W R and AIS［J］.Acta Oceanologica Sinica，2014，33（9）：73-81.

［11］Danul D，Sinha A，Kirubarajan T，et al.Fusion of over-the-horizon radar and automatic identification systems for overal l maritime picture［C］∥Proc.of the10th International Conference on Information Fusion，2007：1-8.

［12］W u S J，M ei X C.Radar signal processing and data processing technology［M］.Beij ing：Public House of Electronics Industry，2008：470-475.（吴顺君，梅晓春.雷达信号处理和数据处理技术［M］.北京：电子工业出版社，2008：470-475.）

［13］H e Y，Peng Y N.Fuzzy track correlation algorith ms for m ultitarget and multisensor tracking［J］.Acta Electronica Sinica，1998，26（3）：15-19.（何友，彭应宁.多目标多传感器模糊双门限航迹相关算法［J］.电子学报，1998，26（3）：15-19.）

［14］H e Y，W ang G H.Mutisensorinformation fusion with applications［M］.2nd ed Beijing：Public House of Electronics Industry，2010：116-172.（何友，王国红.多传感器信息融合及应用［M］. 2版.北京：电子工业出版社，2007：116-172.）

［15］Li Y L，Gao Z G，H an Y L.The determination of weight value and the choice of composite operators in fuzzy comprehensive evaluation［J］.Computer Engineering and Applications，2006，42（23）：38-42.（李玉琳，高志刚，韩延玲.模糊综合评价中权值确定和合成算子选择［J］.计算机工程与应用，2006，42（23）：38-42.）

纪永刚（1977-），通讯作者，男，副研究员，博士，主要研究方向为超视距雷达探测、海上目标多手段融合探测。

E-mail：jiyonggang@fio.org.cn

王 超（1990-），男，硕士研究生，主要研究方向为地波雷达信号处理。

E-mail：txouc2008@126.com

Track association for high-frequency surface wave radar and AIS based on fuzzy double threshold theory

LIU Gen-wang1，2，LIU Yong-xin1，JI Yong-gang2，3，W A N G Chao2
（1.College of Electronic Information Engineering，Inner M ongolia University，Hohhot010021，China；2.First Institute of Oceanography，State Oceanic A d ministration，Qingdao 266061，China；3.Oceanic Telemetry Engineering and Technology Research Center，State Oceanic A d ministration，Qingdao 266061，China）

A track association method based on fuzzy double threshold theory for high-frequency（H F）surface wave radar（HFSWR）and auto maticidentification system（AIS）is proposed.The membership degreeis adopted to describe the association degree between two tracks，and double threshold detection is used to determine the associated track pairs.Strategies on how to select the critical paramenters such as etaccouters，weights，and adjustment factors are analyzed；finally，two batches of measured data in October 31，2011 and September 6，2013 are em ployed to co m pare the nearest-neighbor association method and fuzzy association method，the result shows thatfuzzy methods has a higher association rate，and has better stability than nearestneighbor method in more complex situations.

high-frequency surface wave radar（H FS W R）；automaticidenti fication system（AIS）；track association

TN958

A

10.3969/j.issn.1001-506 X.2016.03.13

1001-506 X（2016）03-0557-06

2015-01-13；

2015-07-17；网络优先出版日期：2015-11-18。

网络优先出版地址：http：//www.cnki.net/kcms/detail/11.2422.TN.20151118.1208.010.html

国家海洋公益性行业科研专项（201505002）；国家自然科学基金（61362002）资助课题

刘根旺（1989-），男，硕士研究生，主要研究方向为雷达信号处理与数据融合。

E-mail：liu_genwang002@126.com

刘永信（1955-），男，教授，博士，主要研究方向为图像处理与模式识别、多传感器数据融合。

E-mail：yxliu@imu.edu.cn