基于P H D滤波的相控阵雷达多目标跟踪算法

袁常顺，王 俊，雷 鹏，孙进平，毕严先（北京航空航天大学电子与信息工程学院，北京100191）

基于P H D滤波的相控阵雷达多目标跟踪算法

袁常顺，王 俊，雷 鹏，孙进平，毕严先
（北京航空航天大学电子与信息工程学院，北京100191）

对于相控阵雷达方向余弦量测，采用扩展卡尔曼概率假设密度（extended Kalman probability hypothesis density，E K-P H D）滤波进行多目标跟踪时，存在目标数估计偏高和目标状态估计准确度低的问题。针对上述问题，提出了一种新的多目标跟踪算法——无偏转换量测概率假设密度（unbiased converted measurements P H D，U BC M-P H D）滤波算法。该算法采用方向余弦量测下的量测转换方法，保留了更多的量测信息；同时对转换后的量测偏差进行补偿，使量测转换误差的均值、方差准确近似原始量测高斯分布的一、二阶矩。仿真实验表明，所提算法可提高目标数和目标状态估计准确性。

相控阵雷达；多目标跟踪；无偏转换量测；随机有限集；概率假设密度滤波

网址：www.sys-ele.co m

0 引 言

在多目标跟踪中，目标数的变化和量测信息的不确定给多目标跟踪带来巨大的困难。如何有效、实时地实现多目标跟踪，一直是目标跟踪领域研究的热点和难点［1 3］。传统的多目标跟踪方法采用数据关联技术，但随着目标数或者杂波数的增加，其计算量指数增长，如：多假设跟踪（multiple hypothesis tracking，M H T）［2，4 5］、联合概率数据互联（joint probabilistic data association，JP D A）［1，6］、概率多假设跟_踪（probabilistic_ M H T，P M H T）［7］和多目标粒子滤波［8］。

近年来，Mahler以有限集统计学为基础，提出了随机有限集（random finite set，RFS）的方法。该方法提供了一个简洁的公式描述多目标跟踪，避免了数据关联，很快成为了多目标跟踪的研究热点之一［3，9 23］。通过随机有限集建模多目标状态和量测，多目标跟踪转换为对多目标后验密度估计的贝叶斯滤波。但由于多目标密度的组合特性和状态、量测空间的多维积分，导致多目标贝叶斯滤波在许多实际应用中无法实现［9 10］。为了解决这个困难，概率假设密度（probability hypothesis density，P H D）滤波作为多目标贝叶斯滤波的一阶矩近似被提出［9］。P H D滤波的优点是在单目标状态空间计算，避免数据关联。现有PHD滤波实现主要包括：高斯混合PHD滤波、扩展卡尔曼PHD（extended Kalman PHD，EKPHD）滤波、不敏卡尔曼PHD（unscented Kalman PHD，UKPHD）滤波［11］、粒子P H D滤波［10］，以及改进算法［12 14］。到目前为止，P H D滤波已经得到广泛应用，例如：即时定位与地图构建［15］、机动目标跟踪［16］、雷达目标跟踪［17］、图像序列跟踪［18］、扩展目标跟踪［19］、主动声学跟踪［20］、医学视频跟踪［21］等。

但是，对于P H D滤波在相控阵雷达应用的研究较少。相控阵雷达中，量测坐标通常为方向余弦坐标，因在方向余弦坐标下，天线方向图不随扫描角变化。采用E K-P H D滤波进行多目标跟踪时，由于E K-P H D滤波采用一阶泰勒级数近似，忽略高阶项，在滤波过程中引入了近似误差。针对这一问题，本文提出一种方向余弦坐标下无偏转换量测概率假设密度（unbiased converted measurements，U BC M-P H D）滤波的相控阵雷达多目标跟踪算法。该算法充分利用P H D滤波和无偏转换的优点，提高了滤波和目标数估计精度。算法首先根据非线性量测下的无偏转换方法，给出了方向余弦坐标下的无偏转换方法；然后将上述无偏转换方法与P H D滤波结合实现U BC M-P H D滤波。实验仿真验证了该算法对相控阵方向余弦坐标下多目标跟踪的准确性和有效性。本文的方法主要通过P H D滤波来实现，可直接被推广到势概率假设密度滤波［22］和势平衡多目标多伯努利滤波［23］。

1 RFS及P H D滤波原理

假设k时刻有M（k）个状态为xk，1，…，xk，M（k）的目标。传感器在k 时刻接收到N （k）个量测zk，1，…，zk，N（k）。在这些量测中，一部分是真实目标产生的量测，一部分是虚假量测，同时有些真实目标产生的量测无法被检测。基于RFS的多目标模型对目标状态和量测没有明确的顺序要求，所以其可被表示为有限集的形式，即

若k-1时刻目标状态为Xk-1，则k时刻的目标状态Xk可表示为

式中，Sk|k-1（ζ）为k-1时刻到下一时刻存活目标状态R FS；Bk|k-1（ζ）为k时刻由上一时刻状态ζ衍生目标状态R FS；Γk为k时刻新生目标状态R FS［9］。

k时刻接收量测Zk可表示为

式中，Κk为杂波量测RFS；Θk（x）为真实目标产生量测RFS［9］。

根据最优多目标贝叶斯滤波理论，基于R FS的多目标后验概率密度的递推表达式表示为

式中，fk|k-1（·|·）为状态转移概率密度函数；gk（·|·）为量测似然函数；μs为状态空间近似Lebesgue测度［9］。

由于式（3）和（4）多维积分的计算量庞大，实现复杂，文献［9］提出了利用多目标概率密度函数的一阶矩P H D近似多目标后验概率，实现对目标数时变且未知的多目标跟踪。令vk|k-1和vk分别为k时刻的预测P H D和后验P H D，则其可分别表示为

式中，βk|k-1（x）和γk（x）分别为衍生和新生目标状态R FS的预测P H D；pS，k（ζ）为k-1时刻状态ζ的目标在下一时刻存活概率；pD，k（x）为k时刻状态x的目标检测概率；κk（·）表示k时刻服从泊松分布杂波R FS的P H D［9］。

2 U BC M-P H D滤波

2.1 方向余弦坐标量测无偏转换

在多目标跟踪中，目标的状态通常采用笛卡尔直角坐标系描述，但传感器接收量测通常位于极坐标系或球坐标系。为了实现极坐标系或球坐标系的量测在笛卡尔直角坐标系下跟踪，量测转换方法被广泛的使用。近年来，出现了大量关于量测转换的改进算法［24 25］，其差异在于量测转换偏差和方差的估计方法。相控阵雷达由于阵列天线是不动的，当扫描波束偏离法线方向时，波速将会展宽，同时波束形状也有变化，若采用极坐标来分析会十分复杂，因此提出了方向余弦坐标。针对相控阵雷达方向余弦坐标系下的量测，本文给出了一种无偏量测转换方法，准确近似了原始量测高斯分布的一、二阶矩。

相控阵雷达量测为Zmcos=（Rmαm）T，假设真值为R，α，有

方向余弦量测噪声Vk=（）T为零均值高斯白噪声，其方差Rcos各分量为，。方向余弦坐标转换到直角坐标为

类似于式（7），得到直角坐标真值为

将式（8）带入式（9），化简后得到的转换误差为因此，直角坐标系下误差不再独立，且该误差与方向余弦、距离量测及原始量测误差有关。此外，的统计特性未知，且β与α有如下的非线性关系为了使方向余弦坐标系量测转换误差的均值、方差准确近似原始量测高斯分布的一、二阶矩，本文利用β在αm的四阶展开β4来近似，其误差为，则量测转换偏差和方差如下：

式（12）中

最终得到的无偏转换量测为Zcar=（αmRmβmRm）T+μ，方差为R。

2.2 U BC M-P H D

针对相控阵雷达的特点和E K-P H D滤波不足，本文提出了采用方向余弦坐标下无偏转换量测的方法和基于随机有限集的概率假设密度滤波对多目标进行跟踪，在保证跟踪精度的同时，实现对目标数精确的估计。该算法主要包含预测和更新两部分：预测部分与标准的高斯混合P H D滤波相同；更新部分采用无偏转换量测的方法将方向余弦坐标量测转换为直角坐标量测更新目标状态，具体如下。

预测 假设k-1时刻多目标后验概率密度的P H D为高斯混合形式，且可表示为

假设新生目标和衍生目标的P H D也分别为高斯混合形式，且表示为

根据前面的假设，k时刻预测的P H D也为高斯混合的形式，可表示为

式中

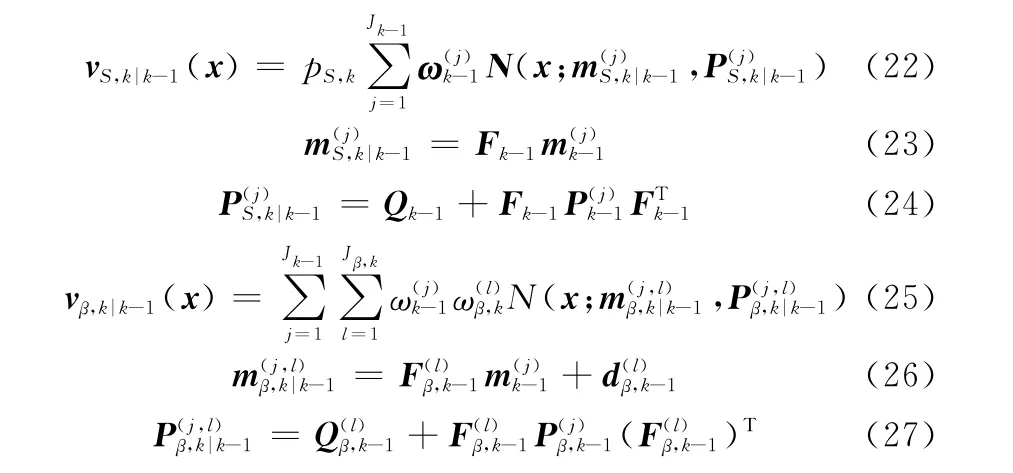
pS，k为目标存活概率。

更新 假设k-1时刻预测P H D为高斯混合形式

k时刻，对于每一观测z∈Zk，采用第2.1节给出的无偏转换量测的方式，求出该量测对应的转换偏差μk（z）和方差Rk（z）。则更新后的P H D可表示为

式中

该方法相比于文献［11］中的E K-P H D滤波，通过将量测误差转移到与目标状态相同的坐标中，在转换中由于各个变量之间不再是相互独立，因此转换后的方差可包含更多的信息。但由于在转换的过程中存在线性化误差的问题，采用去偏方式对转换后的量测进行补偿，同时给出了对应的转换方差，这样保证在转换过程中信息丢失最少，准确近似原始量测高斯分布的一、二阶矩，提高了算法跟踪性能。

3 仿真分析

采用一个目标数目时变且未知的二维相控阵雷达多目标跟踪场景来验证本文算法。目标的运动和量测模型分别表示为

仿真场景中共包含12个目标，起始时刻存在2个匀速运动的目标，接着分别有10个匀速和直角转弯运动的新生目标出现，真实运动参数如表1所示。新生目标R FS的P H D为

表1 目标真实运动参数

采样间隔取T=1 s，共采样100个时刻，对于E K-P H D和U BC M-P H D两种滤波算法的最多高斯分量数为100。仿真场景如图1所示，其中和□分别表示目标运动起始和结束位置。

图1 包含杂波量测的目标真实轨迹

图2给出了U BC M-P H D滤波算法单次仿真实验对多目标位置的估计结果。从仿真结果可以看出给出的算法可在大量虚警杂波中正确跟踪单独目标运动和不同的目标新生和消失量测。

图2 U B C M-P H D滤波位置估计

通过采用目标航迹固定但杂波量测随机产生的100次蒙特卡罗实验来验证算法的性能。图3和图4分别给出了E K-P H D和U BC M-P H D滤波算法的目标数估计均值和标准差比较结果。从图中可以看出，U BC M-P H D滤波算法的目标数估计均值更接近于真实目标数，E K-P H D滤波算法的目标数估计均值偏高；U BC M-P H D滤波算法的目标数估计标准差小于E K-P H D滤波算法。因为U BC M-P H D滤波算法在进行量测更新时，采用转换量测的方式将量测的误差全部转移到与运动状态相同的坐标系下，保留了更多的量测信息；同时本算法对转换后量测偏差进行补偿，使量测转换误差其均值、方差准确近似原始量测高斯分布的一、二阶矩，改善了滤波性能。但E K-P H D滤波算法采用一阶泰勒级数近似，忽略高阶项，在滤波过程中引入了近似误差，同时丢失部分量测信息。

图3 E K-P H D和U B C M-P H D目标数估计均值

图4 E K-P H D和U B C M-P H D目标数估计标准差

利用最优子模式分配（optimal subpattern assign ment O SP A）距离对以上算法性能进行综合评价，其定义为［26］

式中，p=1，c=300。

图5给出了两种算法的O SP A距离比较结果。从图中可知U BC M-P H D滤波算法的O SP A距离小于E K-P H D滤波算法，进一步表明本文提出的算法具有更高的跟踪精度；同时发现在目标数发生变化的时刻出现峰值，这主要是在目标新生的时刻，由于有新生目标加入，目标数出现变化，滤波器在该时刻对于目标数的估计偏离真实目标数（如图3所示）。

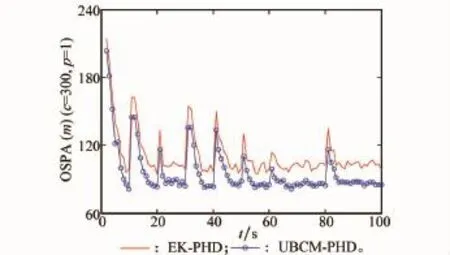
图5 E K-P H D和U BC M-P H D的O SP A距离

图6给出了在不同杂波密度ρc下两种滤波跟踪性能，其中检测概率pD，k=0.98。采用O SP A距离来进行比较，从比较结果可显著的发现U BC M-P H D滤波算法的性能优于E K-P H D滤波算法；同时随着杂波密度ρc的增加，两种算法的性能都降低。

图7给出了不同检测概率pD，k下两种滤波跟踪性能，其中杂波密度固定为ρc=31.25×10-3个/k m2。仍然采用O SP A距离来进行比较，从比较结果可以显著的发现两种滤波算法的跟踪性能随着pD，k的减小而变差。这主要是由于P H D滤波必须在解决比较高的检测不确定性的基础上接着解决目标数不确定，因此随着检测不确定的增加，目标的不确定性也增加了。但由于本文算法考虑了转换量测后偏差的补偿，因此跟踪性能会优于E K-P H D滤波算法。

图6 不同杂波率下的O SP A距离

图7 不同检测概率下的O SP A距离

4 结束语

在相控阵雷达中，量测坐标通常为方向余弦坐标，采用E K-P H D滤波算法进行多目标跟踪时，由于E K-P H D滤波采用一阶泰勒级数近似，忽略高阶项，在滤波过程中引入了转换误差。针对这一问题，本文提出了一种基于随机有限集的U BC M-P H D滤波算法，该算法采用转换量测的方式将量测误差转移到与运动状态相同的坐标系下，保留了更多的量测信息；同时对转换后的量测偏差进行补偿，使量测转换误差的均值、方差准确地近似原始量测高斯分布的一、二阶矩。仿真结果表明，本文所提算法可提高目标状态和目标数估计准确度。该算法主要通过P H D滤波来实现，可以直接被推广到势概率假设密度滤波和势平衡多目标多伯努利滤波。

［1］Bar-Shalom Y，Fortmann T E.Tracking and data association［M］. San Diego：Academic，1988.

［2］Black man S.Multipletargettracking with radar applications［M］. Norwood：Artech House，1986.

［3］M ahler R.Statistical multisource-m ultitarget inform ation fusion［M］.Norwood：Artech H ouse，2007.

［4］Reid D.A n algorith m for tracking m ultiple targets［J］.IE E E Trans.on Autom atic Control，2004，24（6）：843-854.

［5］Black man S.M ultiple hypothesis tracking for m ultiple target tracking［J］.IE E E Aerospace and Electronic Systems M agazine，2004，19（1）：5-18.

［6］Fortmann T E，Bar-Shalo m Y，Scheffe M.Sonar tracking of m ultiple targets using joint probabilistic data ssociation［J］. IE E E Journal of Oceanic Engineering，1983，8（3）：173-184.

［7］Streit R L，Luginbuhl T E.M axim u m likelihood method for probabilistic m ulti-hypothesis tracking［C］∥Proc.of the S PIE，1994：5-7.

［8］H ue C，Lecadre J P，Perez P.Sequential M onte Carlo methods for m ultiple target tracking and data fusion［J］.IE E E Trans.on Signal Process，2002，50（2）：309-325.

［9］M ahler R.M ultitarget Bayes filtering via first-order m ultitarget m o ments［J］.IE E E Trans.on Aerospace and Electronic Systems，2003，39（4）：1152-1178.

［10］V o B N，Singh S，Doucet A.Sequential M onte Carlo methods for m ultitarget filtering with rando m finite sets［J］.IE E E Trans.on Aerospace and Electronic Systems，2005，41（4）：1224-1245.

［11］Vo B N，M a W.T he Gaussian mixture probability hypothesis density filter［J］.IE E ETrans.on Signal Process，2006，54 （11）：4091-4104.

［12］Yang J L，Ji H B，Liu J M.Gauss-H ermite particle P H D filter for bearings-only m ulti-target tracking［J］.Systems Engineering and Electronics，2013，35（3）：457-462.（杨金龙，姬红兵，刘进忙.高斯厄米特粒子P H D被动测角多目标跟踪算法［J］.系统工程与电子技术，2013，35（3）：457-462.）.

［13］Chen L M，Chen Z，Yin F L，et al.Central difference Kalman probability hypothesis density filter for multi-target tracking［J］. Controland Decision，2013，28（1）：36-42.（陈里铭，陈喆，殷福亮，等.基于中心差分卡尔曼-概率假设密度滤波的多目标跟踪方法［J］.控制与决策，2013，28（1）：36-42.）

［14］Yan D L，Song Y D，Song Y，et al.T he application of squareroot cubature Kalman filter and probability hypothesis density in sim ultaneous localization and mapping for m obile robots［J］. Control Theory and A pplications，2014，31（8）：1009-1017.（闫德立，宋永端，宋宇，等.平方根容积卡尔曼滤波概率假设密度_省略_机器人同时定位与地图构建中的应用［J］.控制理论与应用，2014，31（8）：1009-1017.）

［15］A dams M，Vo B N，M ahler R，et al.SL A M gets a P H D：new concepts in map estimation［J］.IE E E Robotics&A utomation M agazine，2014，22（1）：26-37.

［16］Luo S H，Xu H，Xu Y，et al.U T based M M P H D filter for tracking maneuvering targets［J］.Systems Engineering and Electronics，2012，34（4）：666-672.（罗少华，徐晖，徐洋，等.基于U T变换的M M P H D机动目标跟踪［J］.统工程与电子技术，2012，34（4）：666-672.）

［17］Jan P，To mas S，Zdenek N，et al.A n optimization of a P H D function for association of targets on m ultistatic radar［C］∥Proc.of the IE E E Radar Conference，2014：1084-1089.

［18］V o B N，Vo B T，Pham N T，et al.Joint detection and estimation of m ultiple objects fro m image observations［J］.IE E E Trans.on Signal Procesing，2010，58（10）：5129-5241.

［19］Tian S P，Zhou B，Qi Q F.Gaussian mixture P H D filter based tracking m ultiple maneuvering extended targets［J］.Journalof Central South University（Science and Technology），2013，44 （12）：4923-4929.（田森平，周波，戚其丰.基于高斯混合P H D滤波的多机动扩展目标跟踪［J］.中南大学学报（自然科学版），2013，44（12）：4923-4929.

［20］Clark D，Vo B N，Bel l J.G M-P H D filter multitarget tracking in sonarimages［C］∥Proc.of the Defense and Security Symposium International Society for Optics and Photonics，2006：62350R-1 -62350R-8.

［21］Wood T M，Yates C A，Wilkinson D A，et al.Simplified multitarget tracking using the P H D filter for microscopic video data［J］. IE E E Trans.on Circuits and Systems for Video Technology，2012，22（5）：702-713.

［22］Vo B T，Vo B N，Cantoni A.A nalytic im plementations of the cardinalized probability hypothesis density filter［J］.IE E E Trans.on Signal Processing，2007，55（7）：3553-3567.

［23］Vo B T，V o B N，Cantoni A.The cardinality balanced m ultitarget m ulti-bernoulli filter and its im plementations［J］.IE E E Trans.on Signal Processing，2009，57（2）：409-423.

［24］Zhao Z，Li X R，Ji lkov V P.Best l inear unbiased fi ltering with nonl inear measurements for target tracking［J］.IE E E Trans.on Aerospace and Electronic Systems，2004，40（4）：1324-1336.

［25］M ei W，H e Z，Liang G.Iterated debiased Kalman filterfor target tracking with converted measurements［C］∥Proc.of the International Conference on Inform ation Science and Technology，2012：185-189.

［26］Schuh macher D，Vo B T，Vo B N.A consistent metric for performance evaluation of multi-object filters［J］.IE E E Trans.on Signal Processing，2008，56（8）：3447-3457.

Multi-target tracking based on P H D filter for phased array radar

Y U A N Chang-shun，W A N G Jun，L EI Peng，S U N Jin-ping，BI Yan-xian
（School of Electronics and Information Engineering，Beihang University，Beijing 100191，China）

The extended Kalman probability hypothesis density（E K-P H D）filter has a higher biasin the estimation of the number of targets and a lower estimation accuracy oftheir states by using the direction cosine coordinate measurements for the phased array radar.To solve this problem，a novel multi-target tracking algorith m called unbiased converted measurements probability hypothesis density（U BC M-P H D）filter algorith mis proposed.The proposed algorith mutilizes the unbiased converted method to remain more information about the direction cosine coordinate measurements.Meanw hile，it compensates the bias caused by the converting direction cosine coordinate to Cartesian coordinate measurements，and the means and variances of the converted errors could accurately approximate the first-order and second-order moments of Gaussian distribution for original measurements.The simulation results indicate that the proposed algorith mim proves the estimation accuracy of both the number of targets and their states.

phased array radar；multi-target tracking；unbiased converted measurements；random finite set；probability hypothesis density filter

T N 953

A

10.3969/j.issn.1001-506 X.2016.03.10

1001-506 X（2016）03-0539-06

2015-01-06；

2015-09-11；网络优先出版日期：2015-11-18。

网络优先出版地址：http：//www.cnki.net/kcms/detail/11.2422.T N.20151118.1208.012.html

国家自然科学基金（61171122，61201318，61471019，61501011，61501012）；中央高校基本科研业务费专项资金（Y W F-15-GJS Y S-068）资助课题

袁常顺（1987-），男，博士研究生，主要研究方向为雷达信号处理、随机有限集多目标跟踪。

E-mail：yuanchang61@126.com

王 俊（1972-），男，教授，博士，主要研究方向为雷达信号处理、实时信号处理。

E-mail：wangj203@buaa.edu.cn

雷 鹏（1985-），男，讲师，博士，主要研究方向为信号处理、频谱分析、目标识别。

E-mail：peng.lei@buaa.edu.cn

孙进平（1975-），男，教授，博士，主要研究方向为高分辨雷达信号处理、压缩感知等。

E-mail：sunjinping@buaa.edu.cn

毕严先（1988-），男，博士研究生，主要研究方向为雷达信号处理、目标识别。

E-mail：biyanxian@126.com