基于反演滑模控制的导弹制导控制一体化设计

齐 辉，张 泽，韩鹏鑫，许江涛，张德伟（.哈尔滨工程大学航天工程系，黑龙江　哈尔滨5000；.中国运载火箭技术研究院研究发展中心，北京00076）

基于反演滑模控制的导弹制导控制一体化设计

齐 辉1，张 泽1，韩鹏鑫2，许江涛1，张德伟1
（1.哈尔滨工程大学航天工程系，黑龙江哈尔滨150001；2.中国运载火箭技术研究院研究发展中心，北京100076）

针对传统制导和控制分开设计在拦截高速机动目标时的不足，给出了一种反演滑模一体化制导控制算法。首先利用微分几何理论，建立了一体化制导控制模型；然后根据平行接近原理，基于滑模控制和反演法，设计了一种反演滑模控制的导弹制导控制一体化算法；最后基于Lyapunov理论证明了系统的稳定性。数值仿真结果表明，所给出的一体化制导控制方法能够克服未建模的不确定性和目标机动干扰，具有较强的鲁棒性。

微分几何；制导控制一体化；反演法；滑模控制

网址：www.sys-ele.com

0 引 言

经典的导弹制导控制系统设计是将制导作为外回路和姿态控制作为内回路分开设计，这种设计忽略了制导回路和控制回路之间的耦合作用，系统间不能很好地匹配协调，对提高飞行器整体制导控制系统性能不利。特别是在制导末段因内外回路之间存在指令传输延迟，可能会导致系统的不稳定性和较大的脱靶量。

为了使制导回路和控制回路更好地协调工作，文献［1］将导弹的制导系统和控制系统作为整体进行设计。充分考虑导弹的姿控系统对其制导系统的作用，根据导弹和目标之间的相对运动方程和飞行器的姿态动力学方程直接设计控制指令，以此提高制导精度。近年来，制导控制一体化得到研究者的广泛关注，并取得了一定成果。基于最优控制理论，文献［2］利用θ-D方法解决了Riccati方程，从而设计出一种一体化控制律；文献［3］等利用滑模控制方法，将滑模面取为零效脱靶量，设计出了一种制导与控制一体化算法；文献［4］基于微分对策双边优化理论，采用终端投影法定义零效脱靶量和零效碰撞角作为状态变量，给出了一种一体化控制律；文献［5］基于动态面反演法，把导弹控制回路视为二阶环节，引入一阶积分滤波器来估计虚拟控制输入的导数，设计出了控制律。

本文针对俯仰平面内的拦截问题，基于微分几何理论建立了导弹制导控制一体化模型，在考虑模型非线性和目标干扰的不确定性条件下，结合反演法和滑模控制方法，给出了一种制导控制一体化算法，并对该算法的有效性进行了仿真验证。

1 导弹俯仰通道制导控制一体化建模

导弹与目标三维相对运动如图1所示。其中M为导弹质心，T为目标质心，r为二者之间相对距离，oxyz为参考惯性坐标系，ox4y4z4为视线坐标系，θL为弹目视线倾角，φL为弹目视线偏角。在视线坐标系中导弹与目标的加速度表示为和。

图1 导弹和目标运动关系

相对速度矢量在视线坐标系中表达式为

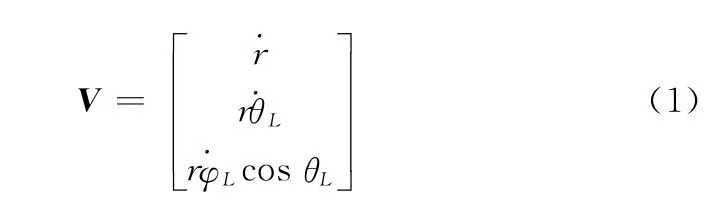
由绝对运动和相对运动的关系可得

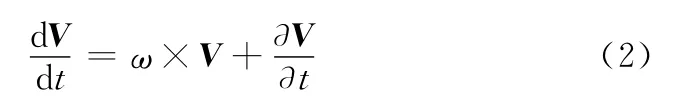
式中，ω为视线坐标系在参考惯性系中的旋转角速度：

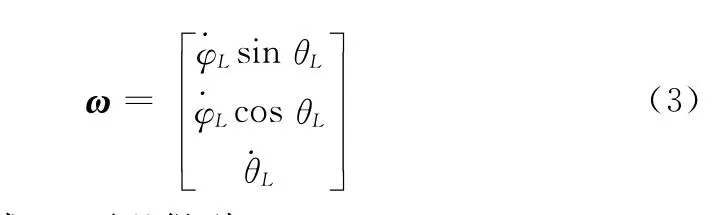
由式（1）～式（3）可以得到

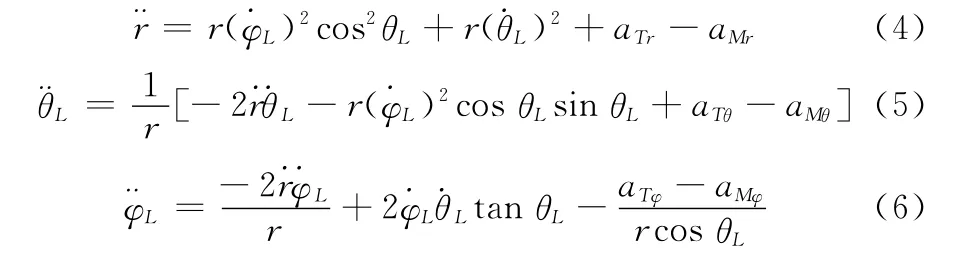
为了克服传统的导弹制导回路和控制回路分开设计存在指令传输延迟问题，将制导回路和控制回路作为一个整体进行设计。由于如果同时考虑目标机动和导弹气动建模带来的不确定性影响，其模型具有复杂的非线性特性，为了简化研究，考虑俯仰平面内的导弹制导控制一体化设计问题。一体化设计要同时考虑弹目相对运动和导弹的动力学方程。基于以上讨论，建立俯仰平面内的弹目相对运动方程为

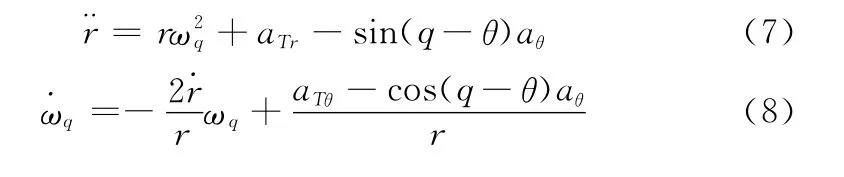
式中，ωq=，aθ=aMθ，q=θL，θ为导弹的速度方向角。

根据文献［3，7-8］，导弹俯仰通道内的动力学方程为

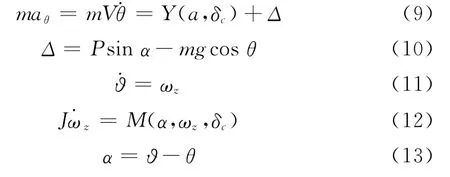
式中，Δ为导弹推力和重力对导弹加速度的作用，由于末制导段推力和重力对法向加速度的影响较小，因此这里将其视为不确定性；θ为导弹的速度方向角；Y为升力；α为导弹的攻角；δc为导弹俯仰舵偏角；为导弹的俯仰角；ωz为俯仰角速率；M为俯仰力矩；相比于俯仰力矩，俯仰舵对升力的作用较小，基于文献［3，7-8］可以得到

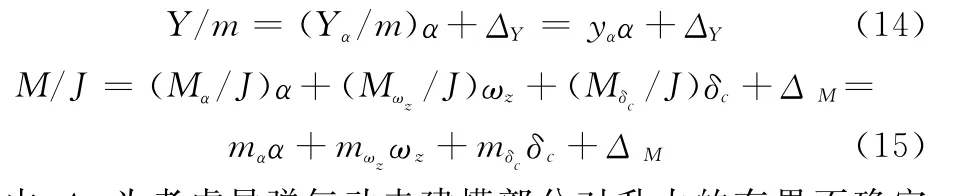
式中，ΔY为考虑导弹气动未建模部分对升力的有界不确定项；ΔM为考虑导弹气动未建模部分对俯仰力矩的有界不确定项。

在末制导阶段，导弹的轴向速度一般不可控，通过改变速度方向，基于平行接近原理，零化视线角速率，使导弹最终碰撞目标。综合弹目相对运动方程式（7）～式（8）和导弹动力学方程式（9）～式（15）可得制导控制一体化模型为

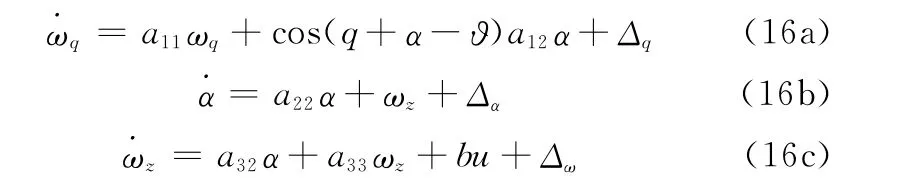
式中

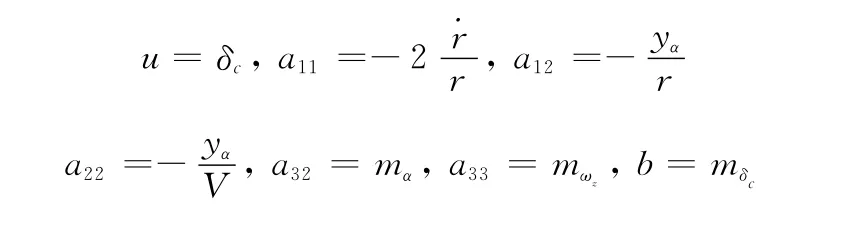
其中模型的不确定性项为

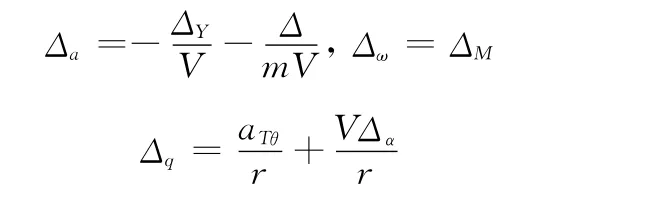
当r=0时是Δq的奇点，但是实际导弹和目标都有一定尺寸，二者相对距离减小至外壳相撞即可实现零脱靶量打击，因此在末制导阶段Δq有界。

一体化设计就是系统式（16）存在气动未建模不确定性Δα和Δw，以及目标扰动带来的不确定性Δq情况下，设计控制量u使弹目视线角速率趋于零，从而实现平行接近，对目标进行拦截。并保证系统稳定。

基于微分几何的状态反馈线性化理论［6］有如下结论。

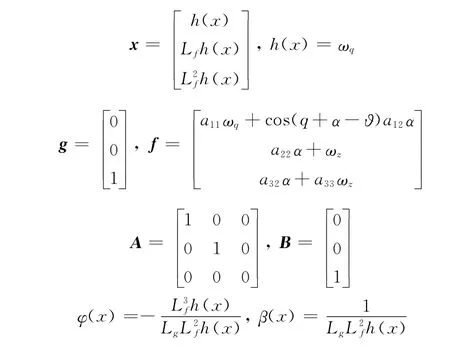
基于定理1，可得到如下可控线性系统：

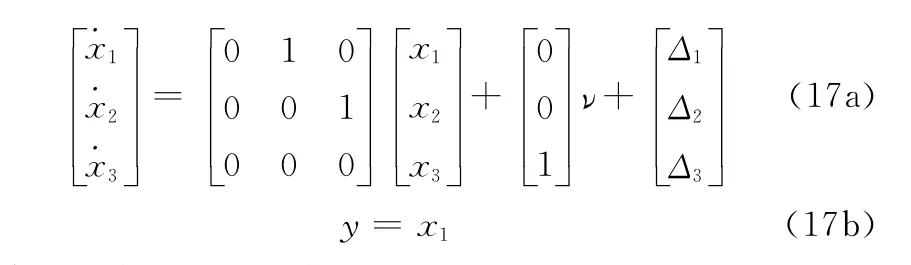
其中状态变量和系数如下：

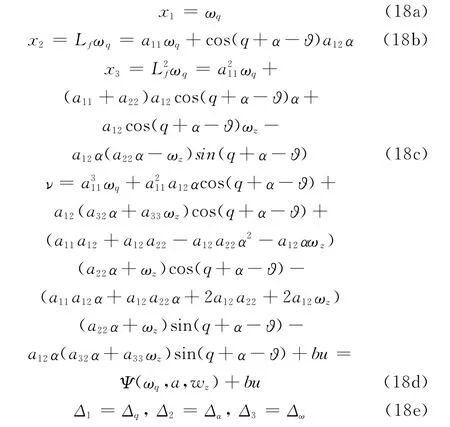
2 基于反演滑模控制的制导控制一体化设计

对控制系统式（17）的设计分为两部分，第一部分是反演算法，第二部分是滑模控制。

假设1 不确定性满足有界条件，即

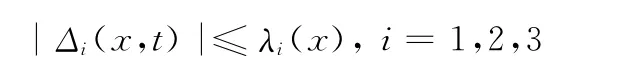
式中，λi（x）为已知的连续函数。

假设2 跟踪信息yd（t）连续有界，存在3阶导数，跟踪向量的范数是有界的，即对某正有界函数M＞0有‖Yd‖＜M。本文中期望信号yd（t）为ωq，希望收敛到零，所以假设2恒成立。

步骤1 反演算法

定义误差变量z1=x1-yd，则有

定义Lyapunov函数

对其求导得

设计虚拟控制

式中，c1，m和ρ为正常数。

定义误差变量

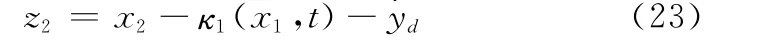
将式（23）代入式（19）得到

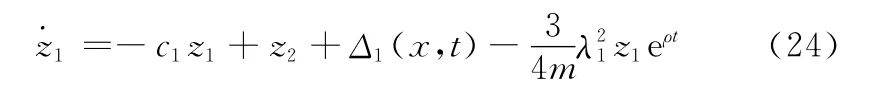
显然有

定义

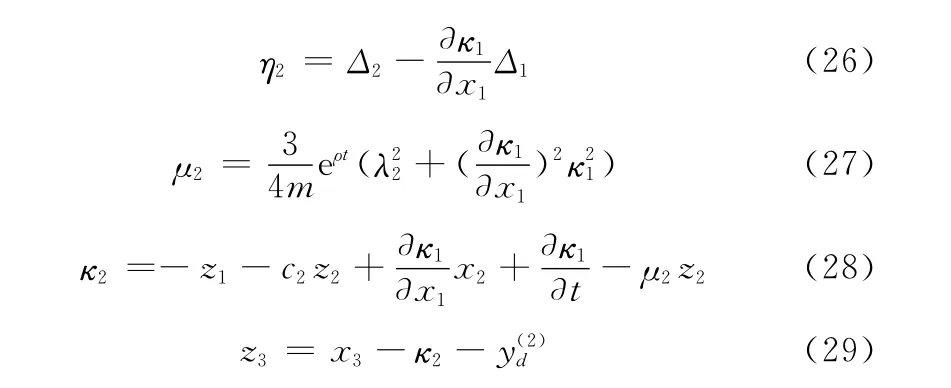
对式（23）求导可得

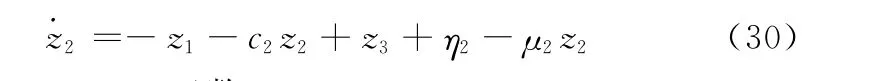
定义Lyapunov函数

对其求导得

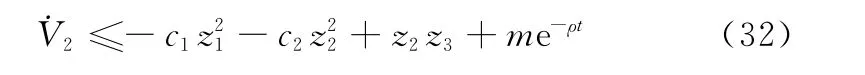
步骤2 滑模控制

考虑到滑模控制的强鲁棒性，设计如下的滑模面：

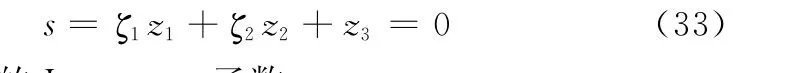
考虑如下的Lyapunov函数

对其求导可得

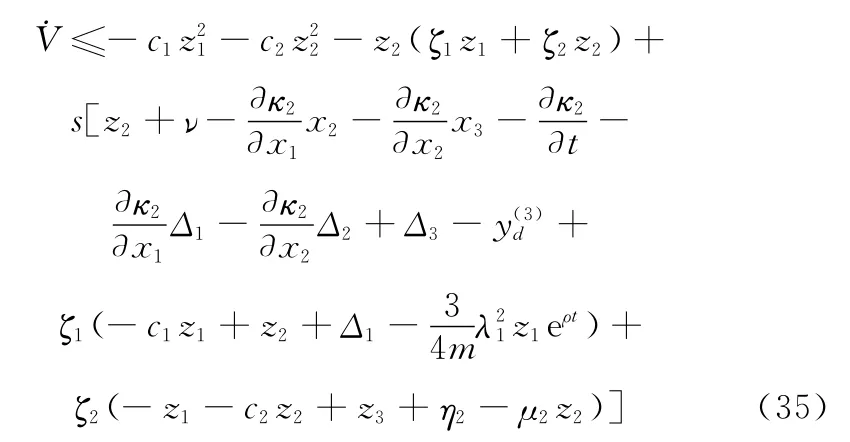
设计如下的滑模控制律：

式中，νeq为等效控制项，用来克服系统的非线性。

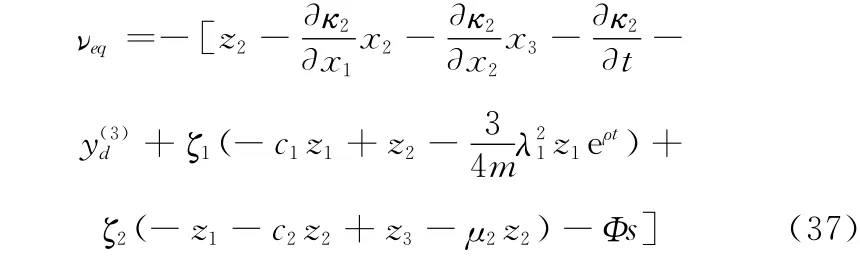
νsw为滑模切换项，克服系统的不确定性影响，设计

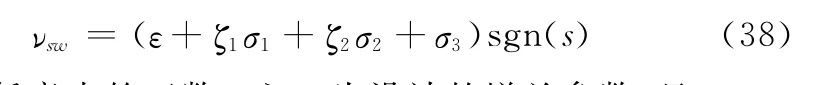
式中，ε为任意小的正数；Φ≥0为设计的增益参数，且

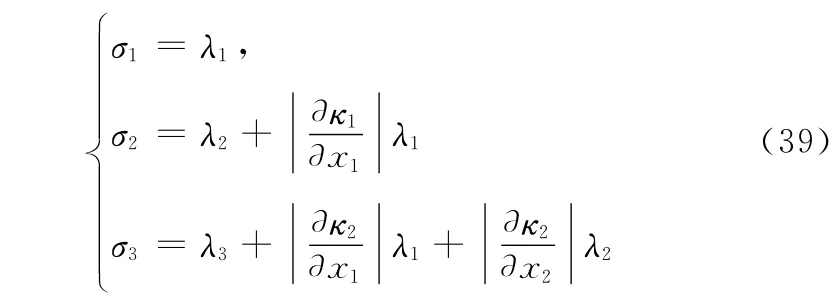
将式（36）～式（39）代入式（35）得到

所以由式（40）可知系统的稳定性得证。

为了获得期望的控制性能，适当调整增益Φ的值，增大Φ可以削弱抖振并减小滑模到达时间。根据式（18d）将控制律转换为实际系统的控制律为

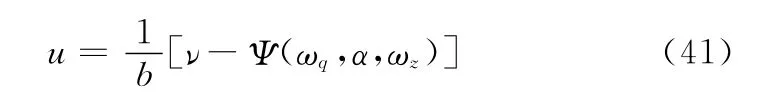
3 仿真及结果分析

为了验证所设计的导弹制导控制一体化算法的有效性，对其进行仿真分析。取导弹和目标的弹道倾角分别为-90°和-60°，速度分别取为V=380 m/s和VT=200 m/s。导弹及目标的初始条件如表1所示。

表1 仿真初始条件

导弹模型中的参数如表2所示。

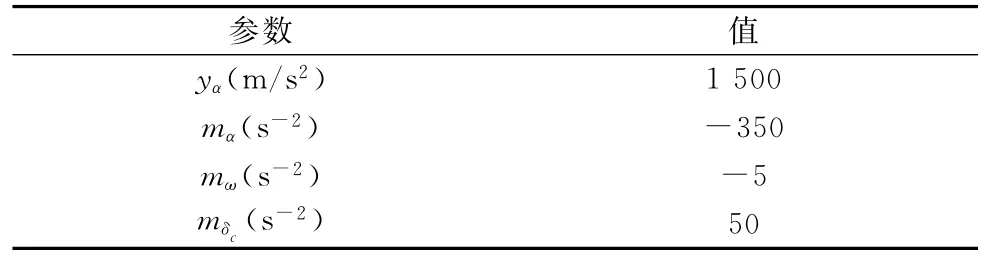
表2 导弹模型参数

气动建模和目标机动引起的有界不确定性项取为

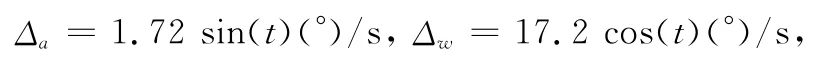
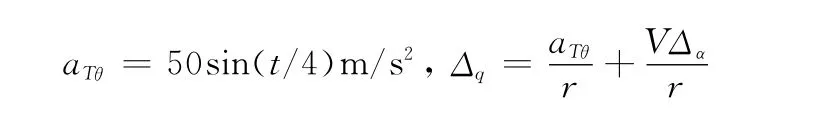
按照式（36）～式（41）所设计的控制律，取控制参数如下所示：

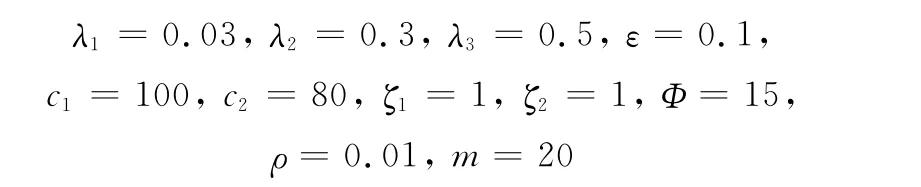
可以得到仿真结果如图2～图8所示。

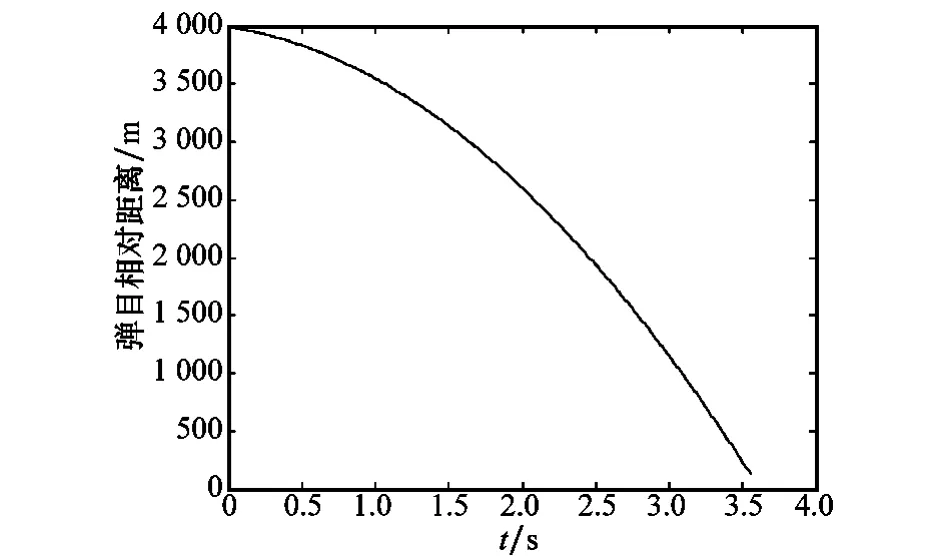
图2导弹和目标相对距离曲线

由图2可以看出经过3.5 s，导弹和目标的相对距离由最初的4 000 m小至0。这说明所设计的导弹制导控制一体化算法可以成功对目标进行拦截，实现精确打击的目的。

图3 视线倾角曲线

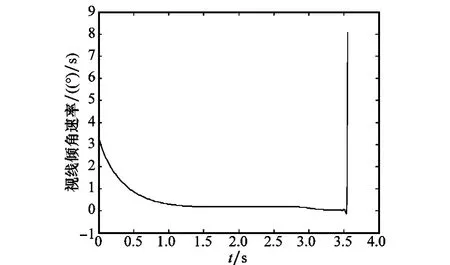
图4 视线角速率曲线

由图3可以看出，在整个末制导拦截过程中，弹目视线角由最初的-30°变为-28.4°，且变化过程平坦，变化幅度小。由图4可以看出，虽然系统建模中存在气动未建模不确定性Δα和Δw，以及目标扰动带来的不确定性Δq。但是按照所设计的一体化算法进行控制，在经历1 s后仍可以使视线角速率接近零，且保持在零附近。说明控制律可以保证系统状态成功进入滑模面实现平行接近，且系统能在滑模面中保持稳定，克服不确定性的影响，直到最终拦截到目标。

从图5和图6可以看出，导弹的俯仰角和俯仰角速率并未出现较大震荡。图7可以看出攻角经简短的快速调节后趋于零。说明进入滑模面后导弹的攻角和俯仰角均在合理的变化范围内，变化比较平滑，没有出现剧烈抖动，降低了对过载的要求，有利于实际物理条件的实现。

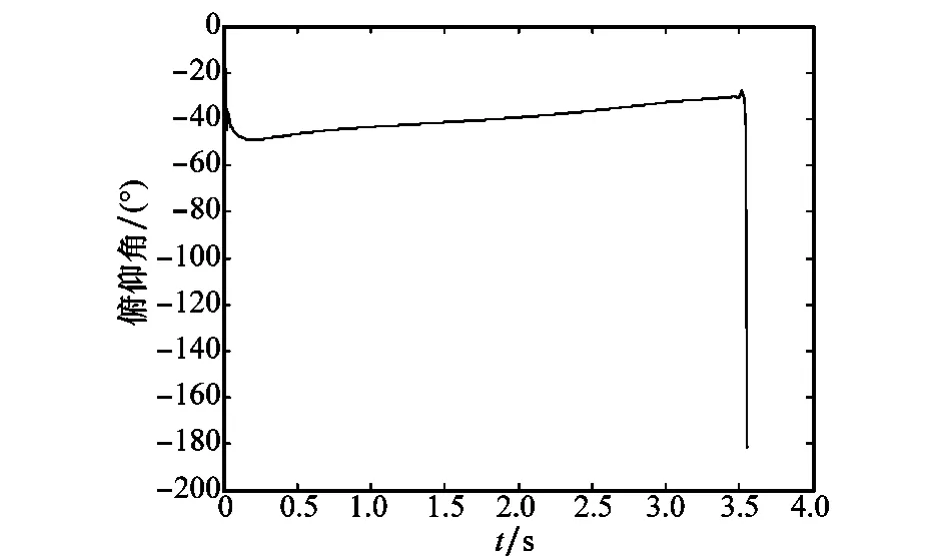
图5 俯仰角曲线

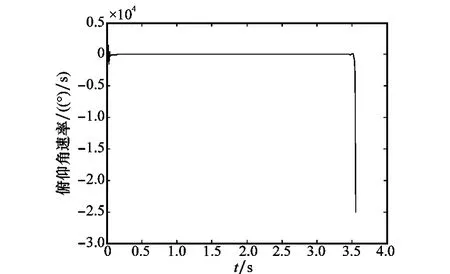
图6 俯仰角速率曲

图7 攻角曲线

在建立一体化模型时，为了消除模型中的非线性项，往往假设在末制导段q+α-是接近零的小量，所以有cos（q+ α-）≈1，由图8观察到前1秒这一假设并不成立。只有在滑模面内，此假设才近似成立。因此本文的结果更加符合实际，设计的制导控制一体化算法有较好的制导效果。

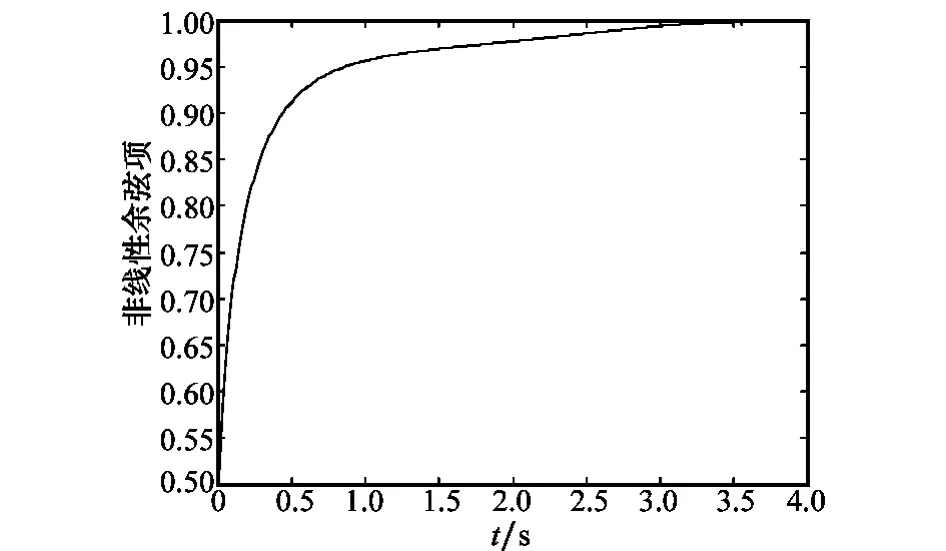
图8 cos（q+α-）曲线

4 结束语

本文对俯仰平面内制导控制一体化问题进行了研究。首先，基于微分几何理论建立了制导控制一体化数学模型。然后结合反演法和滑模控制法，设计了反演滑模控制器，并利用李雅普诺夫方法证明了系统的稳定性。结果表明：所提出的一体化设计方法在导弹存在气动未建模的不确定性和目标机动干扰情况下，仍能够保证弹目视线角速率趋于零并保持在滑模面内，且系统能够克服干扰保持稳定，从而实现平行接近目标对其进行拦截。

［1］Yueh L C F.O ptimal controller for ho ming missiles［C］∥Proc. of the IE E E A merican Control Conference，1984，137-142.

［2］Xin M，Balakrishnan S N，O hlmeyer E J.Integrated guidance and control of missiles withθ-d method［J］.IE E E Trans.on Control Systems Technology，2006，14（6）：981-992.

［3］Shima T，Idan M，Golan OM.Sliding m ode control for integrated missile autopilot guidance［J］.AIA A Journal of Guidance，Control，and D yna mics，2006，29（2）：250-260.

［4］H ua WH，Liu Y，Chen X L，et al.With a terminal constrained linear-quadratic differential game guidance law［J］.Acta Arm amentarii，2011，12（3）：1448-1455（花文华，刘杨，陈兴林，等.具有终端约束的线性二次型微分对策制导律［J］.兵工学报，2011，12（3）：1448-1455.）

［5］Zhou D.A guidance law with terminal impact angle constraint accounting for missile autopilot［J］.Journal of Dynamic Systems Measurement Control，2013，135（5）：1-10.

［6］Isidori A.Nonlinearcontrol systems［M］London：Springer-Verlag，1995：88-100.

［7］Sharma M，Richards N D.Adaptive integrated guidance and control for missile interceptors［R］.AIA A Paper，2004.

［8］Wise K A，Broy D J.Agile missile dynamics and control［J］.Journal of Guidance Control and Dynamics，1998，21（3）：441-449.

［9］Wang T H，Tahk M.Integrated back-stepping design of missile guidance and control with robust disturbance observer［C］∥Proc.of the SIC E-IC ASE International Joint Conference，2006：4911-4915.

［10］Dong F Y，Lei HM，Li J，et al.Design ofintegrated adaptive optimal sliding m ode guidance and control for interceptor［J］. Journal of Astronautics，2013，34（11）：1456-1461.（董飞垚，雷虎民，李炯，等.拦截弹自适应最优滑模制导和控制一体化设计［J］.宇航学报，2013，34（11）：1456-1461.）

［11］Shima T，Golan O.Linear quadratic differential game guidance law for dual control missiles［J］.IE E E Trans.on Aerospace Electronic System，2007，43（7）：834-842.

［12］Harl N，Balakrishnan S N.Impact time and angle guidance with sliding m ode control［J］.IE E E Trans.on Control Systems Technology，2012，20（6）：1436-1449.

许江涛（1975-），通讯作者，男，教授，博士研究生导师，主要研究方向为飞行器动力学、制导与控制。

E-mail：hit_xjt@163.com

张德伟（1978-），男，副教授，硕士，主要研究方向为弹性力学、飞行器动力学与控制。

E-mail：zhangdewei@hrbeu.edu.cn

Integrated design of missile guidance and control based on back-stepping and sliding mode control

QI H ui1，Z H A N G Ze1，H A N Peng-xin2，X U Jiang-tao1，Z H A N G De-wei1
（1.Department of Aerospace Engineering，Harbin Engineering University，Harbin 150001，China；
2.China Academ y of Launch Vehicle Technology R&D Center，Beijing 100076，China）

Aiming at the defects that the traditional design for guidance and controlis separated w hen intercepting high-speed maneuvering targets，an integrated algorithm for missile guidance and control based on backstepping and sliding is presented.Firstly，the integrated m ode of guidance and control is established based on the differential geometry theory.Then，according to the principle of parallel approach，an integrated algorithm of guidance and controlis proposed by using the method of back-stepping and the sliding mode control（S M C）technique.Finally，system stability has been proved based on the Lyapunov theory.The simulation results demonstrate that the design for the integrated method of guidance and control can overco me the interference of unmodeled dynamics uncertainty and target maneuver，which has strong robustness.

differential geometry theory；integrated guidance and control；back-stepping；sliding m ode control（S M C）

V 448

A

10.3969/j.issn.1001-506 X.2016.03.22

1001-506 X（2016）03-0618-06

2015-04-29；

2015-11-12；网络优先出版日期：2015-12-29。

网络优先出版地址：http：//w w w.cnki.net/kcms/detail/11.2422.T N.20151229.1744.008.html

国家自然科学基金（11372080）；哈尔滨市科技局青年创新人才基金（2014R F Q XJ121）资助课题

齐 辉（1963-），男，教授，博士研究生导师，主要研究方向为飞行器动力学、弹性力学。

E-mail：qihui205@sina.com

张 泽（1990-），男，硕士研究生，主要研究方向为飞行器动力学、制导与控制。

E-mail：280979024@qq.com

韩鹏鑫（1983-），男，博士，主要研究方向为飞行器制导与控制。

E-mail：hanpengxin_hit@163.com