基于自适应渐消F K F的FastSL A M算法

刘 丹，段建民，于宏啸（北京工业大学城市交通学院，北京100124）

基于自适应渐消F K F的FastSL A M算法

刘 丹，段建民，于宏啸
（北京工业大学城市交通学院，北京100124）

快速同时定位与建图（fast sim ultaneous localization and mapping，FastSL A M）算法的采样过程会带来粒子退化问题，为了改进算法的性能，提高估计精度，从研究粒子滤波的建议分布函数出发，提出基于自适应渐消扩展卡尔曼滤波（adaptive fading extended Kalman filter，A FE K F）的FastSL A M算法。该算法基于FastSL A M的基本框架，利用A FE K F产生一种参数可自适应调节的建议分布函数，使其更接近移动机器人的后验位姿概率分布，减缓粒子集的退化。因此在同等粒子数的情况下，该算法有效提高了SL A M精度，以此减少所使用的粒子数，降低算法的复杂度。基于模拟器和标准数据集的实验仿真结果验证了该算法的有效性。

快速同时定位与建图；粒子退化；自适应渐消扩展卡尔曼滤波；建议分布函数

网址：w w w.sys-ele.co m

0 引 言

同时定位与建图（simultaneous local ization and mapping，SL A M）是指移动机器人在未知环境中探索时，根据自身携带的传感器建造环境地图，并在建造的地图中确定自身的位置。SL A M问题被称为自主移动机器人界的“圣杯”［1 2］。

SLAM问题针对的是未知且不确定的环境，目前常用的两种解决方法［3］：一种是基于扩展卡尔曼滤波的SL A M （extended Kalman filter-SL A M，E K F-SL A M）算法；另一种是快速同时定位与地图构建（fast simultaneous localization and mapping，FastSL A M）算法。然而随着SL A M问题研究的深入，发现E K F方法在实际应用中存在很多问题，包括算法复杂度高，线性化误差大以及数据关联复杂等问题［4-5］，这些都严重限制其在SL A M研究领域的应用范围。M ontemerlo于2003年提出了基于Rao-Blackwellized particle filter的FastSL A M算法［6］。FastSL A M算法有两个版本：FastSL A M 1.0和FastSL A M 2.0［7］。FastSL A M 1.0算法通过粒子滤波器来估计移动机器人的位姿，用E K F来完成环境特征位置的估计［8］。虽然FastSL A M 1.0算法在一定程度上很好地解决了E K F-SL A M计算复杂度过高等问题，但其将SL A M问题的过程模型直接作为建议分布，没有融合最新的测量信息，这使得算法存在较大缺陷，容易导致算法运行过程中粒子严重退化［9］，进而导致SL A M发散。为了解决这个问题，FastSL A M 2.0采用E K F算法对移动机器人位姿进行递归估计，得到估计均值和方差，因而产生的建议分布函数中融入了移动机器人的环境观测信息，使得粒子集中分布于移动机器人真实位姿附近［7］。因此，FastSL A M 2.0算法的性能比FastSL A M 1.0算法整体上有所提高。针对FastSL A M算法中如何获取更接近粒子后验概率分布的建议分布函数问题，文献［10］在FastSL A M 2.0算法基础上提出了基于无迹卡尔曼滤波的FastSL A M算法，用无迹卡尔曼滤波（unscented Kalman filter，U K F）来估计粒子的后验位姿建议分布，提高粒子采样精度，进而提高系统状态估计的精度。文献［11-12］提出了基于迭代扩展Kalman滤波（iterated extended Kalman fi lter，IE K F）建议分布的FastSL A M算法，运用IE K F使得粒子分布于高观测似然区域。因此，在FastSL A M2.0的基础上，探讨如何获得一个可自适应调节的建议分布函数，来降低粒子退化程度，提高SL A M的精度，是本文工作的研究重点。

引入文献［13-16］中所用的渐消滤波，将其与E K F融合，产生一种参数可自适应调节的建议分布函数，使系统具有更好的自适应性和鲁棒性［16］；并且该函数使粒子可以更好地近似状态变量的后验概率密度函数，降低粒子的退化程度［3］，从而有效提高对移动机器人位姿的估计精度。因此本文提出了基于自适应渐消E K F的FastSL A M算法，可简称为：自适应渐消FastSL A M（adaptive fading sim ultaneous localization and mapping，A FFastSL A M），即在该算法递归估计过程中，由A FE K F来产生粒子重要性采样函数，用粒子滤波估计移动机器人的位姿，E K F来完成地图的预测和更新。

1 传统的FastSL A M算法

1.1 SL A M问题的描述

从概率角度来说，在线SL A M问题是一个关于如何根据移动机器人前一时刻的位姿、观测信息以及控制输入信息来求得下一时刻位姿和环境地图的联合后验概率问题［8］，联合后验概率表示为

式中，xt表示t时刻移动机器人的位姿；u1∶t和z1∶t分别表示控制信息和观测信息c1∶t=［c1，c2，…，ct］表示从1时刻到t时刻的数据关联；m表示环境地图，每一个环境特征表示为mj。利用贝叶斯公式，将后验概率表示为

式中，ct=｛η1，η2，…，ηM｝表示t时刻各个路标元素之间的数据关联；ηj=k表示观测信息中第j个观测点与地图中第k个路标为同一路标；ηj=表示观测测信息中第j个观测点与地图中路标关联失败；η表示归一化常数。

1.2 FastSL A M算法的基本思想

FastSL A M算法的基本思想是把SL A M系统的状态估计分解为对移动机器人运动路径的递归估计和基于估计路径的环境特征位置估计［8 9］，表示为

式中，N表示地图特征的个数。在FastSL A M算法中采用粒子滤波器进行路径估计，每一个粒子都保存一份地图，再将地图估计分解为N个独立的环境特征估计，每个环境特征采用一个扩展卡尔曼滤波器进行估计，因此在FastSL A M算法中，若粒子数为M个，则总共有M×N个扩展卡尔曼滤波器。t时刻第i个粒子的数据结构表达式为［8］

2 基于自适应渐消F K F的FastSL A M算法

FastSL A M算法是利用粒子滤波器进行位姿估计，而粒子滤波的退化问题却是无法避免的，退化问题的根源在于粒子滤波方法中使用的粒子点并不是从后验分布中抽样出来的，而是从建议分布函数中抽样得到的［17］；由于建议分布和后验分布之间的差异，随着算法的迭代，必然出现退化问题，所以建议分布函数选取的好坏，对权重方差的大小、退化问题的严重程度影响很大［17］，进而直接影响SL A M的估计精度。针对这个问题提出了基于自适应渐消E K F的FastSL A M算法，该算法对单个粒子的建议分布采用自适应渐消E K F获得。

2.1 自适应渐消F K F

以非线性离散随机系统模型为例［13］，即

式中，xt、zt分别表示t时刻系统的状态向量和观测向量；f为关于状态的非线性函数；随机系统噪声wt-1～N（0，Q）；随机观测噪声vt～N（0，R）。则基本的E K F方程为

（1）状态预测

（2）卡尔曼增益

（3）状态更新

传统的E K F成为A FE K F的充分条件是在线选择t时刻的时变滤波增益矩阵Kt使得式（12）和式（13）成立［18］。

式中，γt是新息，式（12）是E K F状态估计新息最小方差性能指标；式（13）表示在不同时刻的输出新息序列要互不相关，建立在式（12）和式（13）基础上的A FE K F通过引入渐消因子λt，使得式（14）成立。

即输出的新息序列是互不相关的，从物理意义上理解，表示这一滤波器与通常的E K F相比可更大限度地将有效信息从新息中提取出来，因此，A FE K F能高精度地跟踪状态量，在应对过程参数变化的鲁棒性方面也有所改善［13］。令

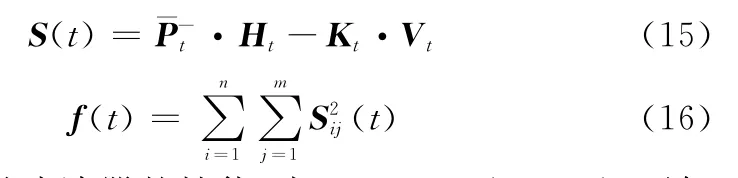
式（16）用来衡量滤波器的性能，由于S（t）=｛Sij（t）｝，可知当f（t）取值越小，滤波性能就越好，则应选择λt使f（t）最小。由式（15）可知最优时应满足

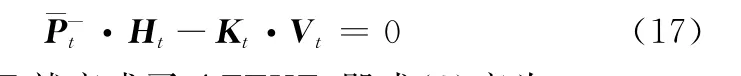
此时的E K F就变成了A FE K F，即式（8）变为

式中，λt为自适应渐消因子，限定其最小值为1。即

λt的求解过程就是将式（9）和式（18）代入式（17）中，可得到

其中

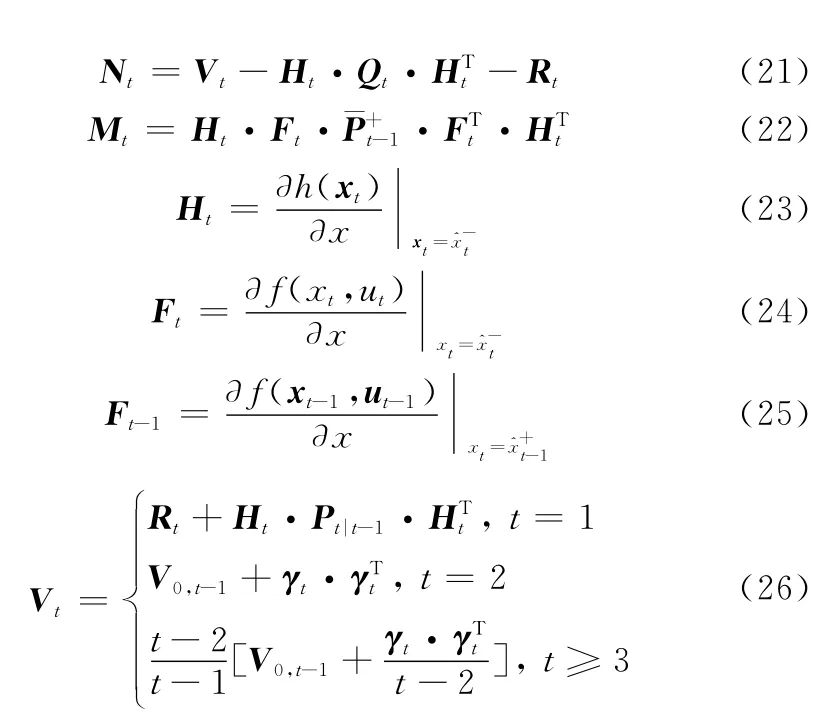
则式（20）化简为：Nt=Mt·λ，两边求迹，近似得到：

上述过程与一般的E K F相比，预测协方差矩阵前面多乘了一个自适应渐消因子λt，其物理意义是：过程参数发生变化或在不精确的噪声统计情况下，新息的增大会引起Vt的增大，进而使得Nt增大，由λt的算式可以看出，λt相应增大，滤波器的估计能力增强，使系统状态估计迅速收敛到真实值附近，此时滤波性能达到最佳。这就意味着采用渐消E K F时，能够减小陈旧观测值对估计的影响，使系统具有更好的自适应性和鲁棒性，进而提高了滤波器的估计精度［19］。

2.2 AFFastSL A M算法

2.2.1 位姿估计（建议分布计算）

改进的算法中，利用A FE K F产生粒子的建议分布函数，采用粒子滤波器来进行位姿估计。位姿估计过程包含位姿预测和位姿更新两个阶段。

（1）位姿预测

首先预测t时刻移动机器人位姿的均值和方差，即

式中，ut表示控制输入信息；f表示运动模型方程；表示t-1时刻移动机器人的位姿表示t时刻的位姿预测均值。

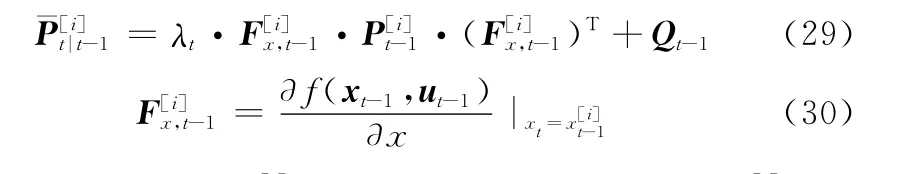
式中，λt为渐消因子为位姿预测协方差矩阵表示函数f对位姿x求得的雅克比矩阵表示上一时刻位姿估计方差；Qt-1表示控制噪声的协方差矩阵。

（2）位姿更新

当观测的路标信息与已经建立的地图中的路标信息匹配时，即索引为j的环境路标被移动机器人重新观测到，则执行更新步骤

此时根据渐消自适应E K F思想，利用式（20）～式（27）计算得到λt，进而通过式（35）～式（37）计算更新后位姿的均值和方差

t时刻，若移动机器人同时观测到多个环境路标，且其都存在于已经建立的地图中，则需要依次根据每一个路标的观测值对移动机器人的位姿均值x及其协方差进行更新，每次更新均以前次更新结果作为初始值。更新完毕后，得到建议分布函数N由于渐消因子λt对权值方差进行调节，可以更准确地提取有效信息，抑制突变状况对控制模型和观测模型的影响，使得到的建议分布函数更接近真实的分布［16，19］。

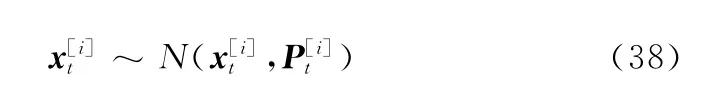
对每个粒子计算权值：

并归一化权值

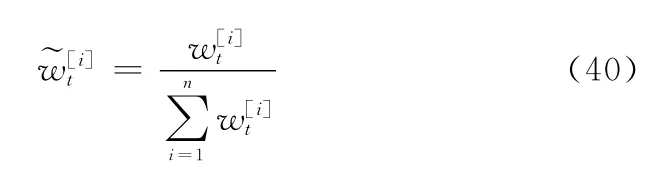
2.2.2 环境地图估计

传统FastSL A M算法中，将地图估计分解为N个特征估计问题，并通过E K F来估计地图中路标的条件概率分布。由于地图中的每个环境特征均服从独立的二维高斯分布，所以雅可比矩阵是一个2×2的矩阵，计算量相对较小［3，20］，计算效率比较高，此时，E K F相比U K F［10］，IE K F［11 12］以及粒子滤波等算法都有明显的计算优势，因而基于自适应渐消扩展Kalman滤波的FastSL A M算法中的每一个粒子，在更新完移动机器人位姿的部分后，利用E K F算法对环境路标进行更新。在此阶段需要对当前时刻的重复观测路标和首次观测路标采用不同的策略进行处理。

（1）当t时刻观测的索引为j的路标信息与已建立地图中的某些路标经过数据关联能够匹配时，更新的过程如下：

首先，在移动机器人位姿已知的前提下，对索引为j的路标的预测观测值计算公式为

式中，Kj，t表示路标更新卡尔曼增益；表示t-1时刻的路标j的估计方差。

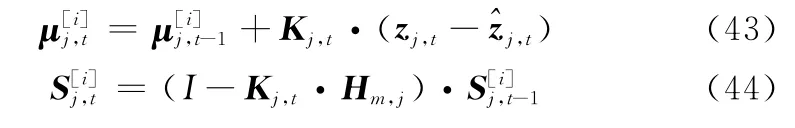
式中，zj，t表示t时刻第j个环境路标的真实测量值；和分别表示更新后第j个路标的均值和方差。

（2）t时刻，第一次观测到索引为n的环境路标时，需计算路标的全局坐标并将其加入所建的地图中，具体过程为

式中，zn，t为观测值；分别表示首次观测到路标的均值和方差。

2.2.3 重采样

除了通过获取最优的建议分布函数，来解决粒子退化问题外，重采样方法在一定程度上也会缓解粒子的退化现象。重采样的基本思想是抛弃那些重要性权重很小的粒子点，而复制权重较大的粒子点来替代它们。但重采样也会带来一些问题，它使得小权重粒子大量消失，大权重粒子被反复复制，致使粒子多样性变差而发生粒子贫化现象，造成滤波精度下降。文献［21］提出了以一种改进的重采样算法，按照局部重采样算法对粒子进行分类，中等权重的粒子保持不变，大权重和小权重的粒子采用Tho m pson-Taylor算法进行随机线性组合产生新粒子。文献［11］将复制的粒子与伪抛弃组中的粒子进行线性组合，提出了线性优化重采样方法，这些改进算法在一定程度上都降低了粒子的贫化程度，保证了粒子的多样性，但算法的运算复杂度增加。本文提出算法中应用的重采样方法是由文献［22］提出的自适应重采样。首先设定一个阈值3N/4，N为粒子数，然后计算粒子集的有效粒子数Neff。若Neff小于设定的阈值，则对粒子集进行系统重采样。Neff可以由式（48）近似计算得到。

此重采样方法相对简单，运算效率高，但是在确保粒子多样性问题上还存在不足，因此在未来的工作中会研究如何获得一个衡量粒子退化程度的度量函数，来解决何时进行重采样，多少粒子需要重采样等问题，来减少重采样计算量，保证粒子多样性，提高滤波精度，进而提高SL A M精度。

2.2.4 算法流程

综上，改进的t时刻的SL A M算法具体过程如下：

设粒子数N，控制噪声Q，观测噪声R。

步骤1 初始化粒子集S0=；从先验分布中随机抽取采样点，令其权值为其中N为粒子数。

步骤2 重要性采样：首先利用A FE K F计算粒子的后验位姿建议分布，然后从建议分布中进行采样得到新一代粒子（式（38）），并计算其重要性权重（式（39））。

步骤3 对于已经存储在粒子中的重复性观测路标，根据式（41）～式（44）更新其状态以及协方差矩阵。

步骤4 对于第一次被观测到的路标，根据式（45）～式（47）初始化环境路标的状态均值和协方差矩阵，并加入所建立的环境地图中。

步骤5 按照式（48）计算粒子集的Neff，如果Neff≤3N/4，则对粒子集进行系统重采样。

3 仿真结果

为了验证提出算法的性能，分别基于模拟器和“Car Park Dataset”数据集的实验仿真对A FFastSL A M、U FastSL A M、FastSL A M 2.0进行比较，程序的运行环境为M atlab2012b，使用的计算机CP U型号为Intel（R）Core （T M）i5-3470，主频为3.2 G Hz。

3.1 基于模拟器的实验仿真

利用文献［23］开发的SL A M算法模拟器，对提出的A FFastSL A M算法与U FastSL A M，FastSL A M 2.0算法的性能进行对比。

仿真环境如图1所示，在这个环境中包含了移动机器人行走的路径和环境路标（星号“*”），其中，这些路标都是静态路标。在仿真中用到的运动学模型和环境模型如式（49）和式（50）所示，其中运动学模型为后轮驱动模型。仿真实验中，机器人的移动速度为3 m/s，最大转向角为30°，轴距为2 m，激光雷达最大的观测范围为20 m，观测频率为50 Hz，控制时间间隔为0.025 s。

图1 基于模拟器的仿真环境

输入：xv（t-1）为移动机器人在t-1时刻的位姿，dt为传感器采样时间，v为速度，G为机器人在t时刻的方向角，W B为轴距。输出：xv（t）为机器人的新位姿。

输入：（xj，yj）为激光雷达探测到的第j个特征的位置坐标，xv（t）为移动机器人的位姿。输出：路标特征点与移动机器人的距离r以及与机器人前进方向的夹角θ。

3.1.1 算法性能的比较

（1）不同测量噪声条件下的算法性能比较

仿真中设定粒子数为10个，控制噪声设为（0.3 m/s，3°）；观测噪声分别设置5组：（0.04 m，0.6°）、（0.07 m，0.8°）、（0.1 m，1°）、（0.2 m，3°）、（0.4 m，4°），对于每组观测噪声，均对A FFastSL A M算法、U FastSL A M算法、FastSL A M 2.0算法进行50次蒙特卡罗仿真实验［7，24］，并将50次仿真的移动机器人位姿的均方根误差（root meansquare error，R M SE）均值（评估SL A M估计精度）及标准差（评估SL A M执行稳定性）作为评价标准［7，24］，R M SE的计算公式如式（51）所示，实验结果如图2所示，其中线棒代表R M SE标准差，柱状代表R M SE均值。可见随着噪声增加，3种SL A M算法对移动机器人位姿估计的R M SE均值和标准差都逐渐增加，但是A FFastSL A M算法对移动机器人位姿估计的R M SE均值要低于U FastSL A M和FastSL A M 2.0两种算法，而且较之另外两种算法，A FFastSL A M算法对应的RS M E标准差增长速度也相对缓慢，因此提出的算法具有较高的估计精度、较强的抑制噪声能力和自适应能力。

式中，N为每次SL A M仿真中离散采样点的数量；sk为移动机器人的实际位姿；为移动机器人的估计位姿。

图2 不同测量噪声条件下的3种算法R M SE

（2）粒子数目不同条件下的算法性能比较

研究提出的算法在增长粒子数条件下的性能［7，24 25］。其中粒子数分别设定为5，10，30，50，70，100，控制噪声设为（0.2 m/s，1°），观测噪声为（0.1 m，0.8°），分别对3种SL A M算法进行30次仿真，实验结果如图3所示，可以看出，随着粒子数的增多，3种算法的位姿估计的R M SE均值都逐渐降低，即位姿估计精度越来越高，但是要达到相同的位姿估计精度，提出的SL A M算法所需要的粒子数要少于其他两种算法使用的粒子数，所以提出的算法可以使用更少的粒子达到更高的精度，而且能够保证计算效率。

图3 不同粒子数下的3种算法R M SE

3.1.2 算法复杂度的对比

提出算法和U FastSL A M、FastSL A M 2.0算法的复杂度都主要取决于路径估计、地图估计、权重计算、以及粒子重采样这4个步骤的计算复杂度［25 26］。假设粒子数M个，环境特征点N个，传感器一次观测到n个特征，其中，k个特征已经存在于地图中，则计算建议分布的复杂度为O（M*k）；粒子权重的计算复杂度与粒子的数目成正比，即为O（M），更新地图的复杂度为O（M*n）；对于重采样阶段，首先需要计算有效粒子数Neff，其复杂度为O（M），同时每个粒子中都存有各自的特征地图，因此重采样的复杂度为O（M*N）。以表1为例，提出的算法和其他两种算法的复杂度基本相同，但是要达到同样的估计精度，提出的算法要比其他两种算法中所用的粒子数少，即O（M）＜O（M1）＜O（M2）。如表2所示，当位姿估计的R M SE均值大致相同时，A FFastSL A M所需要的粒子数要少于U FastSL A M和FastSL A M 2.0；而且如表3所示，在采用相同粒子数进行算法仿真实验时，提出算法所得到的位姿估计精度是最高的，其运行时间也远小于U FastSL A M，但由于提出算法中存在计算自适应渐消因子的环节，所以其执行时间相比FastSL A M 2.0有所增加。因此要获得更准确的SL A M结果，应用提出的算法会降低计算的复杂程度，提高SL A M过程的计算效率，同时因重采样导致的粒子贫化程度也会相对降低。

表1 3种算法复杂度对比表

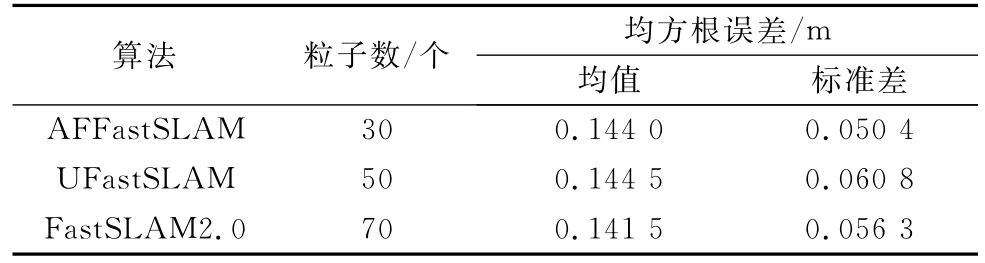
表2 均方根误差近似相等时的粒子数比较

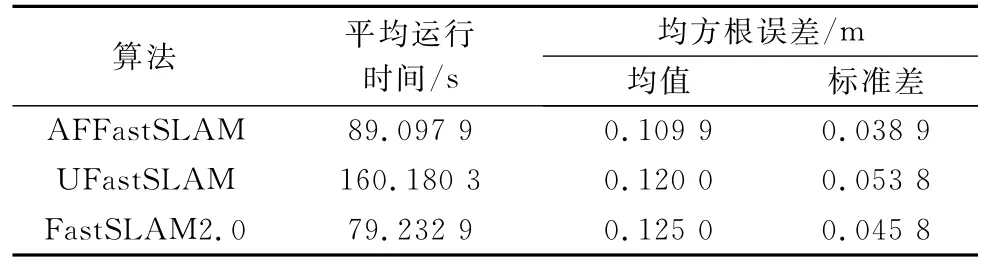
表3 粒子数为100时均方根误差和运行时间对比表

3.2 基于标准数据集的实验仿真

采用悉尼大学地面移动机器人中心（A CF R）提供的“Car Park Dataset”数据集对SL A M算法进行仿真研究，该数据集是SL A M研究领域的一个标准数据集，其数据包和相关文档均可以在文献［27］中获得。该数据集的实验地点位于一个卫星数量较多，能够获取高质量GPS信息的30× 45 m2的校园停车场内，实验平台为一个配备有里程计、前轮偏角传感器，激光雷达、全球定位系统（global position systerm，G PS）的四轮汽车，在实验中使用60 m m的钢管作为人造路标；激光雷达作为环境感知传感器；G PS用于获取车辆和路标的定位信息，其数据仅用来评价SL A M算法的性能，并不参与SL A M过程的运算［7］。如图4所示，仅仅根据里程计和前轮偏角传感器测得的车辆速度和转向角，通过航迹推算得到的车辆路径，会偏离G PS测得的实际路径［7，25］。

图4 “Car Park Dataset”数据集的G PS路径和航迹推算路径

利用“Car Park Dataset”数据集，对A FFastSL A M、U FastSL A M、FastSL A M 2.0算法进行对比研究。仿真实验中，控制噪声设为（0.7 m/s，7°）；观测噪声设为（0.1 m，1°）；粒子数设为50个。图5表示提出的算法和其他两种算法的仿真结果，可以看出，A FFastSL A M使得估计路径与G PS产生的真实路径吻合程度更高，相对应的路标估计也更准确，因此A FFastSL A M性能要优于U FastSL A M和FastSL A M 2.0。

图5 “Car Park Dataset”数据集的SL A M实验结果

为了进一步进行量化分析，得到了图6所示的位姿估计误差曲线和图7所示的路标估计误差曲线。图6（a）和图6（b）分别表示车辆在x轴和y轴方向的位姿估计误差，不难看出，所提算法的位姿估计误差要小于其他两种算法，其中提出算法位姿估计的误差最大为0.919 1m，而U FastSL A M和FastSL A M 2.0算法的最大位姿误差分别为1.155 0 m和1.208 2 m。如图7所示，提出算法的路标估计误差要小于FastSL A M 2.0算法，而在第5和第6个路标点处的估计误差，提出算法要大于U FastSL A M算法中产生的误差，但提出算法对整个地图估计的精度要大于U FastSL A M算法。由图6和图7量化分析得出，所提算法相比其他两种算法具有更好的定位精度和地图构建精度。

图6 位姿估计误差曲线

图7 路标估计误差曲线

为了更准确的评估提出算法的性能，基于该数据集，在粒子数均选取30个的前提下，对3种SL A M算法分别进行10次蒙特卡罗仿真实验，并以10次实验的位姿估计和路标估计的R M SE的均值和标准差作为评价标准，结果如图8所示，图中曲线表示R M SE均值，线棒表示R M SE标准差。可以看出，提出的算法得到的位姿估计和路标估计的R M SE均值均低于U FastSL A M算法和FastSL A M2.0算法，这意味着提出的算法对移动机器人位姿的估计精度和地图构建精度都要优于其他两种算法，而且从位姿估计和路标估计的RS M E标准差变化趋势中可以看出，提出算法的运行稳定性较强。

图8 位姿估计和路标估计的均方根误差

4 结 论

本文将渐消滤波的思想引入到FastSL A M2.0算法中，提出了一种基于自适应渐消E K F的FastSL A M算法，该算法在产生建议分布函数时，融入了最新环境观测值，利用渐消因子自适应的调节权值，充分提取有效信息，使之得到的建议分布函数更加贴近后验分布函数，从而提高了SL A M预测过程的粒子采样效率，保证了粒子的收敛性。实验结果表明，与U FastSL A M，FastSL A M2.0算法相比，提出的算法降低了粒子的退化程度，提高了SL A M精度，能够在粒子数较少的情况下较精确地完成移动机器人的同时定位与建图。

［1］Durrant-W hyte H，Bailey T.Sim ultaneous localization and mapping：part I［J］.IE E E Trans.on Robotics and Autom ation M agazine，2006，13（2）：99-110.

［2］Bailey T，Durrant-W hyte H.Sim ultaneous localization and mapping：part II［J］.IE E E Trans.on Robotics andA utomation M agazine，2006，13（3）：108-117.

［3］Zhou W，Zhao C X.A FastSL A M 2.0 algorithm based on genetic algorithm［J］.Robot，2009，31（1）：25-32.（周武，赵春霞.一种基于遗传算法的FastSL A M 2.0算法［J］.机器人，2009，31（1）：25-32.）

［4］H olmes S，Klein G，M urray D W.A n O（N2）square root unscented Kalman filter for visual sim ultaneous localization and mapping［J］.IE E E Trans.on Pattern Analysis and M achine Intelligence，2009，31（7）：1251-1263.

［5］H wang S Y，Song J B.M onocular vision-based SL A M in indoor environ ment using corner，lam p，and door features fro m upward-looking ca mera［J］.IE E E Trans.on Industrial Electro-nics，2011，58（10）：4804-4812.

［6］M ontemerlo M.FastSL A M：a factored solution to the sim ultaneous localization and mapping problem with unknow n data association［D］.Pennsylvania：Carnegie M ellon U niversity，2003.

［7］Song Y，Li Q L，Kang Y F，et al.SL A M with square-root cubature Rao-Black willised particle filter［J］.Acta A utom atica Sinica，2014，40（2）：357-367.（宋宇，李庆玲，康轶非，等.平方根容积Rao-Black willised粒子滤波SL A M算法［J］.自动化学报，2014，40（2）：357-367.）

［8］T hrun S，M ontemerlo M，K oller D，et al.FastSL A M：an efficient solution to the sim ultaneous localization and mapping problemwith unknow n data association［J］.M achine Learning，2004，4（3）：380-407.

［9］Tang W J，Zhang G L，Jing B.Co m parative study of FastSL A M algorith m for m obile robot［J］.Com puter Engineering and Design，2012，33（3）：1165-1169，1180.（汤文俊，张国良，敬斌.移动机器人FastSL A M算法的对比研究［J］.计算机工程与设计，2012，33（3）：1165-1169，1180.）

［10］Kim C，Sakthivel R，Chung W K.U nscented FastSL A M：a robust and efficient solution to the SL A Mproblem［J］.IE E E Trans.on Robotics，2008，24（4）：808-820.

［11］W ang H J，W ang J，Liu Z Y.Fast sim ultaneous localization and mapping based on iterative extended Kalman filter proposal distribution and linear optimization resa m pling［J］.Journal of Electronics&Inform ation Technology，2014，36（2）：318-324.（王宏健，王晶，刘振业.基于迭代扩展Kalman滤波建议分布和线性优化重采样的快速同步定位与构图［J］.电子与信息学报，2014，36（2）：318-324.）

［12］Zhan L，Zhao C X.A new FastSL A M algorith m based on iterated E K F［J］.Journal of Shandong University （Engineering Science），2012，42（4）：41-47.（张丽，赵春霞.一种基于迭代E K F的FastSL A M算法［J］.山东大学学报（工学版），2012，42 （4）：41-47.）

［13］Zhou DH，Xi Y G，Zhang Z J.Suboptimal fading extended Kalman filtering for nonlinear systems［J］.Control and Decision，1990，3（5）：1-6.（周东华，席裕庚，张钟俊.非线性系统带次优渐消因子的扩展卡尔曼滤波［J］.控制与决策，1990，3 （5）：1-6.）

［14］Yang L Q，Xiao Q G，Niu Y，et al.Design oflocalization system based on reducing Kalman filter［J］.Journal of N anjing University of Aeronautics&Astronautics，2012，44（1）：134-138.（杨柳庆，肖前贵，牛妍，等.基于渐消卡尔曼滤波器的定位系统设计［J］.南京航空航天大学学报，2012，44（1）：134-138.）

［15］Xu D J，H e R，Shen F，et al.A daptive fading Kalman filter based on innovation covariance［J］.Systems Engineering and Electronics，2011，33（12）：2696-2699.（徐定杰，贺瑞，沈锋，等.基于新息协方差的自适应渐消卡尔曼滤波器［J］.系统工程与电子技术，2011，33（12）：2696-2699.）

［16］Gong Y S，Gui QM，Li B L，et al.A daptive fading extended Kalman particle filtering applied to integrated navigation［J］. Geodesy and Geodyna mics，2010，30（1）：99-103.（宫轶松，归庆明，李保利，等.自适应渐消扩展Kalman粒子滤波方法在组合导航中的应用［J］.大地测量与地球动力学，2010，30 （1）：99-103.）

［17］Du Z C.Particle fi lter and the research of its appl ication in MIMO wireless com munication［D］.Chengdu：University of Electronic Science and Technology，2008.（杜正聪.粒子滤波及其在MIMO无线通信中的应用研究［D］.成都：电子科技大学，2008.）

［18］W ang H J，Fu G X，Li J，et al.Strong tracking C K F based SL A Mmethod for un manned underwater vehicle［J］.Chinese Journal of Scientific Instru ment，2013，34（1）：2543-2550.（王宏健，傅桂霞，李娟，等.基于强跟踪C K F的无人水下航行器SL A M［J］.仪器仪表学报，2013，34（1）：2543-2550.）

［19］Gao S S，Xue L，W ei WH.Fading adaptive U PF algorith m and its application to integrated navigation［J］.Journal of N orthwestern Polytechnical University，2012，30（1）：27-31.（高社生，薛丽，魏文辉.渐消自适应Unscented粒子滤波及其在组合导航中的应用［J］.西北工业大学学报，2012，30（1）：27-31.）

［20］W ang H，Ding J D，Fang B F，et al.Particle filter algorith m based on genetic optimization method［J］.Frontiers of Computer Science and Technology，2012，6（10）：927-934.（王浩，丁家栋，方宝富，等.融合遗传优化的粒子滤波器算法［J］.计算机科学与探索，2012，6（10）：927-934.）

［21］Chang T Q，LI Y，Liu Z R，et al.Particle filter algorith m based on im proved resa m pling［J］.A pplication Research of Com puters，2013，30（3）：748-750.（常天庆，李勇，刘忠仁，等.一种改进重采样的粒子滤波算法［J］.计算机应用研究，2013，30（3）：748-750.）

［22］Doucet A，Godsill S，A ndrieu C.O n sequential M onte Carlo sam plingmethods for Bayesian filtering［J］.Statistics and Com puting，2000，10（3）：197-208.

［23］Bai ley T，Nieto J，Nebot E.Consistency of the FastSL A M algorithm［C］∥Proc.of the Robotics and Automation，2006：424-429.

［24］Song Y，Li QL，Kang YF，et al.Effective cubature FastSL A M：SL A M with Rao-Black wellized particle filter and cubature rule for Gaussian weighted integral［J］.A dvanced Robotics，2013，27（17）：1301-1312.

［25］H avangi R，Taghirad H D，Nekoui M A，et al.A square root unscented FastSL A M with im proved proposal distribution and resam pling［J］.IE E E Trans.on Industrial Electronics，2014，61（5）：2334-2345.

［26］Zhu J H，Zhen NN，Yuan Z J，et al.A SL A M algorith m based on central difference particle filter［J］.Acta A utom atica Sinica，2010，36（2）：249-257.（祝继华，郑南宁，袁泽剑，等.基于中心差分粒子滤波的SL A M算法［J］.自动化学报，2010，36 （2）：249-257.）

［27］Nieto J，G uivant J，Nebot E，et al.Real time data association for FastSL A M［C］∥Proc.of the Robotics and A utomation，2003：412-418.

FastSL A Malgorith m based on adaptive fading extended Kalman filter

LIU Dan，D U A N Jian-min，Y U H ong-xiao
（College of M etropolitan Transportation，Beijing University of Technology，Beijing 100124，China）

Sampling process often causes particle degradation in fast simultaneous localization and mapping （FastSL A M）.Fro m the point view of the proposal distribution function，a method named the FastSL A M based on adaptive fading extended Kalman filter is proposed to improve the performance of the algorith m and increase estimation accuracy.It uses the adaptive fading extended Kalman filter（A F E K F）to co m pute proposal distribution based on the basic framework of FastSL A M，then this proposal distribution is m ore close to the posterior position of the m obile robot and the degree of particle degradation is reduced.In the case of the same number of particles，the algorith m can effectively improve the accuracy of SL A M.Henceit can reduce the number of particles used in the algorith m and the complexity of the algorithm.The validity of the proposed algorith m is verified by the experimental simulation results based on the simulator and the standard data set.

fast sim ultaneous localization and mapping（FastSL A M）；particle degradation；adaptive fading extended Kalman filter（A F E K F）；proposal distribution

T P 242.6

A

10.3969/j.issn.1001-506 X.2016.03.26

1001-506 X（2016）03-0644-08

2014-12-15；

2015-07-21；网络优先出版日期：2015-09-17。

网络优先出版地址：http：∥w w w.cnki.net/kcms/detail/11.2422.T N.20150917.1659.004.html

北京市教委基金项目（JJ002790200802）资助课题

刘 丹（1990-），女，博士研究生，主要研究方向为智能车辆的同时定位与建图。

E-mail：danaliu@yeah.net

段建民（1959-），男，教授，博士研究生导师，主要研究方向为车辆环境识别与自动驾驶技术、网络化测控系统与现场总线技术、嵌入式汽车电子控制技术。

E-mail：jm duan@bjut.edu.cn

于宏啸（1986-），男，博士研究生，主要研究方向为智能车辆横纵向控制。

E-mail：yhxiao321@gmail.com