基于ADAMS的不完全齿轮机构设计与运动分析
田野王惠源 杨志远 刘雪松 牛碧凯、山西中北大学 、中国兵器工业第二〇八研究所
基于ADAMS的不完全齿轮机构设计与运动分析
田野1王惠源1杨志远1刘雪松2牛碧凯2
1、山西中北大学2、中国兵器工业第二〇八研究所
本文利用计算得到的不完全齿轮齿面数据,在CAXA中建立不完全齿轮机构的齿廓曲线,然后将曲线导入UG中建立机构的三维模型,并利用ADAMS软件建立虚拟样机,最后将理论计算与仿真结果进行对比分析。仿真结果中,机构的运动停歇次数和动停比与理论值基本一致,机构的运动满足设计要求。从动轮在每次运动的开始时刻冲击较大,表明不完全齿轮机构一般只适用于低速、轻载的场合。
不完全齿轮;虚拟样机;运动学分析
引言
在机械运动方案设计中,常常需要实现瞬时停歇运动和带有停歇区间的断续性运动,由于不完全齿轮机构主、从动轮的假想齿数和主、从动轮上锁止弧的数目以及锁止弧之间的实际齿数均可在相当大的范围内自由选择,因而有关间歇运动的一些特性参数可以调整的幅度要比槽轮机构大得多,设计比较灵活。
本文在已有结论的基础上,建立不完全齿轮机构的虚拟样机,对该机构运动进行仿真分析,并将仿真结果与理论值对比,为该机构的理论分析与设计运用提供依据。
1 不完全齿轮机构设计要求
该不完全齿轮机构的设计要求为从动轮每一次转角ψ2=90°,即在自身回转一周过程中运动与停歇各四次,N=2π/ψ2=4。主动轮回转一周过程中,从动轮运动与停歇各一次,其运动时间与停歇时间比(动停比k)为0.25~0.35。
选择初始条件,取主动轮上假想齿数z1=48,从动轮上假想齿数z2=48,模数m=2,分度圆压力角α=20°,从动轮齿顶高系数h*a2=1。
2 不完全齿轮机构参数计算
2.1主动轮首、末齿齿顶高系数的确定
不完全齿轮机构在停歇期间,通常从动轮的轮齿与连心线处于对称位置。设计不完全齿轮机构时以此对称位置为准。若不完全齿轮机构有关参数选择不当,则有可能发生在此对称位置主动轮1的齿顶被从动轮2的齿顶顶住而不能进入啮合的情况,称为不完全齿轮的齿顶干涉现象。为了避免齿顶干涉现象,需要设计主动轮首、末齿齿顶高系数。

图1 主动轮首、末齿齿顶高系数的确定
从动轮顶圆压力角:

从动轮顶圆齿厚所对中心角之半:

一对标准齿轮齿顶圆的两个交点间所对从动轮中心角之半:

单齿传动(z1’=1)中,从动轮每次运动所转角度中的齿数K=[K’]=
单齿传动(z1’=1)中,从动轮每次转角δ2=2πK/z2=0.3927rad=22.5°
开始啮合时,与从动轮首齿相啮合的从动轮齿厚中心线与连心线间夹角γ2= (K-1)π/z2=0.13089rad=7.5°
因此系数G=-z2(z1+z2)-2(z1+1)+(z1+z2)(z2+2)cos(δ2-θ2-γ2)=-51.0228
主动轮首齿齿顶高系数按h*a1’≤h*a1'',取h*a1’=0.4。
2.2锁止弧设计
为保证不完全齿轮机构的正常运转,要求从动轮每次运动终止时停留在预定的对称位置,所以机构上应该安装定位装置。通常在主、从动轮上切制锁止弧来满足这个要求。
2.2.1从动轮锁止弧的设计

图2 从动轮锁止弧的设计
如图2所示为从动轮锁止弧,为考虑有一定的强度,齿顶不产生尖角,锁止弧不通过个齿两侧的齿顶尖角,留有0.5m的齿厚。
从动轮顶圆齿厚为0.5m时所对中心角λ2=1/(z2+2h*a2)=0.02rad=1.15°
从动轮锁止弧半径可由ΔO1O2E’中求得:

2.2.2主动轮锁止弧起点的确定
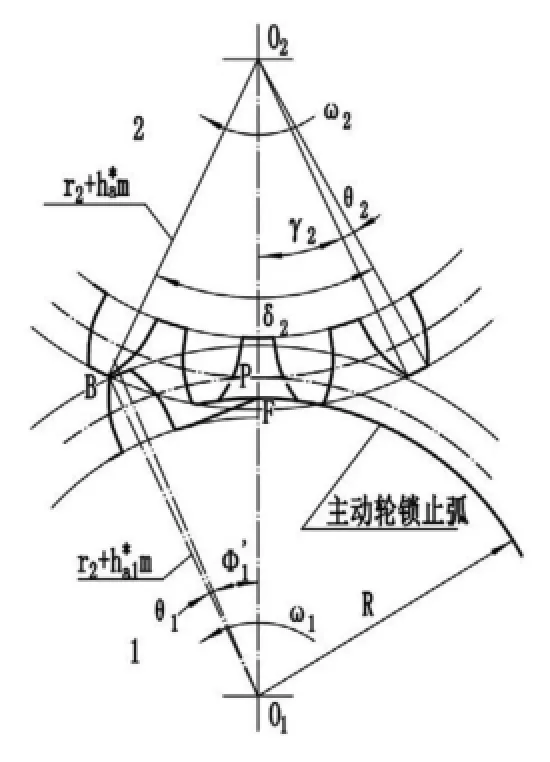
图3 主动轮锁止弧起点F的确定
如图3所示,主动轮锁止弧半径必须与从动轮锁止弧半径R相等,主动轮锁止弧起点的位置由角φ1’及半径R确定。
主动轮末齿齿顶圆压力角α"a1=arccos[(z1cosα)/(z1+2h*a1'')]=22.43°。
主动轮末齿齿顶圆齿厚所对中心角之半 θ1=[π/(2z1)]-(invα"a1-invα)=0.02632rad=1.5°。

2.2.3主动轮锁止弧终点的确定

图4 主动轮锁止弧终点G的确定
如图4所示,由角φ1和锁止弧半径R可确定主动轮锁止弧终点G的位置。
由于γ2+θ2=8.38° ,αa2-α=5. 56°,γ2+θ2>αa2-α,故主动轮首齿中心线与过锁止弧终点的半径间夹角φ1=arcsin{(z2+2)sin (γ2+θ2)÷)+ (z1+z2)2-2(z2+2)(z1+z2)cos(γ2+θ2}+π 2z1-invαA+invα=0.19443rad=11.14°
式中,αA为当开始啮合点不在啮合直线上(在从动轮顶圆上)时,主动轮首齿齿廓在啮合点处的压力角。
αA=arccos{z1cosα÷-2(z2+2)(z1+z2)cos(γ2+θ2)]}=16.74°
3 虚拟样机建立
按照上述计算得到的参数,在CAXA中建立主动轮和从动轮的齿廓曲线,将齿廓曲线导入UG中,分别建立主动轮和从动轮的三维模型,把不完全齿轮机构装配到一起,设置好初始位置,然后保存为parasolid格式,导入动力学仿真软件ADAMS中,添加约束,以此来完成虚拟样机的建立,见图5。

图5 不完全齿轮机构虚拟样机
4 虚拟样机仿真与分析
设置主动轮角速度为 2πrad/s,即360°/s,仿真步数step=30000,仿真时间为4s。
4.1从动轮的运动学理论参数
主动轮回转一周的时间为:
T=2π/ω=1s
从动轮每次转过的齿数:
z2’=ψ2z2/360°=12
主动轮上两锁止弧间的实际齿数:
z1’=z2’-K+1=10
主动轮首末两齿中心线间夹角:
ζ=2π(z1’-1)/z1=1.1781rad=67.5°
从动轮每一次运动的时间:
tf=T(φ1+ζ+φ1’)/2π=0.254s
从动轮每一次停歇的时间:
td=T-tf=0.746s
可得该机构的动停比为k=tf/td=0.34
4.2仿真结果分析
从动轮的角速度仿真结果见图6,在虚拟样机中,从动轮每一次运动的时间tf=0.28-0.02=0.26s,从动轮每一次停歇时间td=1.02-0.28=0.74s,可得在虚拟样机中的动停比为k=0.35,与理论计算结果基本一致,说明三维模型建立合理,该机构满足设计要求。

图6 从动轮角速度运动曲线
从图中还可看出,从动轮在每次运动的开始时刻冲击较大,表明不完全齿轮机构一般只适用于低速、轻载的场合。
5 结语
分析了不完全齿轮机构的运动特性,建立了不完全齿轮机构主动轮和从动轮的三维模型,在ADAMS中构造了不完全齿轮机构的虚拟样机,并对机构运动进行了仿真分析,通过仿真结果与理论分析的对比,验证了模型构建和理论分析的合理性,并且证明不完全齿轮一般只适用于低速、轻载的场合。
[1]邹慧君,殷鸿梁.间歇运动机构设计与应用创新[M].北京:机械工业出版社,2008.10.
[2]范成建,熊光明,周明飞.虚拟样机软件MSC.ADAMS应用与提高 [M].北京:机械工业出版社,2006.8.
[3]李增刚.ADAMS入门详解与实例[M].北京:国防工业出版社,2006.4.
[4]李宇庭,胡万里,谢伟华等.椭圆齿轮——槽轮组合机构的虚拟样机设计及仿真分析 [J].包装工程,2014-9(17):79-85.
田野,1990年出生,山西忻州人,硕士研究生,研究方向:武器结构设计及机械动力学。

