3-PSP并联机构雅克比矩阵及刚度分析
山西中北大学机械与动力工程学院 王明亚 李瑞琴 随磊
3-PSP并联机构雅克比矩阵及刚度分析
山西中北大学机械与动力工程学院王明亚李瑞琴随磊
本文研究了3-PSP并联机构的运动学逆解及雅克比矩阵,并求解了该机构的刚度矩阵模型。首先对机构进行描述,建立相应坐标系;利用闭环矢量法得到该机构的逆解约束方程;对约束方程求导,可得其速度雅克比矩阵;以雅克比矩阵为基础求解其刚度矩阵。
3-PSP;运动学逆解;雅克比矩阵;刚度
前言
少自由度并联机构近些年来成为机构学的研究热点。3-PSP空间并联机构是少自由度并联机构的一类,具有少自由度并联机构的传统优点,并有其独特性,目前研究和开发得还很不充分。邓飞等[1]建立了3-PSP空间并联机构的模型,得到了该并联机构位置正解方程,得出了其位置关系解。利用ADAMS对其进行了仿真分析,验证了位置计算方程的正确性。黄鹏等[2]建立了3-PSP机构运动学模型,进行了包括伴生运动和被动关节变量的完整运动学求解。对3-PSP机构的关节行程、速度特性和精度进行分析,证明该机构适用于混联结构中的并联模块,能够满足航空、航天、汽车等领域复杂零件的加工需要。张志良[3]对3-PSP并联机构行进了详细的运动性能研究,主要包括:机构奇异性、工作空间和灵巧度等,并进行了仿真,为3-PSP的研究奠定了基础。
本文首先对机构进行描述,建立相应坐标系;利用闭环矢量法得到该机构的逆解约束方程;对约束方程求导,可得其速度雅克比矩阵;以雅克比矩阵为基础求解其刚度矩阵。
1 3-PSP并联机构的描述与运动学逆解
1.1机构描述
3-PSP并联机构示意图如图1所示,3-PSP并联机构由动平台、静平台和三条PSP支链组成。动平台与静平台由相隔120°的三条支链连接,每条支链由一个驱动移动副(P)、一个被动球面副(S)和一个被动移动副(P)构成。如图1所示,在静平台上建立绝对坐标系{A-xyz};在动平台上建立坐标系{P-wuv}。
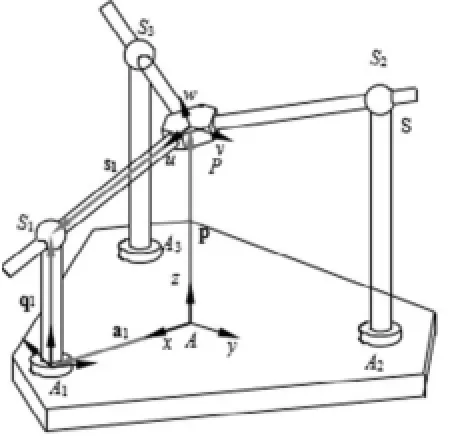
图1 3-PSP并联机构示意图
1.2机构运动学逆解
由图1可知,坐标系{A-xyz}中,设支链底A1、A2、A3为顶点的等边三角形的边长为a,则A到点A1、A2、A3的各矢量为:

坐标系 {P-wuv}中,设动平台中心P到球面副中心Si(i=1,2,3)的距离为bi,则各矢量为:

坐标系{A-xyz}中,到对应支链球面副中心Si的矢量,即三条支链驱动杆的长度:

设动平台中心点P的矢量为:

不同坐标系之间的矢量变换可以通过旋转矩阵进行转换[4]。利用旋转矩阵ApR,可以将坐标系{P-uvw}中任意矢量转化到坐标系{A-xyz}中,ApR为:

式中,c为cos的简写,s为sin的简写,θ、φ、λ为坐标系{P-uvw}相对于坐标系{A-xyz}绕x、y、z的三个独立转角。
因此,坐标系{A-xyz}中,动平台中心点P到球面副中心Si的矢量为:

使用封闭矢量环法,每条支链都可以得到一条闭环矢量[5]:

将式(6)代入式(7),可得该机构的运动约束方程:

求解式(8),式中共13个变量,θ、φ、λ为已知输出变量,a为机构参数,可求得三条支链驱动杆的长度qi。
2 雅克比矩阵分析
运动学逆解约束方程等式两边求导可得输入和输出速度之间的关系,可得机构的雅克比矩阵。
机构运动约束方程(8)对时间求导得:

式中,qi和bi分别为第i个驱动杆和球面副的运动速率和分别为第i个驱动杆和矢量si的单位向量,为动平台的第i条分支相对第i个球面副的运动速率,ω为动平台的旋转角速度,vp为P的速度
假设特定矢量n垂直于矢量si,其单位向量为:


根据向量运算性质得:

矩阵形式为:

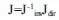
3 刚度矩阵
由于所研究的机构为对称机构,各分支的刚度系数之间存在如下关系k11=k22=k33,可以变形为。
4 结论
本文研究了3-PSP并联机构的运动学逆解及雅克比矩阵,并求解了该机构的刚度矩阵模型,为今后该机构在混联机构中应用提供了理论基础和参考依据。
[1]邓飞,李文忠.3-PSP并联机构的空间位置正解分析[J].机械设计,2009,26(1):41-45.
[2]黄鹏,王立平等.新型3自由度并联机构运动性能及精度分析[J].机械工程学报,2010,46(15):1-7.
[3]张志良.三自由度3-PSP并联机构运动性能与仿真研究[D].太原:中北大学,2014.
[4]黄真,赵永生,赵铁石.高等空间机构学[M].北京:高等教育出版社,2006.5.

