博弈论视角下的医保定点医疗机构监管分析
周良荣怀银平喻小倩李路路 朱 嵘
(1 湖南中医药大学管理与信息工程学院,长沙 410208;2 中和亚健康服务中心,北京 100000)
博弈论视角下的医保定点医疗机构监管分析
周良荣1怀银平1喻小倩1李路路1朱嵘2*
(1湖南中医药大学管理与信息工程学院,长沙410208;2中和亚健康服务中心,北京100000)
定点医疗机构和监管机构是对医保定点医疗机构进行监管所涉及的两个主体。而监管机构是政府的代表,对医疗机构监管不到位会导致医疗机构的一系列违规行为,最终导致社会利益受损。本文运用博弈论理论,构建和分析定点医疗机构和监管机构的博弈模型,指出降低监管成本、增加处罚罚金和增加医保带来的社会利益是决定医保定点医疗机构监管成果的三大最主要因素。
医疗保险;医疗监管;博弈
所谓医疗保险,是一种社会保障制度,就是指如果人们生病或者受伤,国家和社会会提供一种物质上(医疗服务或者经济补偿)的帮助[1]。在一定的程度上,医保制度能够正常的运行主要涉及了三个主体:患者、医疗机构和政府。患者是医疗行业中最弱势的群体[2],但同时也是最大的群体;政府是政策的制定者,能够保证患者的基本权益,追求最大化的社会利益;而医疗机构通常作为政府和患者的纽带,重视和关注患者,落实政府的政策,保障患者的基本卫生权利是它义不容辞的责任。然而,当前医疗市场已经形成,从全国来看,由于对定点医疗机构缺乏有效的监管机制的,一些医疗机构受利益的驱动,不仅仅没有按照要求操作,胡乱收费、乱开检查,而且不执行相关的规定,违规操作,套取资金,这些现象不仅存在,而且越发的严峻,医院追求自身利益最大化已经成为了事实[3]。不仅是严重危害了参保患者的利益,而且制约了医疗保障制度的可持续发展,对于定点医疗结构的有效监管已经愈发变得十分必要。而实际上,政府选择正确的策略与定点医疗机构之间进行博弈,是对定点医疗机构进行有效监管的关键所在。
1 博弈论的内涵
博弈论又被称为对策论,原来是运筹学上一个非常重要的分支,但是现在迅速发展,已经成为了备受关注的独立的学科,是一种关于决策和策略的理论[4]。博弈论主要用来研究当两个及以上的决策者之间存在相互作用,并且任何一个决策者的策略都不可能完全的独立于其他决策者的策略的时候,各个决策者的决策过程和均衡的问题。目前博弈论在政治、经济、法律、医疗、国家关系等许多个领域都有广泛的应用,它来源于一切通过制定策略进行合作和非合作的行为活动,同时也适用于一切需要进行决策的合作或非合作多行为活动,具有非常广泛大发展前景和应用前景[5]。
2 监管机构 (政府)与定点医疗机构的博弈模型分析
2.1模型假设假设1:存在两个博弈参与者:监管机构(政府)与定点医疗机构,他们都是“理性的经济人”,能够在已有的条件下追求实现自身利益的最大化[6]。其中,医疗机构是否违法依赖于违法所获得的利益以及被查出来后所需要付出的代价之间的权衡;监管机构是政府的代表,代替政府对医疗机构进行监督管理,保证医疗机构对行为合规合矩,保证医保政策带来的社会利益不受损害,但在保护社会利益进行监管的同时,需要付出一定的成本,因此,监管者需要在成本与获得的利益之间做出最佳权衡,做出最优决策;假设2:医疗机构通过乱收费、乱检查、套取资金等违规行为来获取额外收入,其策略有违规和守法两种,并假设医疗机构进行违规活动带来等额外收入为S(S>0),但是违规行为一旦被发现,则需要缴纳违规处罚金F(F>0),缴纳出罚金后医疗结果违规操作能够获取额外收入S-F;若医疗机构不进行违规操作,则不存在额外收入,即为0;假设3:监管机构可以通过对医疗机构是否存在违规行为进行监督检查,有检查和不检查两种策略。假设监管机构一旦进行检查就能够查出医疗机构对违规行为,但是需要付出检查成本C(C>0),如果医疗机构有违规行为,监管机构进行检查时,则会将对医疗机构进行处罚的罚金按b的比例转化成政府的收益,而最终收益是bF-C,如果不进行检查,收益为0,但是社会的利益会受到损害为-L;假设4:医疗机构与监管机构都是理性的经济人,都是为了追求自身利益的最大化。根据以上假设,可得到监管机构和医疗机构的博弈支付矩阵。(表1)
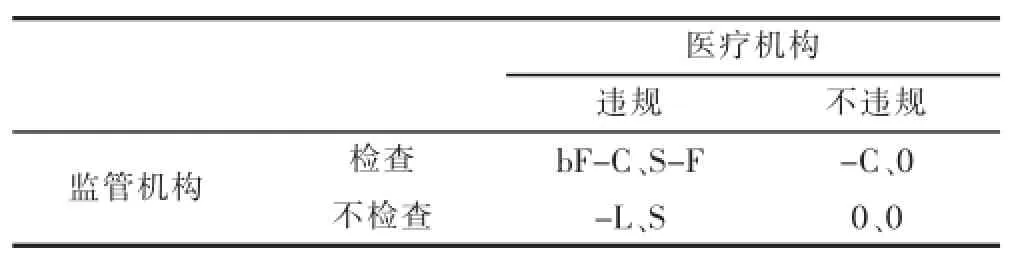
表1 医疗机构和监管机构的博弈支付矩阵
2.2均衡结果求解
2.2.1纯战略纳什均衡如果医疗机构不违规,监管机构则没有罚金收入,监管机构的最优决策是不进行检查,反之,如果医疗机构选择违规,当bF-C>-L时,即监管机构所获得的罚金收入大于损失的社会利益时,其最优的选择是检查,当bF-C≤-L时,即监管机构所获得的罚金收入小于等于所损失的社会利益时,其最优的选择是不检查;如果监管机构选择不检查,医疗机构则不会被扣除罚金,此时的最优选择时违规,而如果监管机构选择检查,当S-F>0时,即违规所获得的额外收入大于违规所被处罚打罚金时,定点医疗机构最优的选择是违规,当S-F≤0时,即违规所获得的额外收入小于等于违规所被处罚打罚金时,定点医疗机构最优的选择是不违规。因此,可以得出两个纯策略纳什均衡:(1)(违规,检查),此均衡出现的条件是bF-C>-L且S-F>0;(2)(违规,不检查),此均衡出现的条件是bF-C<-L,S-F>0或者S-F<0。
2.2.2混合战略纳什均衡当出现bF-C>-L且S-F<0时,即定点医疗机构选择违规时的额外收入小于它所收到的处罚,且监管机构进行监督检查时的所获得的罚金收益大于等于不进行监督检查时损失的社会利益时,就不存在战略纳什均衡,但是存在混合战略纳什均衡。
假定监管机构进行检查的概率是n,医疗机构违规操作的概率是m,监管机构通过选择“检查”和“不检查”两种策略使得定点医疗机构通过选择“违规”和“不违规”两种策略之间无差异,可得(bF-C)m-C(1-m)=-Lm。解得:m=C/(bF+L)
同样的,监管机构可以通过选择“检查”和“不检查”,使医疗机构在选择“违规”和“不违规”两种策略之间无差异,可得:(S-F)n+S(1-n)=0。可解得:n=S/F
由此,我们可以看到此博弈的纳什均衡为:S/F,C/(bF+L)],表示监管机构以S/F的概率进行监督检查,定点医疗机构以C/(bF+L)的概率进行违规行为。
2.3均衡结果分析根据以上分析,定点医疗机构进行违规操作所得到的额外收入S、被监管检查发现之后的处罚F、将罚金转化为监管机构的收入的比例b,监管机构进行监督检查时所付出的成本C,以及监督机构没有履行职责进行监管所损失的社会利益L,此5项因素为决定博弈均衡的关键。
监管机构选择n=S/F的概率进行监督检查,医疗机构选择m=C/(bF+L)的概率进行违规。当监管所需要的成本C变小时,医疗机构选择违规的概率也会减小,反之会增加;而当社会利益L、罚金F以及罚金转化成收入的比例变小时,医疗机构选择违规的概率m反而会上升,当罚金F增加时,医疗机构进行违规操作的成本会加大,当罚金大于其违规所获得的额外收益时,医疗机构会减少进行违规的概率,但同时,监管机构所获取的罚金收入减少,到止监管机构的进行监管的积极性降低,降低进行监管的概率;当违规所获得的收入S增大时,监管机构进行监督检查的积极性也会上升,进行监管的概率会随之增大。
3 结论
具体到实际中,降低监管成本,可以提高监管机构进行监管检查的积极性,从而减少定点医疗机构的违规行为;但是如果监管成本一直上升,监管机构需要付出高额成本,监管的概率将会下降,此时医疗机构则会选择违规行为的概率会增加。当医疗机构违规行为处以罚金时,势必会缩减医疗机构违规的额外收入,同时也将会降低医疗机构进行违规操作行为的概率。
根据以上分析,我们可以得到几点结论:(1)增加违规后的处罚罚金,提高处罚力度,能有效减少医疗机构的违规操作,但减少医疗机构的违规操作后,监管机构所获的额外收入随之减少,从而会影响监管机构监管的积极性;(2)降低监管成本是提高监管积极性、减少医疗机构违规操作行为的有效途径;(3)增加医保带来的社会利益将提高监管机构不进行监管的所付出的成本,最终也将督促监管机构进行监管。因此,在实际中,要充分重视监管成本、处罚力度以及医保带来的社会利益的重要作用,从中找到均衡点,不仅要提高监管机构的积极性,还要充分保证广大人民群众的社会利益。
以上博弈的基础是完全信息静态的博弈,双方都能充分了解信息,但现实中医疗机构与监管机构的博弈往往是动态的,且信息是不完全的。因此,以后的研究中需要进一步讨论,但以上分析仍然存在一定有效价值。
[1]温琳琳.论商业医疗保险与社会医疗保险的有机结合[J].中国乡镇企业会计,2012(7):237.
[2]孙庆文,钟飞等.博弈论在医疗卫生体制改革中的应用[J].中国医院管理,2002,22(7):4-6.
[3]王江辉.“定点医疗机构”监督管理中的难点及对策[J].新疆农垦经济,2007(2):62-65.
[4]许安拓.博弈论原理及其发展[J].人民论坛,2012(32):6-8.
[5]李绍奎,杨金侠,秦侠,等.博弈论在新型农村合作医疗中的应用[J].中国卫生经济,2008,27(3):50-52.
[6]张乐,李士雪,等.博弈论视角下的新型农村合作医疗定点医疗机构监管分析[J].中国初级卫生保健,2011,25(1):28-29.
Supervlslon Analysls of Deslgnated Medlcal lnstltutlons whlch Support Soclal Health Lnsurance ln the Perspectlve of Game Theory
ZHOU Liangrong1, HUAI Yinping1, YU Xiaoqian1, LI Lu1u1, ZHU Rong2
(1. Schoo1 of Information Techno1ogy and Management, Hunan University of Chinese Medicine, Changsha 410208, China;
2. Zhonghe Sub-hea1th Service Center, Beijing 100000, China)
Designated medica1 institutions and suPervision institutions are two main bodies which suPervise designated medica1 institutions suPPorting socia1 hea1th insurance.SuPervision institutions are the rePresentative of the government.The 1ess suPervision of medica1 institutions wi11 1ead to a series of i11ega1 behavior,and u1timate1y resu1t in damage to socia1 interests.This PaPer made use of game theory to construct and ana1yze the game theory mode of designated medica1 institutions and suPervision institutions,and Pointed out that reducing suPervising cost,increasing fines and socia1 benefits of hea1th care are the three major factors which can decide the regu1atory resu1t of designated medica1 institutions suPPorting socia1 hea1th insurance.
medica1 insurance;medica1 regu1ation;game theory
10.3969/j.issn.1672-2779.2016.03.016
1672-2779(2016)-03-0034-03
zhurong0008@139.com
(本文编辑:李海燕本文校对:喻小倩2015-11-11)

