基于地平仪的惯性-天文组合导航

王献忠，张　肖，张丽敏

(上海航天控制技术研究所/上海市空间智能控制技术重点实验室，上海　201109)



基于地平仪的惯性-天文组合导航

王献忠，张肖，张丽敏

(上海航天控制技术研究所/上海市空间智能控制技术重点实验室，上海201109)

针对惯性导航由于加速度计存在漂移不能长时间使用，以及传统滤波算法复杂不适合工程应用等问题，提出一种基于星敏感器与地平仪确定的地心指向偏差修正惯导输出的惯性天文组合导航算法，阐述了算法原理及实现过程，并分析了工程应用方式。最后通过仿真实验证明该方法可以抑制惯性导航累积误差，且算法简单、易于工程实现。

惯性导航；天文导航；星敏感器；地平仪；卫星

0　引言

惯性导航技术(以下简称惯导)可以确定卫星在惯性空间的位置和速度；但加速度计存在漂移，惯导不能长时间使用。基于星敏感器与地平仪确定的地心指向偏差修正惯导输出的位置和速度，进行惯性-天文组合导航可以抑制惯导累积误差。

受地平仪测量精度限制，基于星敏感器与地平仪惯性-天文组合导航的精度远低于全球卫星导航系统(global navigation satellite system，GNSS)兼容机与惯导组合导航的精度，目前主要用于异常情况下为星敏感器提供粗精度轨道根数，在星上GNSS兼容机异常，且没有地面实时上注轨道根数情况下仍能基于星敏感器确定本体相对轨道系的姿态。

国内外学者对惯性-天文组合导航进行了广泛的研究，文献[1]同时利用天体的方位和高度观测信息，实现多星矢量天文定位，但该算法仅适合地球表面应用。文献[2-6]均是采用星敏感器与地平仪信息作为观测量，但文献[2]基于模糊推理的自适应无迹卡尔曼滤波(fuzzy unscented Kalman filter，FUKF)方法进行研究；文献[3]基于遗传算法进行再采样的月球探测器自主天文导航粒子滤波新方法研究；文献[4]采用改进的代价参考粒子滤波(cost reference particle filter，CRPF)方法进行研究；文献[5]进行了基于无迹粒子滤波方法(unscented particle filter，UPF)的研究，克服了标准的粒子滤波不考虑最新量测信息和无迹卡尔曼滤波(unscented Kalman filter，UKF)只能应用于噪声为高斯分布的不足；文献[6]对粒子滤波方法进一步改进，采用易抽样的重要性采样密度函数来得到一组带权子样，并用这一组带权子样来近似滤波分布的样本；但上述滤波方法均存在算法复杂、计算量大的问题，不适合工程应用。文献[7]采用星光折射角作为观测量，并采用UPF滤波方法进行导航算法的研究，一方面用于观测星光折射角的星光敏感器还处于研制阶段，且观测方程在建立时对大气模型精度要求较高，另一方面UPF滤波算法复杂，目前阶段还不适合在轨实际应用；文献[8]采用联邦滤波，同时用星光角距和星光折射角作为观测量，其中的星光折射角观测存在与文献[7]相同的问题，且联邦滤波算法复杂，也不适合当前在轨应用。另外文献在基于地平仪作为观测量进行仿真分析的过程中，大部分认为地平仪的测量误差为白噪声；但根据地平仪在轨数据分析实际测量误差为正弦波形式，不同的误差模型会影响天文导航的精度。

本文侧重于天文导航方法在工程上的应用研究，采用成熟单机星敏感器、地平仪测量信息作为观测量，且没有采用复杂的滤波方法，而是采用地心指向偏差修正惯导输出进行惯性-天文组合导航算法研究，推导了基于J2000惯性系的卫星惯导解算算法，并给出了基于位置/速度误差修正量的组合导航算法；接着基于星敏感器与地平仪地心指向偏差计算惯导位置误差，并对位置/速度误差修正量进行估计；最后进行工程应用方式分析和仿真验证。

1　基于J2000惯性系的卫星惯导解算算法

(1)

(2)

(3)

设加速度计坐标系到J2000惯性系的姿态转换矩阵为Aia，求得J2000惯性系下卫星比力加速度aa,i为

aa,i=Aia·aa,a。

(4)

式中aa,a为加速度计测得的加速度计坐标系下的加速度。

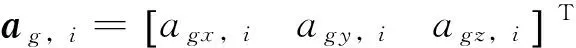
ai=ag,i+aa,i。

(5)

在J2000惯性系进行惯导解算位置ri/速度vi为：

(6)

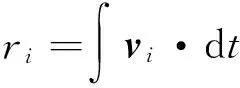
(7)

2　基于位置/速度误差修正量组合导航

结合式(6)和(7)惯导解算积分过程，在惯导积分过程中逐步增加位置/速度误差修正量，可以确保误差修正的平稳性。在J2000惯性系扣除位置/速度误差修正量，应用简化积分算法进行惯导解算的公式为：

(8)

(9)

式中：ai,k-1为第k—1步加速度；ai,k为第k步加速度；dvi,k-1为第k—1步估计的速度误差修正量；vi,k-1为第k—1步扣除速度误差修正量的速度；vi,k为第k步扣除速度误差修正量的速度；dri,k-1为第k—1步估计的位置误差修正量；ri,k-1为第k—1步扣除位置误差修正量的位置；ri,k为第k步扣除位置误差修正量的位置；T为导航解算周期。

3　基于星敏感器与地平仪计算惯导位置误差

3.1由位置/速度求qoi

(10)

(11)

(12)

h=r×v。

(13)

(14)

(15)

由Ω、i和u求得J2000惯性系到轨道系姿态4元数qoi为

qoi=q1⊗q2⊗q3⊗q4⊗q5。

(16)

3.2基于星敏感器与地平仪求地心指向偏差角

设星敏感器考虑曝光时差及数据采集延时修正并扣除安装矩阵后，得到星体相对J2000惯性系姿态4元数为qbi，结合轨道系相对J2000惯性系姿态4元数qoi求得本体相对轨道系姿态4元数qbo为

qbo=qoi-1⊗qbi。

(17)

其中qoi-1为4元数qoi的逆。

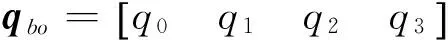
(18)

以欧拉角“312”转序(先绕Z轴转ψ，再绕X轴转φ，最后绕Y轴转θ)表示的转换矩阵为

(19)

式中：φ为滚动姿态角；θ为俯仰姿态角；ψ为偏航姿态角。

(20)

θ=0；

(21)

(22)

否则：

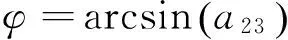
(23)

(24)

(25)

设地平仪在水平面内偏航安装角为ψH，将星敏感器求得的滚动和俯仰姿态转换到地平仪坐标系，得地平仪坐标系下滚动姿态角φ′和俯仰姿态角θ′为

(26)

式中ψ′=ψ+ψH。

设地平仪求得的滚动姿态角为φH，俯仰姿态角为θH，求得地平仪坐标系下滚动和俯仰姿态偏差为：

dφ′=φ′-φH；

(27)

dθ′=θ′-θH。

(28)

将地平仪坐标系下滚动和俯仰姿态偏差转换到轨道系，求得相对轨道系地心指向滚动偏差角dφ和俯仰偏差角dθ为

(29)

地平仪一般在水平面内正装，即ψH=0，稳态时3轴姿态角为小角度，地心指向偏差角可以近似解算为：

dφ=φ-φH；

(30)

dθ=θ-θH。

(31)

3.3基于地心指向误差角估计位置误差

相对轨道系地心指向滚动偏差角dφ、俯仰偏差角dθ、及轨道系下X向和Y向位置误差间的关系如图1所示。

图1　轨道系下位置误差与地心指向偏差惯性示意图

图1中地心距r由惯导解算输出，求得轨道系下X向和Y向位置误差为：

dx=r·dθ；

(32)

dy=-r·dφ。

(33)

(34)

因此可以基于dx估计dz，式(34)中dz基于dx采用比例估计为

dz=kpxz·dx。

(35)

式中kpxz为比例估计系数。

(36)

式中Aoi为惯性系到轨道系转换矩阵，可以类似式(18)由qoi求得。

4　估计位置/速度误差修正量

(37)

式中kp,r为位置误差修正量估计比例系数，是3×3对角阵，可以独立估计位置误差修正量。

(38)

(39)

(40)

式中kp,x、kp,y、kp,z为3轴位置误差修正量估计比例系数。

(41)

式中kp,v为速度误差修正量估计比例系数，是3×3对角阵，可以独立估计速度误差修正量。

(42)

(43)

(44)

式中kp,dx、kp,dy、kp,dz为3轴速度误差修正量估计比例系数。

5　工程应用方式及仿真验证

5.1工程应用方式

星敏感器与地平仪地心指向偏差可以获得2维位置误差，轨道系下Z向的位置误差利用X和Z之间耦合间接获取，其实时性不如直接获得3维位置误差的组合导航。

星敏感器定姿误差相对地平仪一般可以忽略，星敏感器与地平仪天文导航主要考虑地平仪定姿误差。地平仪姿态测量误差包括地球非球形误差、随季节变化的交变误差、观测噪声等，单扫描地平仪还包括升降轨交变误差。

为确保天文导航精度需要对地平仪姿态测量误差进行修正，在天文导航应用前基于地面测定轨或星上基于兼容机，包括全球定位系统(global positioning system，GPS)、格洛纳斯卫星导航系统(global navigation satellite system，GLONASS)的(GPS+GLONASS)组合导航定轨，用星敏感器输出的姿态修正地平仪测量误差，修正方式一般有2种：一种是基于误差模型修正，适用于双扫描或成像型精度较高的地平仪；另一种是查表修正，适用于单扫描等精度较差、误差规律不具有建模特性的地平仪。

星敏感器与地平仪地心指向偏差不直接反映速度偏差，且只有2维观测量，组合导航的实时性和修正性不如GNSS兼容机。

5.2仿真试验及结果分析

单圆锥扫描地平仪在轨测量误差约为0.25～1.00°，双圆锥扫描地平仪在轨测量误差约为0.05～0.07°，面阵地平仪在轨测量误差约为0.02～0.05°。

仿真时设置惯导用加速度计加速度常值漂移为1.0×10-3m/s2，忽略星敏感器测量误差，地平仪输出滚动和俯仰姿态常值偏差0.02°，按轨道周期正弦波动滚动姿态偏差幅值为0.02°，按半个轨道周期正弦波动俯仰姿态偏差幅值为0.02°；惯导积分周期0.4 s。

轨道系下位置误差仿真结果如图2所示，位置误差约5 km。

在轨对基于单扫描地平仪与星敏感器的惯性-天文导航进行了测试，并以兼容机为基准对天文导航误差进行评估。其中沿俯仰轴安装的地平仪在升降交点附近与星敏感器存在约0.5°的误差，由于地平仪测量误差是影响天文导航精度的主要因素，最终以GNSS兼容机定位数据为标称值的在轨天文导航位置误差约为30 km。具体测试曲线如图3所示。

图2　地平仪误差为正弦波情况下惯导-天文组合导航位置误差曲线

图3　惯性-天文组合导航在轨位置曲线

6　结束语

本文对基于星敏感器与地平仪惯性-天文组合导航算法进行研究，推导了基于J2000惯性系的卫星惯导解算算法，并给出了基于位置/速度误差修正量的组合导航算法；接着基于星敏感器与地平仪地心指向偏差计算惯导位置误差，并对位置/速度误差修正量进行估计；最后仿真验证了组合导航算法的有效性。本文采用成熟单机测量信息作为观测量，组合导航算法简单，且易于工程实现，并已通过在轨考核验证。

[1]李崇辉，李铸洋，郑勇，等.利用多星矢量观测信息进行天文导航定位技术的研究[J].导航定位学报，2013，1(3)：62-65.

[2]张迎春，李璟璟，吴丽娜，等.模糊自适应无迹卡尔曼滤波方法用于天文导航[J].哈尔滨工业大学学报，2012，44(1)：12-16.

[3]房建成，宁晓琳.月球探测器天文导航的遗传粒子滤波方法[J].北京航空航天大学学报，2006，32(11)：1273-1276.

[4]董唯光，李言俊，张科.改进的CRPF在自主天文导航中的应用[J].计算机测量与控制，2008，16(11)：1682-1684，1688.

[5]宋利芳，房建成.基于UPF的航天器自主天文导航方法[J].航天控制，2005，23(6)：31-34.

[6]LIU J，CHEN R.Sequential Monte Carlo methods for dynamic systems[J].Journal of American Statistical Association，1998，93(443)：1031-1041.

[7]张瑜，房建成.基于Unscented卡尔曼滤波器的卫星自主天文导航研究[J].宇航学报，2003，24(6)：646-650.

[8]王鹏，张迎春.基于信息融合的自主天文导航方法[J].系统工程与电子技术，2012，34(5)：1001-1006.

Inertial and celestial integrated navigation with horizon sensor

WANG Xianzhong，ZHANG Xiao，ZHANG Limin

(Shanghai Aerospace Control Technology Institute/Shanghai Key Laboratory of Aerospace Intelligent Control Technology，Shanghai 201109，China)

Aiming at the problem that the inertial navigation could not be used for a long time because of the accelerometer drift，and traditional filtering methods are complex and not suitable for engineering application，the paper proposed a method of the inertial and celestial integrated navigation based on the geocentric point error determined by star sensor and horizon sensor，which corrected the accumulative error of the inertial navigation system.The methods of the inertial and celestial integrated navigation and the algorithm process were discussed，and the engineering application mode was analyzed.Finally，the simulation results showed that the proposed algorithm could restrain the accumulative error of inertial navigation system with simple calculation and easy implementation.

inertial navigation；celestial navigation；star sensor；horizon sensor；satellite

2015-12-15

王献忠(1971—)，男，江苏太仓人，博士，研究员，研究方向为飞行器GNC系统研究与设计。

简介：张肖(1981—)，女，浙江舟山人，硕士，高级工程师，研究方向为飞行器姿态确定与控制研究与设计。

10.16547/j.cnki.10-1096.20160306.

P228

A

2095-4999(2016)03-0026-05

引文格式：王献忠，张肖，张丽敏.基于地平仪的惯性-天文组合导航[J].导航定位学报，2016，4(3)：26-30.(WANG Xianzhong，ZHANG Xiao，ZHANG Limin.Inertial and celestial integrated navigation with horizon sensor[J].Journal of Navigation and Positioning，2016，4(3)：26-30.)