一种适用于GPS /BDS多天线姿态测量的平差方法

张　康，郝金明，叶险峰，王兵浩，邓　柯

(1.1.北京卫星导航中心，北京　100094；2.信息工程大学 导航与空天目标工程学院，河南 郑州　450001；3.湘潭大学 能源工程学院，湖南 湘潭　411100)



一种适用于GPS /BDS多天线姿态测量的平差方法

张康1，郝金明2，叶险峰3，王兵浩2，邓柯2

(1.1.北京卫星导航中心，北京100094；2.信息工程大学 导航与空天目标工程学院，河南 郑州450001；3.湘潭大学 能源工程学院，湖南 湘潭411100)

为了提高GNSS姿态测量系统的精度和可靠性，提出一种适用于多天线姿态测量的3维无约束平差方法：通过一组基于4天线构型的GPS/BDS多频单历元静态实验，将所有的基线作为观测量整体进行3维无约束平差；并将平差前后的基线结果与利用平差前后的基线进行姿态角解算的结果分别进行对比。实验结果表明，在基于4天线构型的姿态角解算过程中，不论GPS还是BDS，使用这种平差方法都可使精度和可靠性指标有所提高。

卫星导航系统；姿态角结算；4天线构型；3维无约束平差

(1.Beijing Satellite Navigation Center,Beijing 100094,China；2.College of Navigation and Aerospace Engineering,Information Engineering University, Zhengzhou，Henan 450001,China;3.Energy Engineering College of Xiangtan University，Xiangtan，Hunan 411100,China)

0　引言

当前，中国的北斗卫星导航系统(BeiDou navigation satellite system，BDS)和美国的全球定位系统(global positioning system，GPS)一样不仅能提供精确的定位、导航、授时信息，还能提供载体的速度、姿态、定向信息。在工程测量和武器装备的使用上，姿态测量都是基础性的工作。与传统的惯性器件相比较，基于全球卫星导航系统(global navigation satellite system，GNSS)的姿态测量系统具有成本低和误差无积累等优点，已被广泛应用于塔吊、桥梁、工程车辆等的实时姿态监控过程中，在节约了大量人力的同时也保证了作业的安全性。当前，基于GNSS的姿态测量研究已经取得了丰硕的成果[1-2]，研究重点主要集中在姿态测量的精度和可靠性方面[3]。

原则上，利用3台不共线的天线构成的2条独立基线就能够确定姿态角。基于4天线构型的姿态角解算过程若只解算2条独立基线，可以提高姿态角的输出频率；但会造成冗余信息的缺失，使得姿态角解算精度和可靠性没有保证[4]。如果将所有基线进行求解，然后将冗余基线与其他2条基线作为观测量整体平差，就可以改善姿态角的精度和可靠性[4-5]。

本文通过基于4天线构型的GPS/BDS多频单历元静态实验，分别针对GPS和BDS的基线解算结果进行整体平差，由于缺少必要的起算数据，所以选择3维无约束平差方法。本文通过对比分析GPS和BDS平差前后的基线结果与利用平差前后的基线进行姿态角解算的结果来进行研究。

1　GNSS姿态测量数学模型

利用固定在载体上的不少于2个GNSS天线，通过载波相位差分精确确定天线之间的相对位置，就可以利用解算出来的基线向量来确定载体的3个姿态角：偏航角Ψ、俯仰角θ和横滚角φ(通常称之为直接法[6-7])。

通常，我们假设2个天线A、B沿载体的主轴方向放置，那么通过主基线AB就可以确定载体的偏航角Ψ和俯仰角θ[5]。

通过求解载波相位整周模糊度，2个天线A、B在地心地固坐标系中的相对位置dXEE可以精确求得；根据地心地固坐标系到当地水平坐标系的转换关系，即可获得天线A、B在当地水平坐标系下的相对位置

(1)

天线A、B在当地水平坐标系下的相对位置dXLL与其在载体坐标系内的基线向量dXB的关系为

dXLL=R3,1,2(Ψ,-θ,-φ)dXB。

(2)

式中R3,1,2(Ψ,-θ,-φ)为姿态矩阵，可以表示为

(3)

那么就可以确定主基线AB的2个姿态角[4]为

(4)

式中 Ψ和θ分别为载体的偏航角和俯仰角。

当第3个天线C与天线A组成一条新的基线AC(需要注意的是3个天线不能共线)，那么第3个姿态角φ可以求解。为了使姿态角解算精度更高，一般将2条基线进行正交放置[4,6]。

(5)

则载体的第3个姿态角即载体的横滚角就可以确定，表示为

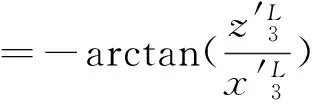
(6)

2　GNSS基线网平差数学模型

2.1误差方程

GNSS网3维无约束平差所采用的观测值为基线向量，也就是GNSS基线向量的起点到终点的坐标差。

假设任一天线i的空间直角坐标值为参数，那么有

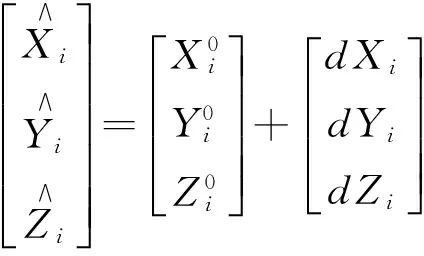
(7)

在对于每一条基线，都可以列出一组误差方程为

(8)

假定第m1条基线向量是由第n1点(起点)指向第n2点(终点)，总的误差方程可以表示为

(9)

2.2秩亏自由网基准

GNSS基线向量(坐标差)网平差中，R(A)=t-3=3n-3，秩亏数d=3，引入基准方程[3，7]如下：

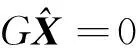
(10)

2.3观测值权阵

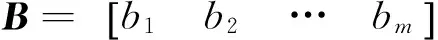
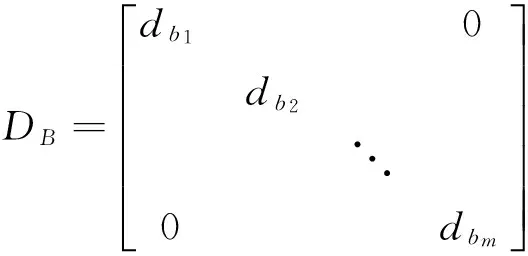
(11)

(12)

则基线向量观测值权阵可以表示为

(13)

2.4方程的解

联合式(9)、式(10)和式(13)，按照最小二乘原理进行平差解算得到平差结果，可以表示为

(14)

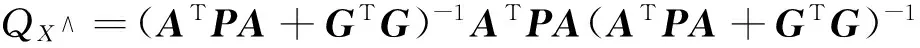
(15)

(16)

3　实验与结果分析

为了对本文提出的平差方法进行验证，于2015-10-27利用4台司南M300 Pro多系统多频接收机进行了相关的实验，实验数据在信息工程大学GNSS实验场采集，数据采样率为1 s，高度角截止角设置为15°。实验过程中4个GNSS天线A、B、C、D按照如图1所示配置，均采用4天线之间相邻两两直角分布，其中以AB为主基线。实验共采集4个时段静态观测数据，分别设置了4组不同基线长度(主基线AB长度分别约为0.8、2.4、6 m和10 m)的实验，各时段历时约40 min。

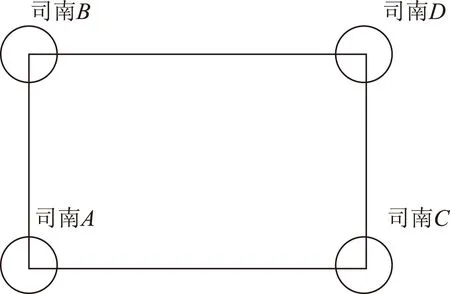
图1　天线分布示意图

本文分别对4组不同基线长度的静态实验中的所有4台接收机采集的GPS及BDS系统多频数据进行单历元基线解算，采用LAMBDA算法和单历元整周模糊度固定策略来求解模糊度[7]，设置模糊度固定的RATIO限值为3.0。由于本文解算的是超短基线，因而数据处理时对流层及电离层改正基本可以忽略，星历均采用广播星历。然后将同一时刻6条基线解利用本文提出的3维无约束平差得到对应基线平差结果。最后将直接通过基线结果进行姿态解算与通过基线平差结果进行姿态解算的结果进行对比。由于篇幅限制，下文中仅以主基线长度约为2.4 m的静态实验处理结果为例做出分析。

3.1基线平差结果分析

在主基线长度约为2.4 m的静态实验中，GPS系统的共视卫星数目往往在8颗左右，而北斗系统共视卫星数目往往在9颗左右。不论是GPS还是BDS，它们得到所有6条基线的解算成功率都能达到99.5 %以上。

对于GPS及BDS，分别将其所有基线结果进行3维无约束平差，平差前后基线东、北、天顶方向(E、N、U方向)结果的对比情况如图2至图5所示。

从图2至图5可以看出，不论GPS还是BDS，它们的基线解算结果经过平差后在结果稳定性方面均要优于直接解算的结果。

平差前后，GPS/BDS基线东、北、天顶方向(E、N、U方向)结果的标准差STD统计见表1。

对比表1中BDS与GPS解算的基线结果，不论是平差前还是平差后，它们的精度基本在同一水平；但是在U方向BDS的解算结果优于GPS，原因是由于GPS系统本身在高程方向的精度略差[6]。

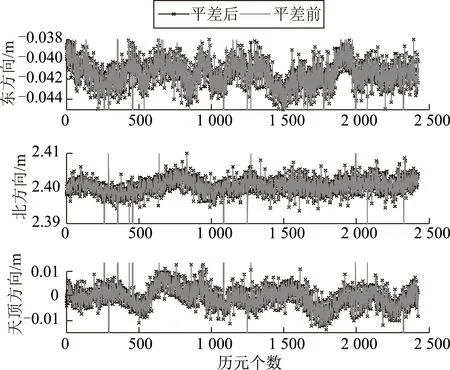
图2　基线平差前后结果对比(GPS)

图3　基线平差前后结果对比(GPS)

图4　基线平差前后结果对比(BDS)

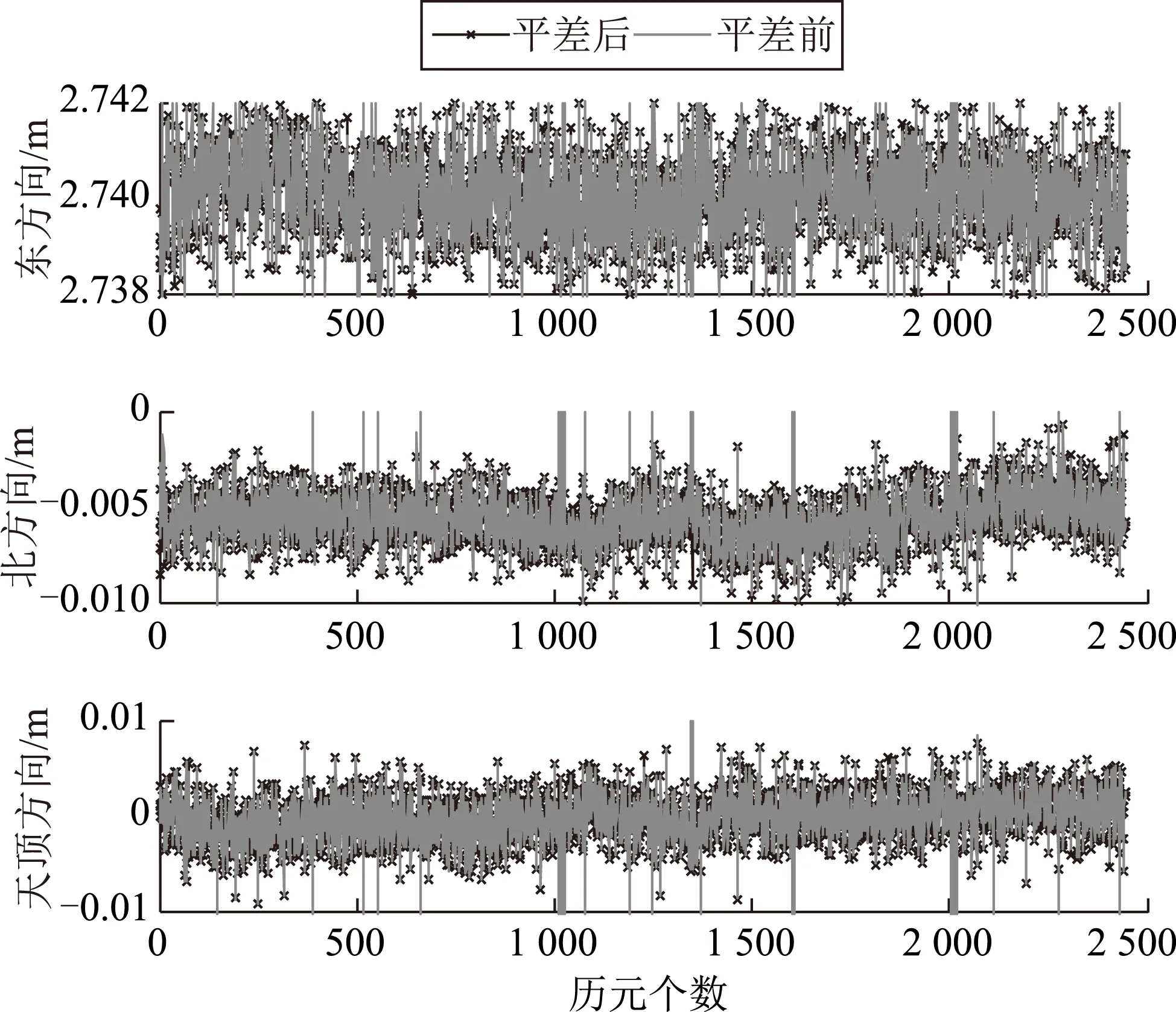
图5　基线平差前后结果对比(BDS)

从表1还可以看出，不论GPS还是BDS，其基线解经过平差后的标准差(STD)较平差之前的有接近50 %的减小，说明平差之后结果稳定性变好，这一结果将影响到之后的姿态角解算。

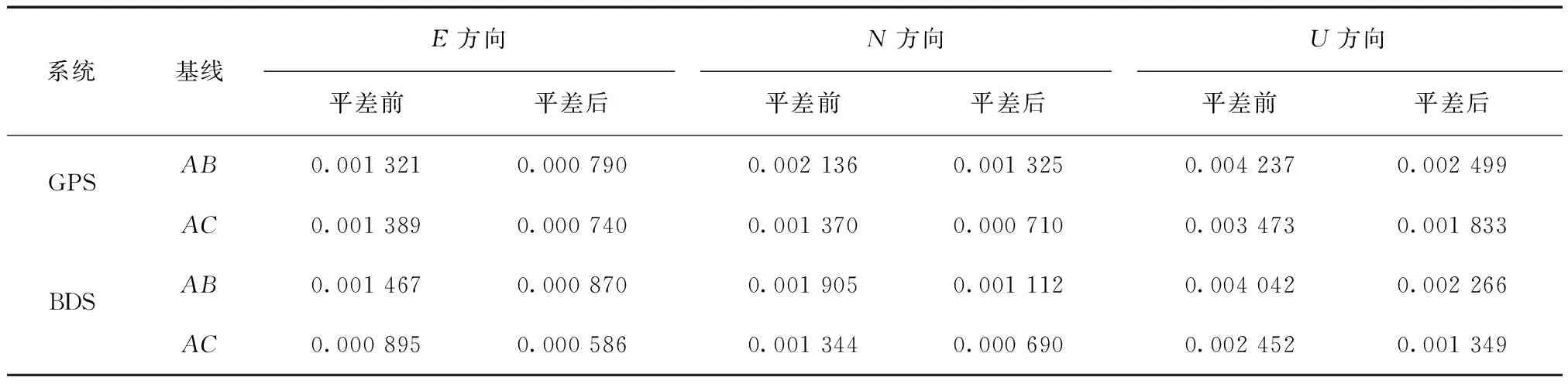
表1　GPS/BDS基线平差前后STD对比　m

3.2姿态解算结果分析

对于GPS及BDS，分别利用平差前后的基线结果通过GNSS姿态测量数学模型进行姿态角解算，基线解平差前后姿态解算结果的对比情况如图6至图7所示。

图6　GPS基线平差前后姿态解算结果对比

图7　BDS基线平差前后姿态解算结果对比

通过表 2可以看出，利用BDS和GPS进行姿态测量的结果精度在同一水平，验证了目前BDS的定位性能与GPS基本一致。

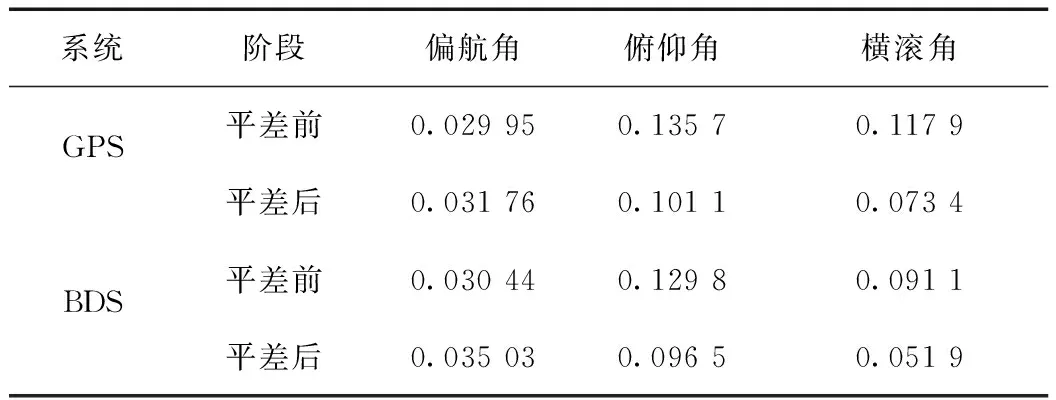
表2　GPS/BDS基线平差前后姿态角解算结果STD对比　(°)

从图6、图7和表 2中可以看出，对于2.4×2.4 m2的4天线正交布局姿态测量系统而言，不论是GPS还是BDS，基线网平差前偏航角的精度都能达到0.03°，俯仰角和横滚角精度略差在0.1°左右；经过基线3维无约束平差后，偏航角的精度提高得并不明显，而俯仰角和横滚角的精度有了较大的提高：由此可见，将基线测量结果进行平差可以提高姿态角解算精度，使结果精度更加均衡。

将GNSS观测基线结果整体进行3维无约束平差后，实质上是将总体误差更加合理地分摊到东、北、天顶(E、N、U)3个方向上，使3个姿态角的精度更加均衡。

4　结束语

本文对适用于GPS/BDS多天线姿态测量的平差方法进行了相关研究，通过实测数据解算和结果分析，初步得到了以下结论：

1)本文提出的先将GPS/BDS观测基线结果作为整体进行3维无约束平差，再利用平差后的基线结果进行姿态解算的思路，能够有效地提高姿态角输出的精度和可靠性。

2)利用BDS与GPS进行基线解算，不论是平差前还是平差后，BDS与GPS的精度基本在同一水平，但是在天顶方向BDS的解算结果优于GPS。

3)利用BDS和GPS进行姿态测量，结果精度在同一水平，验证了目前BDS的定位性能与GPS基本一致。

4)不论GPS还是BDS，其基线解经过平差之后结果稳定性更好，平差后基线东、北、天 3个方向标准差(STD)较平差之前减小了近50%。

5)不论GPS还是BDS，其基线解经过平差之后再进行姿态解算，结果偏航角的精度提高得并不明显，而俯仰角和横滚角的精度有了较大的提高。

[1]TEUNISSEN P J G，GIORGI G，BUIST P J.Testing of a new single-frequency GNSS carrier phase attitude determination method：land，ship and aircraft experiments[J].GPS Solutions，2011，15(1)：15-28.

[2]李俊毅.GPS 姿态测量及相关技术的研究[D].郑州：信息工程大学，2004：54-67.

[3]李征航，黄劲松.GPS测量与数据处理[M].武汉：武汉大学出版社，2010：289-312.

[4]KUYLEN L V，BOON F，SIMSKY A.Attitude determination methods used in the PolaRx2@ multi-antenna GPS receiver[C]//The Institute of Navigation(ION).Proceedings of the 18th International Technical Meeting of the Satellite Division of the Institute of Navigation.California：ION，2005：125-135.

[5]WANG B，MIAO L，WANG S，et al.A constrained LAMBDA method for GPS attitude determination[J].GPS Solutions，2009，13(2)：97-107.

[6]王兵浩.BDS/GPS姿态测量方法研究[D].郑州：信息工程大学，2015：45-56.

[7]隋立芬，宋力杰，柴洪洲.误差理论与测量平差基础[M].郑州：测绘出版社，2010：185-190.

[8]刘基余.GPS卫星导航定位原理与方法[M].北京：科学出版社，2008：300-312.

[9]刘若普.GPS三维姿态测量技术研究[D].上海：上海交通大学，2007：33-46.

[10]张前勇，汪雷.GPS高程测量精度分析[J].湖北民族学院学报：自然科学版，2008，26(4)：422-425.

[11]GIORGI G，TEUNISSEN P J G，BUIST P J.A search and shrink approach for the baseline constrained LAMBDA method：experimental results[C]//Tokyo University of Marine Science and Technology Laboratory of Satellite Navigation.Proceedings of the International Symposium on GPS/GNSS.Tokyo，Japan：Curran Associates，Inc.，2009：797-806.

[12]TEUNISSEN P J G.The least-squares ambiguity decorrelation adjustment：a method for fast GPS integer ambiguity estimation[J].Journal of Geodesy，1995，70(1/2)：65-82.

[13]王冰，隋立芬，张清华，等.利用GPS解算载体测姿的算法研究[J].武汉大学学报·信息科学版，2013，38(12)：1392-1395.

An adjustment method suitable for GPS/BDS multi-antenna attitude determination

ZHANG Kang1，HAO Jinming2，YE Xianfeng3，WANG Binghao2，DENG Ke2

In order to improve the accuracy and reliability of GNSS attitude measurement system，the paper proposed a three-dimensional non-constrained adjustment method for multi-antenna attitude measurement：through the GPS/BDS multi-frequency single-epoch static test based on the four-antenna configuration，all the baselines was taken as the whole concept of measuring to be adjusted by the three-dimensional non-constrained adjustment； and the final results of the baseline before or after adjustment and the attitude angles solved by both baseline results before or after adjustment were compared respectively.Result showed that using the adjustment method for the attitude determination of both BDS and GPS based on four-antenna configuration，the accuracy and reliability could be improved efficiently.

satellite navigation system； attitude determination； four-antenna configuration； three-dimensional non-constrained adjustment

2015-11-04

湖南省教育厅资助科研项目(13C903)；地理信息工程国家重点实验室重点基金课题“面向无人机自主着陆的卫星/惯性/视觉信息融合研究(SKLGIE2014-Z-2-1)。

张康(1990—)，男，福建莆田人，助理工程师，研究方向为精密相对定位与姿态测量。

10.16547/j.cnki.10-1096.20160313.

P228.4

A

2095-4999(2016)03-0058-06

引文格式：张康，郝金明，叶险峰，等.一种适用于GPS/BDS多天线姿态测量的平差方法[J].导航定位学报，2016，4(3)：58-63.(ZHANG Kang，HAO Jinming，YE Xianfeng，et al.An adjustment method suitable for GPS/BDS multi-antenna attitude determination[J].Journal of Navigation and Positioning，2016，4(3)：58-63.)