求解两体问题数值方法的创新性研究

郝海玲

(晋中职业技术学院　基础部，山西省　晋中市　030600)



求解两体问题数值方法的创新性研究

郝海玲

(晋中职业技术学院基础部，山西省晋中市030600)

该文阐述了求解两体问题的线性对称多步数值方法——Obrechkoff法。N体问题是一个很难的问题，只有少数微分方程存在解析解，近似方法是解微分方程的主要手段，高精度的轨道问题需要长时间的数值积分。因此，选用线性对称多步方法，在其主结构上增加高阶微商，不仅有理想的精度和较好的稳定性，而且可以大大减少截断误差，尤其在很大程度上减小了误差系数。研究表明，该方法求解两体问题的数值解具有高精度、高效率及稳定性好的优点。

P稳定；两体问题；高阶微商；截断误差

N体问题是一个很难的问题，高精度的轨道问题需要长时间的数值积分。然而许多传统的数值方法，如Runge-Kutta法、Adams法、Euler法和Störmer-Cowell法等都不是很适用，因为这些方法都存在许多缺点。如它们的稳定区域很小，长时间的积分会使误差不断增加，精度也很难通过增加节点来提高。因此需要一种高精度、稳定性好的方法来解两体问题。三角拟合的对称多步法已经解决了很多问题[1-5]，所以采用Obrechkoff[6]多步方法来研究两体问题。其利用高阶微商来减少截断误差，很大程度上减小了误差系数[7]。

1　数值方法介绍

Obrechkoff方法是利用增加高阶微商来提高方法的精度。该方法在1942年被提出，但由于高阶微商的使用计算非常复杂，并且当时的计算机有所限制，所以没有得到广泛的应用。近年来由于计算机的计算功能不断提高，Obrechkoff方法已经被广泛应用。如薛定鄂方程或Duffing方程。这两种方法对线性多步方法增加高阶微商，高阶微商可以表示成一阶微商和二阶微商的线性组合。然而在计算过程中发现，一阶微商的公式的精度也影响着该数值方法的精度[8]。Obrechkoff方法的计算方程为：

(x-ih))+…

(1)

为了保证方法的稳定性，该方法的系数仍然通过三角拟合的方法。

O(h15)

(2)

可以看出四步方法的误差系数非常小，并且具有较高的精度。

O(h17)

(3)

(4)

通过比较截断误差的误差系数和h的阶数，发现增加高阶微商能够明显提高数值方法的精度，因此最后选择用Obrechkoff数值方法来计算两体问题。

2　Obrechkoff方法解两体问题

本文用Obrechkoff方法求解著名的两体问题[9]的数值解，为计算简便，其中一个质点的质量远远大于另一个质点，所以小质点的质量可以忽略不计，大质点的质量等于1，引力常数为1，根据万有引力定律，小质点的运动方程为：

-f(x(t),y(t))x(t)

(5)

-f(x(t),y(t))y(t)

(6)

显然式(5)、式(6)是非线性常微分方程。两体问题的解析解为：

(7)

其中，u和t的关系满足

u-ecos(u)-t=0

(8)

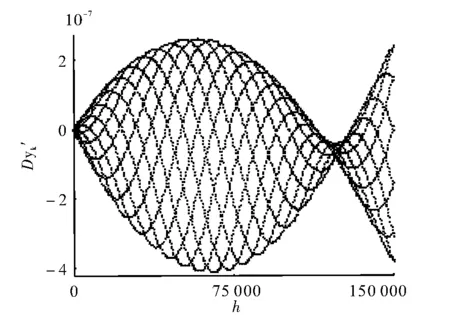
式中，u表示做椭圆运动的转动的角度，t表示时间，e表示偏心率(0

本文尝试用Obrechkoff方法的各种不同形式对两体问题进行了数值计算，希望能够提高数值解的精度，下面介绍多次计算，结果都比较理想。

P稳定四步方法的主要结构如下：

q0(h)=y(t+2h)+y(t-2h)+c0y(t)+

c1(y(t+h)+y(t-h))+h2[c2(y″(t+2h)+

y″(t-2h))+c3(y″(t+h)+y″(t-h))+

c4y″(t)]+h4[c5(y(4)(t+h)+y(4)(t-h))+

c6y(4)(t)]

(10)

图1　ω=1,e=0.1,h=0.1,t=100 000

本文还对四步高阶微商方法加上最外点，需要利用Newton线性化方法，虽然减少了误差，提高了精度，但是计算工作量非常复杂，对现在的计算机内存来说计算量过大，因此除了期待更加先进的计算机问世之外，我们还需要寻找更简便且精度较高的数值方法。因此，本文还运用了两步四阶微商对称方法进行了数值计算，得到的结果是最理想的，如图2所示。

图2　ω=1,e=0.1,h=0.1,t=150 000

而用八步线性对称方法得到了两体问题的数值解[3]，如图3所示。

图3　ω=1,e=0.1,h=0.1,t=100 000

通过对图1～图3进行比较，可以看出新的方法不仅精度更高且稳定性较好。在计算过程中发现，对于两体问题，当e<0.5时，该方法比较理想。当1>e>0.5时，该方法的误差就会随着时间的增加而增大。但是这种现象不是数值方法引起的，可以由它的物理意义，即开普勒第二定律来解释：行星和太阳之间的连线在相等的时间内所扫过的面积相等。质点的运动方程表明坐标中心取在椭圆焦点上，如图4所示。

图4　不同偏心率的椭圆

当经过相等的时间，e值大的椭圆较扁，并且右焦点离质点运动轨道很近，而e值小的椭圆，质点的轨道离焦点较远。因此，在相等的时间内，各个椭圆右焦点附近的质点的速度有很大的不同，运动质点在e值大的椭圆上速度较快，在e值小的椭圆上速度较慢，这样就表现为在e值大的轨道上运动的误差随时间的加长而有可能增加得更快。

3　结束语

这种新的P稳定Obrechkoff结构求解两体问题，目前达到了理想的精度和较好的稳定性，但还需进一步研究。若在稳定性良好且缩小步长的情况下能提高精度，那么该方法将可以运用到三体问题，从而为研究N体问题提供精度较高的数值方法，能够比较精确地了解天体中的某个星球经过长时间的运动后的运动情况，预知该星球是否会影响人们赖以生存的地球。

[1]WANGZhongcheng.Anewtrigonometrically-fittingtechniquetoconstructasymmetriclinearmulti-stepmethodforthenumericalsolutionofanorbitalproblem[J].NewAstronomy，2005, 11(2)：90-102.

[2]SIMOSTE.Exponentially-fittedandtrigonometrically-fittedmethodsforlong-termintegrationoforbitalproblems[J].NewAstronomy，2003, 8(5)：391-400.

[3]SIMOSTE.Exponentially-fittedandtrigonometrically-fittedmethodsforthenumericalsolutionoforbitalproblems[J].NewAstronomy，2003(8);391-400.

[4]SIMOSTE.Trigonometrically-fittedpartitionedmultistepmethodsfortheintegrationoforbitalproblems[J].NewAstronomy，2004, 9(6)：409-415.

[5]SIMOSTE.Dissipativetrigonometricallyfittedmethodsforthenumericalsolutionoforbitalproblems[J].NewAstronomy，2004, 9(1)：59-68.

[6]NAUKA.Obrechkoffn,onmechanicalquadrature(bulgarianfrenchsummary)[J].SpisanieBulgar，1942(65)：191-289.

[7]ZHAODeyin，WANGZhongcheng，DAIYongming.Importanceofthefirst-orderderivativeformulaintheObrechkoffmethod[J].ComputerPhysicsCommunications，2005, 167(2)：65-75.

[8]SIMOSTE.Ap-stablecompleteinphaseObrechkofftrigonometricfittedmethodforperiodicinitial-valueproblem[J].ProceedingsoftheRoyalSocietyA，1993, 441(1912)：283-289.

[9]PSIHOYIOSG，SIMOSTE.Trigonometrically-fittedsymmetricmultistepmethodsfortheapproximatesolutionoforbitalproblems[J] .NewAstronomy，1939, 14(2)：175-184.

[10]WANGZhongcheng.Trigonometrically-fittedmethodwithfourierfrequencyspectrumforundampedduffingequation[J].ComputerPhysicsCommunications，2006，175(4)：241-249.

Innovative Research of Obrechkoff Method for the Numerical Solution of Orbital Problems

HAO Hailing

(DepartmentofFoundation,JinzhongVocationalTechnicalCollege,Jinzhong030600,China)

WefocusonthenewkindofP-stableObrechkoffmethodforthenumericalsolutionoforbitalproblems.However,onlyafewofthesedifferentialequationscanbesolvedexactly.Approximatemethodsarethemainmeansforsolving,analyzingandunderstandingphysicsproblems.ThroughimprovingtheWang’smethod,wedevelopanewkindofP-stablefour-stepObrechkoffmethodbyaddingthehigher-orderderivatives.Thisproposedmethodisveryeffectivebuthasveryhighlocaltruncationerror.ThenumericalexperimentsforthenumericalsolutionoforbitalproblemshastheadvantageovertheWang’smethodinaccuracyandefficiency.

P-stable；orbitalproblem；higher-orderderivatives；localtruncationerror

2014-10-11；修改日期: 2016-06-22

郝海玲(1979-)，女，硕士，讲师，主要从事物理问题的数值解法方面的研究。

O411

Adoi:10.3969/j.issn.1672-4550.2016.04.014