基于Matlab的PID控制器参数整定方法

张　婧，盖文东，徐文尚，陈志巧

(山东科技大学　电气与自动化工程学院, 山东　青岛　266590)



基于Matlab的PID控制器参数整定方法

张婧，盖文东，徐文尚，陈志巧

(山东科技大学电气与自动化工程学院, 山东青岛266590)

针对教学中学生在面对PID控制器参数整定过程时存在的问题，在已知表征被控对象的某一传递函数基础上，基于自动控制原理的基础知识，利用Matlab自带的Rltool工具箱，该文提出一种简单易行的PID控制器参数整定方法。实践表明该方法调整参数方便，容易掌握，并有助于学生深化对采用时域法、根轨迹法和频域法分析与设计控制系统的理解。

比例-积分-微分控制器；参数整定；Matlab软件；根轨迹

自动控制原理和计算机控制技术是工科院校自动化专业重要的专业课程，其主要任务是通过控制理论的学习，了解系统的概念，掌握分析和设计控制系统的方法，培养学生解决实际工程问题的能力。在控制系统设计中最重要的一项内容就是控制规律设计，目前应用广泛的控制算法就是PID控制[1]。PID控制算法作为经典控制算法中的典型代表，它具有结构简单、参数物理意义明确、易于实现、鲁棒性好和可靠性高等优点[2]。然而PID控制算法的难点不是编写或阅读控制程序，而是整定控制器的参数[3]。在多年的教学实践中发现，学生可以理解和掌握PID控制算法的原理，但在课程设计、综合实验以及毕业设计中，面对一个实际的控制系统，却不知如何应用自动控制原理中的经典控制理论知识去设计一个满足控制要求的PID控制器。这就造成了自动控制原理的理论学习与实践应用的脱节，使学生认为自动控制原理的知识没有用处。目前，在我校本科教学过程中讲述的PID参数整定方法为简易工程法[4]，包括扩充临界比例度法、扩充响应曲线法、衰减曲线法、极限环自整定法和凑试法等，但这些整定方法与学生学习的自动控制理论知识相关性较小。

Matlab软件可用作动态系统的建模、分析和仿真，广泛应用于分析和辅助设计控制系统。采用Matlab仿真软件可分析和设计连续控制系统和计算机控制系统[5-7]，可以促进学生对控制理论知识的学习。

针对教学过程中PID控制器参数整定的难点，在已知表征被控对象的某一传递函数的基础上，基于自动控制原理的基础知识，利用Matlab自带的基于根轨迹分析的SISO系统设计工具箱Rltool(Matlab5.2版本及以上)，本文提出一种简单易行的PID参数整定方法，为学生采用PID控制器设计控制系统提供方便，且可进一步加深学生理论知识与实际应用的结合。

1　PID参数整定方法的理论基础

在论述PID控制器参数整定方法前，首先要理解时域、根轨迹和频域3种方法分析控制系统性能之间的内部关联。

时域分析法分析控制系统的稳定性、稳态性能和动态性能，实质上是在分析闭环控制系统的极点和零点对系统输出的影响；根轨迹分析法是根据控制系统开环零极点的位置以及可变参数根轨迹增益K*从0→∞变化时，求取闭环控制系统的极点在复平面s上的分布，从而分析系统的稳定性、稳态性能和动态性能；频域分析法是根据开环控制系统的开环对数频率特性曲线(Bode图)分析开环频域指标截止频率和相角裕度以及闭环频域指标带宽频率和谐振峰值，根据频域和时域性能指标的对应关系从而分析控制系统的稳定性、稳态性能和动态性能。

由此可见，时域、根轨迹和频域3种方法分析控制系统是相互关联的，决定控制系统性能的根本就是闭环极点，在设计PID控制器时，综合3种分析方法的特点，根据控制系统性能指标的要求调整PID控制器参数。

2　PID参数整定方法的实现

PID控制器的基本控制规律为比例+积分+微分控制，即将偏差的比例(P)、积分(I)和微分(D)通过线性组合构成控制量，对被控对象进行控制[2]，其模拟PID控制规律为：

或写成传递函数形式为：

(3)

式中，e(t)、E(s)、e(k)分别为偏差输入信号，u(t)、U(s)、u(k)分别为控制输出信号，Kp为比例系数，TI为积分时间常数，TD为微分时间常数，T为采样周期。

如果在控制系统中使用PID控制器，需要整定的主要参数有Kp、TI和TD。

2.1PID参数整定方法的实现

以机器人和视觉系统中的PID控制器参数整定方法的实现为例。

控制器参数整定方法由如下7个步骤实现。

1) 求取原系统采用零极点表示的开环传递函数G(s)=2/[(s+1)(s+2)]。

2) 在Matlab的Command Window中键入如下命令：

以上命令可打开“Control and Estimation Tools Manager”系统控制和估计工具管理器，以及如图1所示的原系统根轨迹。由于题目要求设计串联PID控制器，故选择默认的“Architecture”中的结构，C为PID控制器，F始终为1。

图1　基于Rltool的原系统根轨迹

3)在绘制开环控制系统根轨迹的同时，也可以绘制开环Bode图。在“Control and Estimation Tools Manager”界面上选择“Graphical Tuning”，在Plot2的“Plot Type”下选择“Open-Loop Bode”，结果如图2所示。

4) 选择SISO Design for SISO Design Task界面的“Analysis-Responses to step command”，可在新界面LTI Viewer for SISO Design Task中得到原系统的单位阶跃响应曲线，如图3所示。由于分析闭环控制系统输出响应，故点击右键勾去“Systems-Closed Loop r to u(green)”。在LTI Viewer for SISO Design Task界面上分析阶跃响应的同时也可以分析闭环控制系统的Bode图，方法为在SISO Design for SISO Design Task界面中选择“Analysis-Closed-Loop Bode”，由于题目给出的性能指标为时域性能指标，故只需绘制单位阶跃响应曲线。

图2　基于Rltool的原系统根轨迹和开环Bode图

图3　原系统的单位阶跃响应曲线

5) 在图2中，当用鼠标拖动根轨迹上的红色方框时，即改变闭环极点位置时，开环Bode图会随之发生变化，同时图3中的单位阶跃响应曲线也会相应地随之发生变化。但无论根轨迹增益K*如何变化(可认为加入P控制器)，稳态误差始终存在且不为0；或由题目可知，原系统为0型系统，针对阶跃输入信号始终存在稳态误差。因此原系统不符合控制系统要求的稳态误差为0，故为了消除稳态误差，应加入PI控制器或PID控制器。

6)首先考虑PI控制器。PI控制器相当于在原系统的开环传递函数中加入一个数值为0的极点和一个零点。在Control and Estimation Tools Manager设计界面中选“Compensator Editor”，则可在“Compensator”中改变控制器增益(Kp)，在“Pole/Zero”中添加一个数值为0的极点和一个零点，如图4所示，则得到校正后系统的根轨迹如图5所示，当Kp=1时，其对应的单位阶跃响应曲线如图6所示。

图4　设置PI控制器的增益及零极点位置

图5　加入PI控制器后校正系统根轨迹和开环bode图

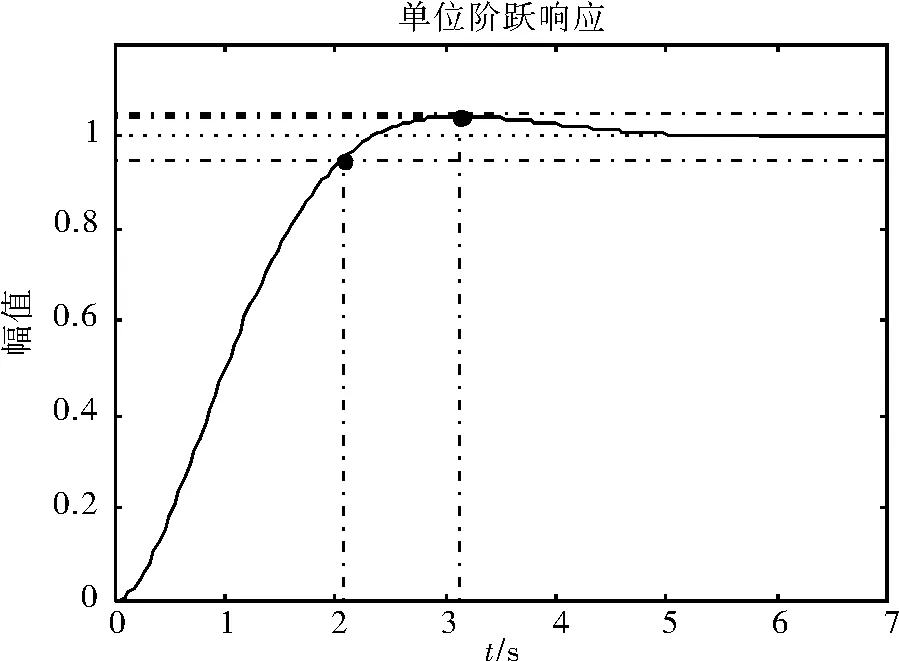
图6　加入PI控制器后校正系统单位阶跃响应曲线

当Gc(s)=Kp(s+1)/s时，只要0.5

7) 改变PI控制器零点位置，如令Gc(s)=Kp(0.8s+1)/s，只要0.74

由于例题中给定期望控制系统的时域性能指标，如给定频域性能指标，仍然可以采用此方法根据开环或闭环Bode图进行控制系统的设计。

通过上述步骤，按照经典控制理论设计的控制系统，其控制器不唯一，只需要改变控制器参数使之满足题目要求即可，这也与自动控制原理中校正装置的设计不唯一这一结论是一致的。

2.2模拟PID数字化

在计算机控制系统中，控制器为单片机或可编程逻辑控制器(programmable logic controller, PLC)等，它们只能处理数字信号，所以控制器应该选择数字PID控制规律。数字PID参数整定方法同样可以直接采用Rltool工具箱进行离散控制器的设计；也可以先采用2.1节的整定方法进行模拟PID参数整定，再采用双线性变换法将其离散化为数字控制器，即：

而采样周期可根据具体的被控对象系统进行选择[4]。

3　结束语

本文针对教学过程中学生面对实际系统不知如何采用自动控制原理的分析方法进行PID控制器参数整定问题，在已知表征被控对象的某一传递函数的基础上，利用Matlab自带的Rltool工具箱提出一种简单易行的PID参数整定的方法。实践表明此方法调整参数方便，容易掌握，并且有助于学生加深对采用时域、根轨迹和频域法分析和设计控制系统的理解。

[1]王素青, 姜维福.基于MATLAB/Simulink的PID参数整定[J].自动化技术与应用, 2009, 28(3)：24-25.

[2] 刘金琨.先进PID控制MATLAB仿真 [M].3版, 北京：电子工业出版社, 2011.

[3] 廖常初.PID参数最通俗的解释与参数整定方法[J].电气时代,2012(1)：90-94.

[4] 徐文尚.计算机控制系统 [M].2版, 北京：北京大学出版社, 2014.

[5]寸巧萍.自动控制系统实验教学中的仿真技术应用[J].实验科学与技术, 2007, 5(2)：57-53.

[6]刘金颂, 张庆阳, 苏晓峰, 等.Matlab软件在自动控制原理试验中的应用[J].实验技术与管理, 2014, 31(6)：138-140.

[7]闫明明, 杨平, 熊静琪.基于Matlab/Simulink辅助的《计算机控制技术》实验案例[J].实验科学与技术, 2014, 12(2)：53-55.

PID Parameters Tuning Methods Based on Matlab

ZHANG Jing, GAI Wendong, XU Wenshang, CHEN Zhiqiao

(College of Electrical Engineering and Automation, Shandong University of Science and Technology, Qingdao 266590, China)

On the basis of the known transfer function of the controlled object, aiming at the problem of the PID parameters tuning when teaching, a simple PID parameters tuning method is proposed in the paper using the Rltool built-in Matlab based on the basic knowledge of the Theory of Automatic Control.This method is easy to tune parameters and master in practice.Furthermore, it is useful for students to deeply comprehend the analysis and design the control system adopting time-domain, root locus and frequency-domain methods.

PID controller; parameters tuning; Matlab software; root locus

2015-04-07；修改日期: 2015-11-04

山东科技大学自动化学院名校工程建设项目(MX-JXGG-2)；山东省自然科学基金(ZR2014FQ008)；山东科技大学电气与自动化工程学院优秀教学团队建设计划资助项目(SKzdhjxtd152)；山东科技大学电气与自动化工程学院青年教师拔尖人才培育计划资助项目(SKzdhjxbj153)。

张婧(1982-)，女，博士，讲师，主要从事控制理论与控制工程方面的教学。

TP273

A

10.3969/j.issn.1672-4550.2016.04.010