应力空间下混凝土动态劈拉损伤演化方程及损伤界点的确定

吴　彬，胡伟华，唐克静

(1.湖北工业职业技术学院 建筑工程系,湖北 十堰 　442000；2.十堰市建筑设计研究院，湖北 十堰　442000; 3.三峡地区地质灾害与生态环境湖北省协同创新中心，湖北 宜昌　443002)



应力空间下混凝土动态劈拉损伤演化方程及损伤界点的确定

吴彬1，胡伟华2，3，唐克静1

(1.湖北工业职业技术学院 建筑工程系,湖北 十堰 442000；2.十堰市建筑设计研究院，湖北 十堰442000; 3.三峡地区地质灾害与生态环境湖北省协同创新中心，湖北 宜昌443002)

为研究混凝土动态劈拉特性，进行了不同应变速率下的混凝土动态劈拉试验，建立劈拉应力水平与声发射能量数的数学关系式，明确了混凝土劈拉损伤演化方程，提出了损伤界点的概念。基于医学ROC曲线确定最佳临界点理论,分析出了混凝土劈拉破坏损伤界点所对应的应力水平。研究结果表明：高应变速率下，损伤第1阶段声发射信号开始产生时的应力滞后，当应力水平超过一定数值后，损伤第2段的声发射现象与低应变速率时的相似；损伤界点随着应变速率的提高向应力水平较高处推移，其变化范围为[0.71,0.77]，且推移的规律服从线性分布，应力空间下混凝土劈拉损伤界点为0.75。

混凝土劈拉试验；声发射；损伤演化；ROC曲线；损伤界点

1　问题的提出

自从Doujill[1]将损伤力学应用到混凝土材料研究领域，国内外学者对混凝土材料的损伤研究一直没有间断过。关于混凝土损伤的研究，遵循了从单轴应力损伤到多轴应力损伤、从弹性损伤到弹塑性损伤、从静力损伤到动力损伤、从各向同性损伤到各向异性损伤的思路[2]。Dube等[3]从与应变速率无关的损伤模型中推导出与加载速率相关的损伤模型，并建立了考虑Perzyn黏塑性影响的损伤本构方程。Eibl等[4]在试验结果基础上，对混凝土损伤特性进行了分析，认为应变速率改变了混凝土在加载过程中的损伤路径。肖诗云等[5]构建以切线模量为参量的损伤变量,分析了混凝土动态损伤门槛值随应变率的变化规律和混凝土的动态损伤演化规律。李庆斌等[6]从混凝土动力损伤与静力损伤之间关系的角度，提出了考虑初始弹性模量变化的混凝土动力损伤本构模型的建立方法。李杰等[7]采用受拉损伤变量和受剪损伤变量建立了基于能量的弹塑性损伤本构模型，并进行了数值计算和试验验证。王春来等[8]根据Weibull统计分布理论和等效应变假定原理，建立了单轴受压状态下钢纤维混凝土损伤本构模型。

目前对于混凝土材料损伤的研究主要集中在损伤特性与损伤模型方面，但是对于混凝土损伤演化规律鲜有报道，而对于损伤阶段的划分和损伤界点的确定几乎无相关的研究成果。已有研究成果阐明混凝土单轴压缩损伤过程损伤存在着明显的3个阶段，即损伤萌芽阶段、损伤稳定发展阶段、损伤不稳定发展阶段[5]。损伤阶段所占整个损伤过程的比例对于研究混凝土损伤演化过程的规律具有重大意义。

因此，无论是混凝土单轴压缩还是劈拉试验，以何种方式来明确划分损伤阶段显得至关重要。鉴于此，进行了4种应变速率(10-5，10-4，10-3，10-2s-1)下混凝土动态劈拉试验，对劈拉过程中的混凝土声发射信号进行实时采集，通过确定劈拉应力水平与声发射能量数之间的关系，分析了混凝土劈拉损伤演化规律，并提出了损伤界点这一新概念，即损伤界点为前一损伤阶段的终点或者后一阶段的起点。

2　试验概况

2.1试验设备

试验采用的设备为10 MN微机控制电液伺服大型多功能动静力三轴仪。该设备可进行多种试件尺寸大小的混凝土动静力加载试验，具有多功能性。控制器最大采样频率为0.000 1 s，系统最大数据存储量为30万组样本，可实时自动采集数据及记录当前情况并反馈相关信息，实现存储、处理试验数据同步进行。声发射信号采集设备为SAEU2S系统。

2.2试件的制作与加工

2.2.1试件材料的选用

试验采用42.5普通硅酸盐水泥，搅拌混凝土所用的水为饮用自来水。

2.2.2配合比的确定及试件的养护与加工

试件采用ø150 mm×150 mm圆柱体试件。配合比根据《普通混凝土配合比设计规程》(JGJ55—2011)进行理论计算与试配，最终确定配合比为1∶0.56∶2.55∶3.83(水泥∶水∶粗骨料∶细骨料)。混凝土拌合料坍落度值在20～40 mm之间试件成型后48 h脱模，标准养护。

表2　不同应变速率下声发射能量水平统计

2.3试验步骤

(1)装样。确保试件的中心线和传力柱严格对中。

(2)声发射探头安装。通过耦合剂将声发射探头贴在试件平整的部位。

(3)声发射参数设置及检查。参数设置完毕后，进行声发射信号的检查，检查各个通道是否正常接收信号。针对本试验，声发射参数设置内容见表1。

表1　声发射仪器的参数设置

(4)变形计的安装与检查。

(5)试验加载。针对4种不同工况预先设好竖向加载的速率，在点击发送指令的同时开始采集声发射信号，加载到试件破坏为止。

3　基于声发射能量的劈拉损伤演化分析

3.1试验结果分析

试验得到的声发射撞击数与应力水平的对应关系如图1。其中σ0为峰值应力，Nmax为能量数最大值，N为能量数瞬时值。所谓应力水平是指应力与峰值应力的比值，即V=σ/σ0。

图1　不同应变速率下的应力水平与声发射能量水平的比较Fig.1　Relationship between stress level and energy number of AE under different strain rates

由图1可知，声发射数与混凝土应力水平V存在着一种更为直接的关系，现对混凝土劈拉试验的声发射能量水平n与相对应力水平的关系进行进一步分析。声发射能量水平n是指从初始状态到某一应力水平下声发射能量总数与应力水平为1时声发射能量总数之比，即n=N/Nmax。不同应变速率下的声发射能量水平的具体数值详见表2，声发射相对能量水平与相对应力水平的关系如图2所示。

图2　不同应变速率下能量水平与应力水平的关系Fig.2　Relationship between energy level and stress level under different strain rates

3.2试验结果拟合

从图2中曲线的走势可以明显地看出，应力水平<0.8时，声发射相对能量总数或损伤值基本维持在0，当应力水平>0.8时，声发射相对能量总数或者损伤值急剧上升。混凝土劈拉过程中混凝土损伤演化规律存在着明显的2阶段，即损伤发展阶段(损伤第1阶段)、损伤不稳定阶段(损伤第2阶段)。

(1)

(2)

根据式(1)和式(2)可得到声发射水平n与应力水平V之间的关系为

(3)

式中a，b，c为试验参数。

文献[11]阐明混凝土损伤可通过声发射能量数来表征并定义损伤变量为D=N/Nmax，结合本文给出的能量水平定义发现D=n，故损伤的表达式为

(4)

现利用式(4)对劈拉试验声发射损伤与相对应力水平进行拟合。拟合参数详见表3,拟合效果如图3所示。

表3　拟合参数值

图3　不同应变速率下声发射损伤与应力水平拟合关系Fig.3　Fitting relationship between AE damage and stress level under different strain rates

从拟合的效果来看，式(4)能较好地反映混凝土在劈拉过程中的损伤演化规律。因此，式(4)可用来进一步确定劈拉损伤界点。

4　基于ROC曲线的劈拉损伤界点确定

ROC (receiver operating characteristic)曲线是医学上将诊断试验结果划分为若干临界点,以每个临界点对应的灵敏度为纵坐标,特异度为横坐标,作图得到的曲线,是一种全面、准确评价诊断试验的有效工具[12]。ROC曲线的另一个作用是确定检测的最佳阈值[13]。ROC曲线法确定临界点多数情况下,选择曲线上尽量靠近左上方的点来确定临界点为最佳[14]。

本文将医学确定临界值的ROC曲线方法运用到损伤界点的确定过程中来，规定应力水平对应灵敏度，损伤对应特异度，即对劈拉损伤界点的确定转化为损伤演化曲线上的点到右下方点(1,0)的距离最短的点。

(5)

对式(5)求一阶导数为

(6)

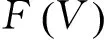
(7)

上述方程为超越方程，用目前的求根方法无法获得其精确解，只能对其进行数值分析运用改进的区间搜索法即二分法对其进行近似求解。

本文规定精度为ξ=0.001，由式(7)可知区间搜索的次数k=7,相关数据如表4所示,损伤界点应力水平与应变速率的变化关系及拟合曲线如图4所示。

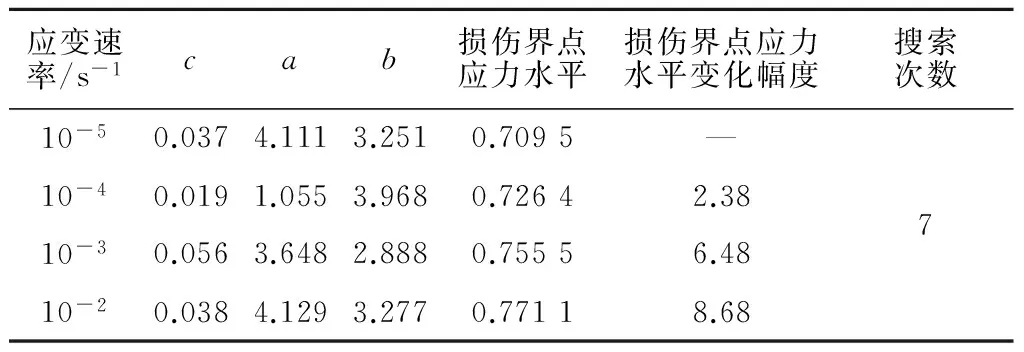
表4　区间搜索相关参数

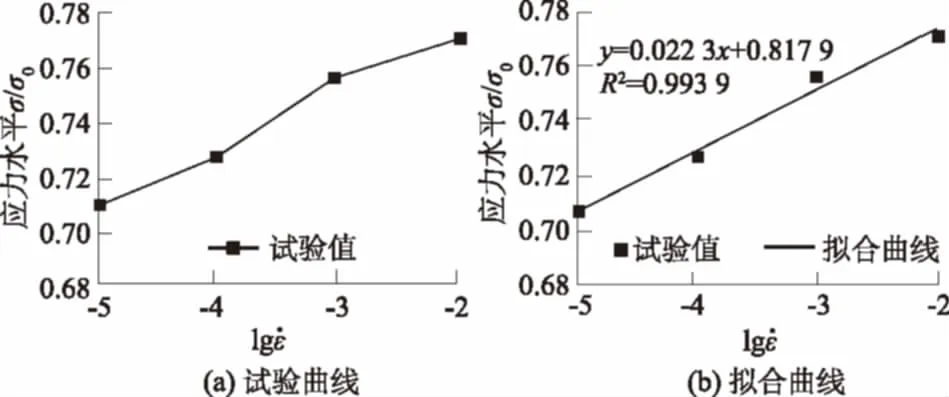
图4　损伤界点应力水平与应变速率的变化关系及拟合曲线Fig.4　Relationship between stress level at critical damage point and strain rate

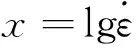
5　结　论

本文对劈拉过程混凝土材料所产生的声发射信号进行分析，建立了劈拉损伤值与应力水平数学关系，确定了混凝土劈拉损伤演化规律演化方程，提出了应力空间条件下混凝土劈拉损伤界点，得出的主要结论如下：

(1)在高应变速率下，声发射发展阶段明显滞后，当应力水平超过一定值后的声发射现象与低应变速率时的规律相似。

(2)试件劈拉破坏过程中，当相对应力水平<0.8时，损伤值在0附近波动，当应力水平>0.8时，损伤值急剧上升,说明损伤界点的应力水平在0.8附近波动。

(3)损伤界点随应变速率的变化范围为0.71～0.77，变化的幅度范围为2.38%～8.68%，应力空间条件下的劈拉损伤界点可取0.75。

[1]DOUGILL J W.On Stable Progressively Fracturing Solids[J].Journal of Applied Mathematics and Physics,1976,27(4):423-437.

[2]封伯昊,张立翔,李桂青.混凝土损伤研究综述[J].昆明理工大学学报(自然科学版)，2001,26 (3):21-30.

[3]DUBE J F,PIJAUDIER-CABOT G,BORDERIE C L.Rate Dependent Damage Model for Concrete in Dynamics[J].Journal of Engineering Mechanics,1996,122(10):939-947.

[4]EIBL J,SCHMIDT-HURTIENNE B.Strain-rate-sensitive Constitutive Law for Conpcrete[J].Journal for Engineering Mechanics,1999,125(12):1411-1420.

[5]肖诗云,张剑.不同应变率下混凝土受压损伤试验研究[J].土木工程学报,2010,43(3):40-45.

[6]李庆斌,邓宗才,张立翔.考虑初始弹模变化的混凝土动力损伤本构模型[J].清华大学学报(自然科学版),2003,43(8):1088-1091.

[7]李杰,吴建营.混凝土弹塑性损伤本构模型研究Ⅰ:基本公式[J].土木工程学报,2005,38(9):15-20.

[8]王春来,徐必根,李庶林,等.单轴受压状态下钢纤维混凝土损伤本构模型研究[J].岩土力学,2006,27(1):151-154.

[9]纪洪广，张天森，蔡美峰，等.混凝土材料损伤的声发射动态检测试验研究[J].岩石力学与工程学报,2000,19(2):165-68.

[10]MATSUYAMA K，ISHIBASHI A,OHTSO M.Rate Process Analysis of AE Activity in Core test of Deteriorated Concrete[C]∥ Japanese Society for Non-destructive Inspection.Proceedings of the 11th International Acoustic Emission Symposium,Fukuoka,Japan,October 26-29,1992:112-115.

[11]张明，李仲奎，杨强，等.准脆性材料声发射的损伤模型及统计分析[J].岩石力学与工程学报,2006,25(12)：2493-2501.

[12]ZWEIG M H，CAMPBELL G .Receiver-operating Characteristic (ROC)Plots:A Fundamental Evaluation Tool in Clinical Medicine [J].Clinical Chemistry,1993,39(4):561-567.

[13]王骏,吴虹桥,宋兆琪.受试者作业特征曲线(ROC)及其在影像学中的应用[J].放射学实践,2001,15 (3):201-202.

[14]陈卫中,倪宗瓒,潘晓平,等.用ROC曲线确定最佳临界点和可疑值范围[J].现代预防医学,2005,(7):729-731.

(编辑：姜小兰)

Determination of Critical Damage Point and Evolution Equation ofConcrete’s Dynamic Splitting Damage under Stress Space

WU Bin1,HU Wei-hua2,3,TANG Ke-jing1

(1.Department of Architecture,Hubei Industrial Polytechnic,Shiyan442000,China; 2.Shiyan Architectural Design Institute,Shiyan 442000,China; 3.Collaborative Innovation Center for Geo-hazards and Eco-Environment in Three Gorges Area of Hubei Province,Yichang443002,China)

In order to explore the features of concrete dynamic splitting,we carried out splitting test under different strain rates and established the relationship between stress level and AE(acoustic emission)energy number.Then,we put forward the concept of critical damage point and determined the evolution equation of dynamic splitting damage of concrete.On the basis of determining optimal critical point by using medical ROC(receiver-operating characteristic)curve,we gave the stress level of concrete at critical damage point in splitting test.Results showed that 1)under high strain rate,stress lags when emission signal occurs at the first stage of damage; 2)AE phenomena at the second stage were similar to those with low strain rate after stress level exceeded a given value; 3)with the increase of strain rate,the stress level at critical damage point increased,and its range was [0.71,0.77]; 4)there is a linear relationship between stress level at critical damage point and logarithmic function of strain rate,and the strain rate of concrete at critical damage point in splitting test under stress space was 0.75.

splitting test; acoustic emission; damage evolution; ROC curve; critical damage point

2015-06-02；

2015-08-12

吴彬(1989-)，女，湖北十堰人，硕士研究生，主要从事混凝土材料研究，(电话)18772846370 (电子信箱)1660621628@qq.com。

胡伟华(1988-)，男，湖南益阳人，硕士研究生，主要从事结构抗震设计和混凝土材料研究 ，(电话)18772803749 (电子信箱)464913988@qq.com。

10.11988/ckyyb.201504622016,33(08):125-129

TU502+.6

A

1001-5485(2016)08-0125-05