碎石尺寸对碎石土强度影响的大型直剪试验研究

吴　锐，邓清禄，付　敏，张腾飞，朱家畅

(1.中铁第四勘察设计院集团有限公司 地路处，武汉　430063；2.中国地质大学(武汉)工程学院，武汉　430074)



碎石尺寸对碎石土强度影响的大型直剪试验研究

吴锐1,2，邓清禄2，付敏2，张腾飞2，朱家畅2

(1.中铁第四勘察设计院集团有限公司 地路处，武汉430063；2.中国地质大学(武汉)工程学院，武汉430074)

以田师府—桓仁铁路大前石岭隧道边坡碎石土为研究对象，配置了3组含碎石尺寸不同的重塑碎石土样并采用大型直剪仪进行了剪切试验研究，探讨了碎石尺寸对碎石土抗剪强度的影响作用规律。在此基础上，利用现代非线性理论-分形理论，采用分形几何方法研究了该碎石土重塑样的粒度分布特征，得出了不同碎石尺寸下碎石土的分形维数，并探讨了碎石土的强度特征与粒度分形维数之间的关系。研究表明：在粗粒含量相同的情况下，碎石土的抗剪强度随着碎石尺寸的相对增大而增大；内摩擦角随着碎石尺寸的相对增大而增大；而黏聚力呈现相反的趋势，随着碎石尺寸的相对增大而降低；随着碎石尺寸的相对增大，分形维数增大，分形维数越大，其颗粒粒度分布越不均匀，反之分形维数越小，其颗粒粒度分布越均匀。碎石土抗剪强度和粒度分形维数有一定的相关性，黏聚力随着分形维数的增大而减小，而内摩擦角呈现相反的趋势，随着分形维数的增大而增大，黏聚力和内摩擦角均与粒度分形维数近似呈现抛物线函数关系。

碎石土；大型直剪；强度特性；碎石尺寸；分形理论

1　研究背景

随着现代工程的大规模建设及当代岩土力学界的发展，碎石土作为一种特殊的岩土体介质而越来越受到国内外学者的关注[1]。这种特殊的工程地质体在我国大规模的岩土工程建设中普遍存在，如边坡工程、深基坑工程及铁路和公路的路基、桥基等工程中，其物质组成主要以角砾、碎石、块石形成骨架，砂土、黏土等作为填充物[2]。碎石土与一般的土体不同，在松散堆积体滑坡中经常遇到这类土体，碎石土体中块石的粒径一般较大(几厘米到数米不等)。相对一般的岩土体来说，碎石土内部结构极为复杂，表现出很强的不均一性，内部“块石”强度较高而“土”又相对较软弱，“块石”和“土”所占的比例不同对其宏观力学性质、变形破坏特征影响极大。为区别于其他一般岩土体，Medley等[3]将其命名为block in matrix soil，简称Bimsoil；在国内油新华等[4]在对三峡库区蓄水边坡进行工程地质调查的基础上，正式提出了土石混合体的概念，即称之为“土石混合体”(soil-rock mixtures，S-RM)。

碎石土是复杂自然环境条件下的综合产物，这种特殊的工程地质体在我国乃至世界各地均有广泛分布，是一种不连续性的非线性体，成因及结构比较复杂，具有明显的不规则性、不确定性，并处于动态的不可逆演化之中，从而难以在基于传统的线性分析理论的基础上作出符合工程实际的定性或者定量的描述和分析。

自21世纪以来，随着分形理论的不断完善，土体的粒径分形特性研究逐渐成为岩土工程中研究的热门课题。国内外学者对土体粒度分形特性、粒度分布特征及其与土体强度间的相关性等方面进行了大量的探索研究。如N.Prosperini等[5]研究发现意大利Umbria地区土壤的粒度分布具有明显的分形特性；Medley[6]研究认为Francisca 地区分布的土石混合体内部粒度分布具有良好的自相似性；刘松玉等[7]研究得出我国黄土、红土和膨胀土这3类特殊土题的粒度分布具有明显的分形特征；Moore[8]对砂性土的分形特征研究得出砂土的粒度分形维数在1～2之间；Filgueira等[9]验证了阿根廷地区的5组黏粒(含量从8%到32%不等)的土样颗粒粒径分布分形模型；Casagli等[10]对意大利亚平宁北部的40多个堰塞体碎石土，采用现场整体量测、现场粗粒部分量测及细粒部分筛分和图像处理3种方法进行了粒度组成综合研究，获得的碎石土颗粒粒径分布分形相同；Tyler[11]、McBrathney[12]引入分形几何理论对颗粒和集合体分布的分形特征与规律进行了研究；谢和平[13]对土体内部的孔隙及颗粒分形进行了较为系统的研究并提出了一种孔隙分形维数的量测新方法；肖树芳[14]对黏性土的不均匀性与粒度分维之间的关系进行了研究；谢学斌等[15]研究得出某排土场散体岩石具有良好的粒度分布分形结构，其散体岩石的内摩擦角与分形维数为负指数关系；许勇等[16]对饱和软土颗粒分布分维值和孔隙分布分维值等微结构分形参数进行了研究；徐文杰等[17]通过现场筛分试验及数字图像处理技术对崩坡积碎石土的粒度组成进行了，研究得出碎石土内部的粒度组成分段分维特征比较明显，“粗粒相部分”与“细粒相部分”的粒度分界阈值为0.05～0.07Lc(Lc为特征工程尺度)；王宝军等[18]利用GIS技术对膨胀土类的微观结构图像进行分析，论证了膨胀土类的微观结构分形特性；舒志乐等[1]研究了碎石土的分形维数与其强度的关系；薛茹等[19]研究了软黏土在动力排水固结前后的微观结构分形特征，结果表明软黏土中的孔隙分布具有明显的分形特征，孔隙度分形维数可以用于地基加固程度的预测中；石修松等[20]研究了堆石料颗粒破碎的分形特性，得到了其围压、分形维数与颗粒破碎量之间的关系；谢静等[21]研究了交河故城崖体土的微观结构分形特征，建立了其分形维数与土的孔隙性及其抗压强度之间的关系。

近期动工兴建的田师府—桓仁铁路大前石岭隧道进口段开挖形成人工边坡，隧道进口自然坡度约22.5°，地势起伏，大部分为植被覆盖，少部分为裸露岩堆，岩堆石块主要为石英砂岩，石块直径0.3～1.2 m，呈块石土、角砾土及碎石土状，缝隙多充填黏性土，根据现场调查、钻探及物探结果，厚度为26.30～48.40 m，岩堆结构松散，空隙度大，植被发育地区充填细颗粒，局部具有软弱的黏结，下部地层为弱风化石英砂岩。边坡一旦失稳将严重威胁铁路运营及人民的生命财产安全。

分形理论的发展与完善为岩土体介质的微观研究创造了有利的条件。为此，本文以大前石岭隧道边坡碎石土为研究对象，基于分形理论，利用分形几何的方法研究了田桓铁路大前石岭隧道边坡碎石土大型直剪试验重塑样的粒度分布分形特征，得出不同碎石尺寸下碎石土的分形维数，并结合大型直剪试验结果探讨了碎石尺寸对碎石土抗剪强度影响作用规律并分析了抗剪强度参数与分形维数的相关性。

2　粒度分维数常见计算模型

常见的粒度分维数计算模型包括数量-粒径分形分布模型，质量-粒径分形分布模型，体积-粒径分形分布模型及颗粒表面分布分维。通过室内筛分试验获取土颗粒的质量分布情况比较容易，因此，国内外学者对土类的分形特性研究大多选择采用了质量-粒径分布分形模型，利用式(1)、式(2)进行计算，刘松玉等[7]、Moore等[8]研究了不同类别土体的分维数的变化，Filgueira等[9]认为分形维数随黏粒的含量增大而增大。

通常颗粒数量-粒径分布的通过试验难以测量，由于Turcotte[22]提出的数量-粒径分形模型存在颗粒数量测量上的困难，在假设颗粒密度相同的前提下，Tyler等人[11]推导出颗粒质量-粒径分布分形模型为

(1)

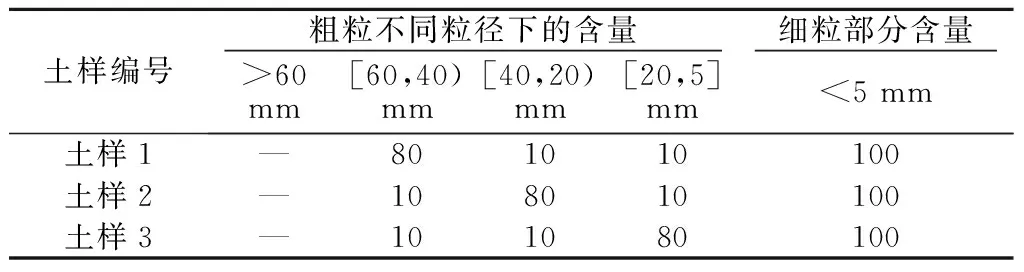
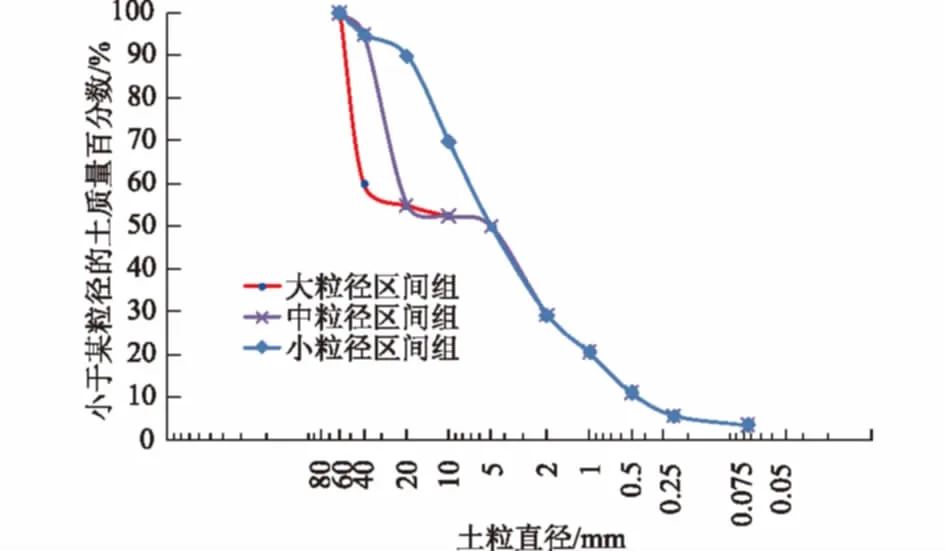
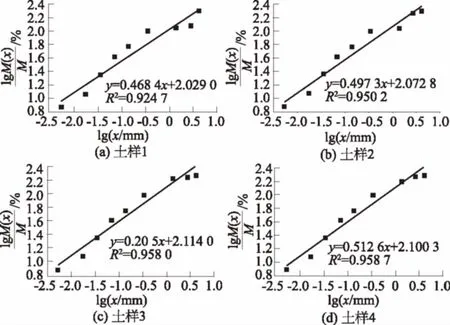
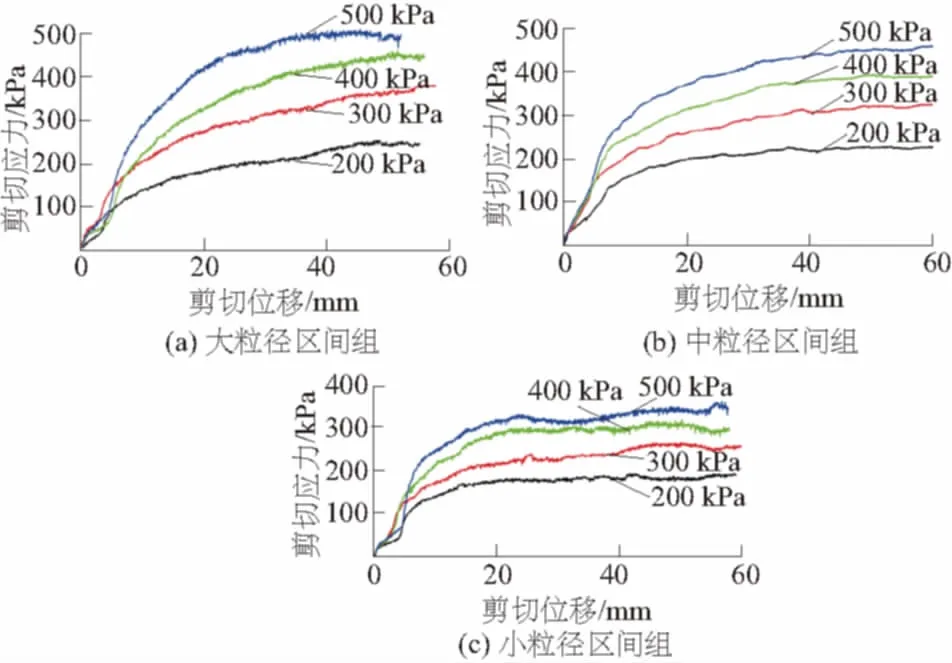
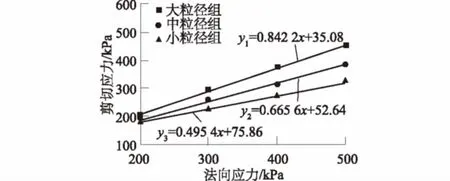
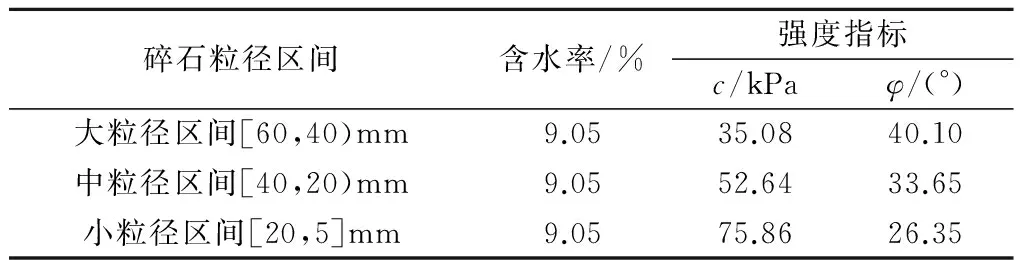
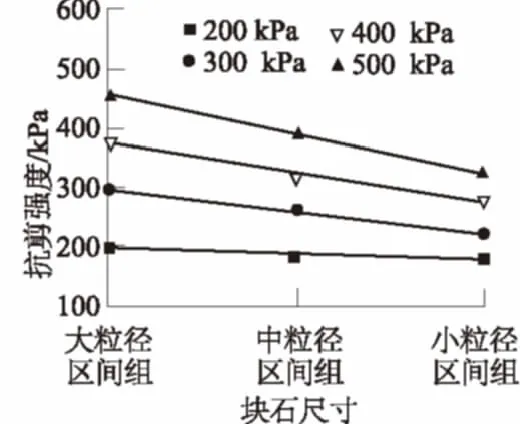
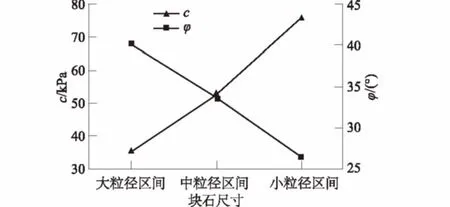
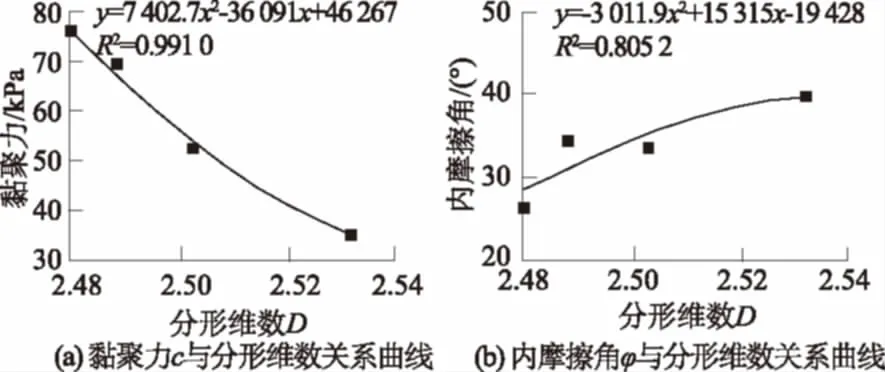
式中：M(r

一般对于碎石土这一特殊地质体选择采用以5 mm作为粗细料的分界粒径(粒径>5 mm为粗粒，粒径<5 mm为细粒)，其形成过程可用Menger海绵体来描述，因而，碎石土通常都具有多重分布分形的特性。考虑到碎石土的多重分形特性及粗、细料的粒径界限，建立其二重分形结构模型[23]。即

(2)

式中：M(x)为粒径小于x的颗粒质量(g)；M为颗粒总质量(g)；A(x)和B(x)为常数；x为颗粒粒径(mm)；D1为细粒粒度分维值；D2为粗粒粒度分维值。

3　试验方案及分维数的计算

3.1试验方案及土样的配置

将粗粒粒径尺寸分为3个区间等级，3个区间等级分别为60～40 mm，40～20 mm，20～5 mm，分别命名为土样1、土样2、土样3；配置3组不同粗粒粒径区间等级，粗粒含量均为50%的重塑碎石土样，其中细粒部分配比为天然级配、含水率为天然含水率9.05%。此外，另配置了一组粗粒含量也为50%，细粒部分级配为天然级配的重塑碎石土样，命名为土样4，作为对照试验土样，然后在4个不同的法向应力作用下采用室内大型直剪试验仪进行剪切，共计进行16个重塑土样的剪切试验。据此探讨碎石尺寸对土石混合体强度特性的影响，分析碎石土强度和分形维数之间的相关性。具体粒径级配配置含量见表1。

表1　不同碎石尺寸碎石土样配置结果

图1　不同碎石尺寸碎石土重塑样颗粒级配

3.2分维数的计算

考虑到颗粒粒径-颗粒数量难以获得，故通过筛分试验得到颗粒的质量分布后，选择采用颗粒质量-粒径分布分形模型，鉴于本文试验中重塑样的细粒部分含量相同，故直接利用式(1)、式(2)进行综合分形维数的计算，计算结果如表2所示。

表2　各重塑样粒度分形计算结果

根据大前石岭碎石土重塑样各粒径组质量的配置情况，采用Origin数据处理软件，作出其粒径(x)-筛下累积百分比([M(x)/M])在双对数坐标中的关系曲线并进行线型拟合，如图2，则3-D数值上就是拟合直线的斜率，进而可求得相应无标度区间的粒度综合分形维数D，最后得出4不同碎石尺寸下碎石土的综合分形维数分别为D1=2.531 6，D2=2.502 7，D3=2.479 5，D4=2.487 4。

图2　不同碎石尺寸下碎石土重塑样粒度分形曲线Fig.2　Fractal curves of remolded gravel soil samples of different stone sizes

从图2可知：在粗粒含量相同的情况下，随着碎石尺寸的相对增大，分形维数增大，拟合数据的离散性越大。分形维数越大，其颗粒粒度分布越不均匀；粒度分维数越小，其粒度分布越均匀，颗粒粒度分形维数能很好地反映碎石土颗粒组成和粒度分布规律。

4　试验结果整理与分析

试验采用中国地质大学(武汉)长江三峡地质灾害研究中心秭归试验基地配置的微机控制电液伺服1 000 kN大型直剪仪，试样最大尺寸为500 mm×500 mm×400 mm(长×宽×高)，大型直剪仪所允许的最大粒径为60 mm。为了尽量减小粗粒土的尺寸效应，本文中试验容许的粗粒粒径设置为最大值60 mm。3组不同碎石尺寸重塑试样分别在法向应力为200,300,400,500 kPa下进行剪切试验，试验过程中计算机数据采集系统自动进行数据采集，将试验数据导入Origin进行处理后绘制出其应力-应变曲线如图3所示。

图3　不同碎石尺寸重塑样应力-应变关系曲线Fig.3　Stress-strain curves of remolded soil samples of different stone sizes

试验采用的是固结快剪，从图3可以看出，3组不同碎石尺寸下的碎石土重塑土样在各级法向应力作用下剪切时均没有出现明显的峰值强度，在大粒径区间组及中粒径区间组时，应力-应变曲线呈现为应变硬化型，而小粒径区间组在高法向应力时，逐渐呈现出弱应变软化型。

3组不同碎石尺寸下的重塑土样应力-应变曲线均大体可分为3个阶段：① 弹性变形阶段，此阶段应力-应变曲线近似为直线，中粒径区间组试样的弹性阶段较为明显；② 屈服阶段，随着碎石相对尺寸的增大，剪应力达到峰值强度前的屈服阶段历时愈长；③ 应变硬化阶段，在同一法向应力下，随着碎石相对尺寸的增大，碎石土应变硬化程度明显升高。同种碎石含量下，在应变硬化阶段，低法向应力时，剪应力增长缓慢。随着法向应力的增加，剪应力迅速增长，应变硬化阶段曲线将较陡，其变形破坏机制在很大程度上不仅受到内部粗粒含量的影响，与碎石尺寸的大小也密切相关。

采用Origin数据处理软件作出其剪切应力-法向应力曲线如图4，并对4种不同法向应力下的剪切应力进行线型回归拟合分析，试验拟合结果见表3。

图4　不同碎石尺寸下剪切应力-法向应力关系曲线

碎石粒径区间含水率/%强度指标c/kPaφ/(°)大粒径区间[60,40)mm9.0535.0840.10中粒径区间[40,20)mm9.0552.6433.65小粒径区间[20,5]mm9.0575.8626.35

由图4可以看出：在粗粒含量相同时，抗剪强度随着碎石相对尺寸的增大而增大，抗剪强度增大的幅度也随着碎石相对尺寸的增大而增大；在同种法向应力下，抗剪强度随着碎石相对尺寸的增大而增大。造成这种试验结果的原因可能是，随着试样中碎石相对尺寸的增大，而细粒土部分含量又充足时，碎石土体能达到最大密实度，碎石与碎石之间及碎石与细颗粒之间都紧密接触，从而引起在剪切过程中颗粒之间产生较大的摩擦力。在剪切破坏过程中，大尺寸碎石在不断地发生移动、旋转，甚至翻越邻近碎石，发生剪胀现象使得克服这种剪胀变形作用的咬合力增大，从而抗剪强度增大。

图5　不同法向应力下抗剪强度-碎石尺寸关系曲线Fig.5　Relationship between shear strength and stone size in the presence of different normal stresses

由抗剪强度-碎石尺寸关系曲线图5可以看出抗剪强度随着碎石相对尺寸的增大而增大，随着法向应力从200 kPa增大到300 kPa时，抗剪强度升高的幅度增大，而后增加到400 kPa时，升高的幅度又渐缓，最后当法向应力增大为500 kPa时幅度又增大。在同种碎石相对尺寸下，抗剪强度随着法向应力的增大而增大。

为了研究碎石土抗剪强度参数与碎石尺寸之间的关系，强度指标随碎石相对尺寸变化曲线汇总如图6。

图6　强度指标随碎石尺寸变化曲线Fig.6　Variation of strength index with stone size

从图6中可以看出：内摩擦角φ随着碎石土内碎石相对尺寸的增大而增大，而黏聚力呈现相反的趋势，随着碎石相对尺寸的增大而降低。这是因为一般对于黏性土而言，其抗剪强度主要呈现在黏聚力c上，表现出“土”性；而对于碎石含量较大的碎石土，其抗剪强度则主要表现在内摩擦角φ上，表现出“石”性。在含石量相同的情况下，随着试样内碎石尺寸的相对增大，碎石与碎石之间的孔隙愈大，使得细粒部分慢慢逐渐不足以填充碎石之间形成的骨架，碎石土由“土”性渐渐转化为“石”性，碎石相对尺寸越大，“石”性所占优势越大。因此，随着碎石土内碎石相对尺寸的增大，内摩擦角增大而黏聚力降低。

5　抗剪强度参数与分维数的相关性

根据大型直接剪切试验结果，不同碎石下各组碎石土试样的强度参数指标见表3，为了更清楚地分析不同碎石尺寸下碎石土重塑样的抗剪强度指标黏聚力c及内摩擦角φ的变化规律，将试验数据导入Origin作出不同碎石尺寸下c-D及内φ-D的关系曲线如图7所示。

图7　黏聚力c及内摩擦角φ与分形维数关系曲线Fig.7　Variations of cohesion c and internal friction angle φ with fractal dimension

从图7可以看出：

碎石土黏聚力随着分形维数的增大而减小，与分形维数的关系可近似采用抛物线拟合，拟合具体函数为：C=7 402.7D2-36 091D+46 267，拟合系数R2=0.991 0，拟合情况极好。

碎石土内摩擦角随着分形维数的增大而增大，与分形维数的关系也可近似采用抛物线拟合，拟合具体函数为：φ=-3 011.9D2+15 315D-19 428，拟合系数R2=0.805 2，拟合情况一般，受试样数量的限制，难以建立其与碎石土分形维数的较为准确的关系曲线，在以后的试验中有待逐步完善补充。

6　结　论

(1)碎石土颗粒粒径分布线型关系明显，拟合系数均在0.92以上，分形特征比较明显，颗粒粒度分形维数能够很好地反映碎石土的颗粒组成和粒度分布规律，通常分形维数越大，其颗粒粒度分布越不均匀，粒度分形维数越小，其粒度分布越均匀。随着碎石土内碎石尺寸的相对增大，分形维数越大，拟合数据的离散性也越大。

(2)碎石土抗剪强度不仅仅受到其内部粗粒含量的影响，还与所含碎石的相对尺寸密切相关。随着碎石相对尺寸的增大，抗剪强度增大，抗剪强度增大的幅度也随着碎石相对尺寸的增大而增大。内摩擦角随着碎石土内碎石相对尺寸的增大而增大，而黏聚力呈现相反的趋势，随着碎石相对尺寸的增大而降低。

(3)不同碎石尺寸下的碎石土重塑土样剪切时的应力-应变曲线均大体可分为3个阶段，即弹性变形阶段、屈服阶段和应变硬化阶段，且均没有出现明显的峰值强度。在大粒径区间组及中粒径区间组时，应力-应变曲线呈现为应变硬化型，而小粒径区间组在高法向应力时，逐渐呈现出弱应变软化型。随着碎石相对尺寸的增大，剪应力达到峰值强度前的屈服阶段历时愈长。

(4)碎石土抗剪强度与粒度分形维数也有一定的相关性。黏聚力随着分形维数的增大而减小，而内摩擦角呈现相反的趋势，随着分形维数的增大而增大；黏聚力和内摩擦角均与粒度分形维数近似呈现抛物线函数关系。

[1]舒志乐,刘新荣,刘保县等.土石混合体粒度分形特性及其与含石量和强度的关系[J].中南大学学报(自然科学版),2010,41(3):1096-1101.

[2]王新刚,胡斌,刘强，等.碎石土大型直剪研究与边坡稳定性分析[J].长江科学院院报,2013,30(6):63-66.

[3]MEDLEY E.The Engineering Characaerization of Mélanges and Similar Block-in-matrix Rocks(Bimrocks)[D].Berkeley:University of California at Berkeley,1994.

[4]油新华,汤劲松.土石混合体野外水平推剪试验研究[J].岩石力学与工程学报，2002,21(10):1537-1540.

[5]PROSPERINI N,PERUGINI D.Particle Size Distributions of Some Soils from the Umbria Region:Fractal Analysis and Numerical Modelling[J].Geoderma,2008,145(3/4):185-195.

[6]MEDLEY E,LINDQUIST E S.The Engineering Significance of the Scale-independence of Some Franciscan Melanges in California,USA[C]∥Proceedings of the 35th US Rock Mechanics Symposium.Rotterdam:A.A.Balkema,1995:907-914.

[7]刘松玉,方磊,陈浩东.论我国特殊土粒度分布的分形结构[J].岩土工程学报,1993,15(1):23-29.

[8]MOORE C A,DONALDSON C F.Quantifying Soil Microstructure Using Fractals[J].Geotechnique,1995,1(45):105-116.

[9]FILGUEIRA R R,FOURNIER L L,CERISOLA C I,et al.Particle-size Distribution in Soils:A Critical Study of the Fractal Model Validation[J].Geoderma,2006,134(3/4):327-334.

[10]CASAGLI N,ERMINI L,ROSATI G.Determining Grain Size Distribution of the Material Composing Landslide Dams in the Northern Apennines:Sampling and Processing Methods[J].Engineering Geology,2003,69(1/2):83-97.

[11]TYLER S W,WHEATCRAFT S W.Fractal Scaling of Soil Particle-size Distribution Analysis and Limitations[J].Soil Science Society of America Journal,1992,56(2):362-369.

[12]MCBRATHNEY A B.Comments on Fractal Distribution of Soil Aggregate-size Distribution Calculated by Number and Mass[J].Soil Science Society of America Journal,1993,57:1393-1394.

[13]谢和平.分形几何及其在岩上力学中的应用[J].岩土工程学报,1992,14(1):14-24.

[14]肖树芳.泥化夹层的组构及强度蠕变特性[M].长春:吉林科学技术出版社,1991.

[15]谢学斌,潘长良.排土场散体岩石粒度分布与剪切强度的分形特征[J].岩土力学,2004,25(2):287-291.

[16]许勇,张季超,李伍平.饱和软土微结构分形特征的试验研究[J].岩土力学,2007,28(增刊):49-52.

[17]徐文杰,胡瑞林,岳仲崎.基于数字图像处理的土石混合体细观结构研究[J].辽宁工程技术大学学报:自然科学版,2008,27(1):51-53.

[18]王宝军,施斌,刘志彬,等.基于GIS的黏性土微观结构的分形研究[J].岩土工程学报,2004,26(2):244-247.

[19]薛茹,胡瑞林,毛灵涛.软土加固过程中微结构变化的分形研究[J].土木工程学报,2006,39(10):87-91.

[20]石修松,陈展林.堆石料颗粒破碎的分形特性[J].岩石力学与工程学报,2010,29 (2):3852-3857.

[21]谢静,谌文武,程佳,等.微结构分维与孔隙率及抗压强度的关系[J].兰州大学学报(自然科学版),2009,45(2):26-30.

[22]TURCOTTE D L.Fractals and Fragmentation[J].Journal of Geophysical Research B,1986,91(2):1921-1926

[23]陶高梁,张季如.表征孔隙及颗粒体积与尺度分布的两类岩土体分形模型[J].科学通报,2009,54(6):838-846.

(编辑：王慰)

Large Direct Shear Test on the Influence of Stone Sizeon the Strength of Gravel Soil

WU Rui1,2,DENG Qing-lu2,FU Min2,ZHANG Teng-fei2,ZHU Jia-chang2

(1.Department of Subgrade,Road and Bridge,China Railway Siyuan Survey and Design Group Co.,Wuhan 430063,China；2.Faculty of Engineering,China University of Geosciences,Wuhan430074,China)

The influence of stone size on the shear strength of gravel soil was investigated through large direct shear test on three groups of remolded gravel soil specimens of different stone sizes.The gravel soil in the slope of Daqianshiling Tunnel in the Tianshifu-Huanren railway was taken as research object.On this basis,the characteristics of grain size distribution of the gravel soil specimens were researched by using fractal theory.The fractal dimension of gravel soil with different stone sizes was obtained,and the relationship between shear strength parameters and fractal dimension was studied.Results indicate that when stone content is the same,shear strength and internal friction angle increase with stone size increasing; on the contrary,cohesion decreases along with the increase of stone size.With the increase of stone size,fractal dimension increases,and as fractal dimension gets bigger,the particle distribution is more uneven,and vice versa.There is a certain degree of correlation between shear strength parameters and fractal dimension.With the increase of fractal dimension,cohesion decreases whereas internal friction angle increases; cohesion and internal friction angle have approximately parabolic function relationship with particle fractal dimension.

gravel soil; large direct shear test; strength characteristics; stone size; fractal theory

2015-05-12；

2015-06-01

吴锐(1990- )，男，湖北孝感人，助理工程师，硕士，主要从事岩土稳定性评价与地灾防治及铁路勘察与设计等相关研究工作，(电话)15071462872(电子信箱)728411259@qq.com。

邓清禄(1962-)，男，福建上杭人，教授，博士后，主要从事输油气管道地质灾害防治方面的研究工作，(电话)13871165007(电子信箱)Dengqinglu@163.com。

10.11988/ckyyb.201503972016,33(08):80-85

P642

A

1001-5485(2016)08-0080-06