几何直观——数学教学的应然之道

江苏泰州市姜堰区东桥中心小学南校区（225500） 刘桂兰

几何直观
——数学教学的应然之道

江苏泰州市姜堰区东桥中心小学南校区（225500） 刘桂兰

教师要重视几何直观的教学，引导学生经历转直观、做直观、画直观、放直观、想直观等阶段，帮助学生不断积累运用几何直观解决问题的经验，逐步培养学生利用几何直观解决问题的能力。

几何直观动手操作转直观做直观放直观想直观画直观

由于几何直观凭借图形的直观性特点，将抽象的数学语言与直观的图形语言、抽象思维与形象思维结合起来，不仅能充分展现问题的本质，而且能够帮助学生打开思维的大门。所以，课堂教学中，教师应注重几何直观的教学，引导学生突破数学理解上的难点，使学生真正理解和掌握所学的知识。

一、开始阶段：前后沟通——转直观

传统数学领域之间的界限日趋消失，而几何直观在其中起着重要的联系作用。如“分数乘分数的算法”就是其中一个典型的例子，教材在学习整数乘分数时就已经注意引导学生借助几何直观来帮助理解。因此，教师在引导学生进行图形操作前，一定要让学生思考三个问题，即“分什么“”怎么分“”怎么取”。课堂教学中，教师可这样讲解：“整数乘分数是把一堆事物直接拿来分一分、取一取就可以了，而分数乘分数（如）分的是，先要分一分、取一取，得到后，再将分一分、取一取，才能得到的。”教师可以用直观图显示如下过程，使学生产生直观感受：因为分了又分，所以分母相乘；因为取了再取，所以分子相乘。这样教学，使学生真正理解了所学的知识。

二、新授阶段

1.动手操作——做直观

由于现代信息技术的广泛应用，有些数学课堂过渡依赖课件，一些需要动手操作的实验也用课件演示，导致学生的数学活动缺乏实践的体验。例如，教材中的“探索规律”专题活动，部分教师将其中的观察、操作、实验等各种数学活动省去，不注重学生探究的过程，只重视规律探究的结果。这样课堂上应有的生动活泼不见了，反而使学生失去了智慧的灵性。

2.图文变换——画直观

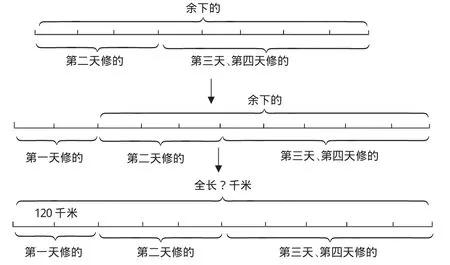
小学数学教材中特别注重数形结合思想的渗透，通过图形的直观性来阐明数之间的联系，将许多抽象的数学概念和数量关系形象化、简单化，实现代数问题与图形之间的互相转化、相互渗透。这样不仅能使解题简洁明快，还开拓了解题思路。如：“修路队用4天时间修完一段路。第一天修了120千米，第二天修了余下的37.5%，第三天、第四天修了全长的50%。这段路全长多少千米？”这道题中37.5%和50%的单位“1”不一样，画图时就要琢磨一下4天所修路程的长短关系，进而画出下图。这样从图中就能清楚地看出第二天修了全程的30%，可以用常规的方法求出全长为600千米，也可以直接得出120÷2×10=600（千米）。

3.运用技术——放直观

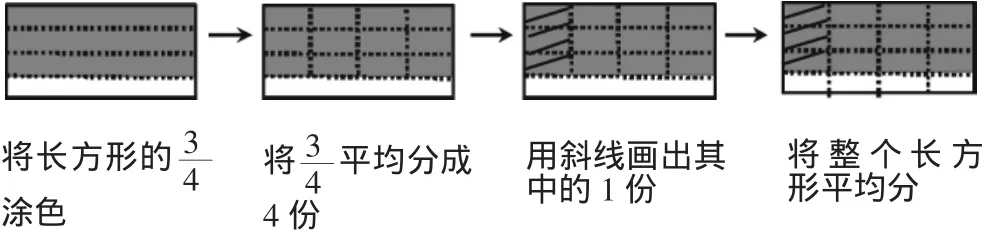
立体图形的学习对小学生来说难度不小，课堂教学中充分运用好多媒体，能使学生易于理解所学的知识。例如，教学“表面涂色的正方体”一课，目的是让学生探索切成的小正方体中隐含的规律。学生通过实际操作，发现把大正方体的每条棱平均分成的份数比较少时可以操作，份数渐渐多时比较困难。这时教师可出示直观图，为学生的直接观察做铺垫，从而提高了课堂教学的效果。

三、提升阶段：闭目思考——想直观

直观是手段，抽象是直观的发展，而直观的目的是为了更好地理解抽象的知识。随着学生年级的升高和抽象思维能力的增强，教师应逐渐减少学生对直观演示的依赖性，提高学生的抽象思维能力。例如，教学分数应用题时，可先让学生借助图形理清数量关系，然后逐步减少对图形的依赖性，直至最后完全不用画图也能解决问题。

总之，培养和发展学生的几何直观，需要依托具体的数学内容。因此，教师要重视几何直观的教学，帮助学生不断积累运用几何直观解决问题的经验，使不同的学生获得不同的发展。

［注：该文是江苏省教育科学“十二五”规划立项课题（编号D/2013/02/200）《运用现代信息技术，培养小学生直观能力研究》的研究成果。］

（特约编辑木清）

G623.5

A

1007-9068（2016）21-026