基于流量与占有率模型的交通事件检测器布设研究
邵长桥,李 敏
(北京工业大学交通工程北京市重点实验室,北京 100124)
基于流量与占有率模型的交通事件检测器布设研究
邵长桥,李 敏
(北京工业大学交通工程北京市重点实验室,北京 100124)
为了解决在不同的交通运行状态下事件检测器布设间距的问题,在理论推导的基础上,考虑交通运行状态与交通流模型的适用性,结合道路实测数据,得到分阶段的流量-占有率函数模型;应用标定的流量-占有率,结合交通波传播模型与交通事件检测原理,通过仿真的方法确定事件发生后道路占有率,分别确定道路处于高占有率和低占有率运行状态下,交通事件检测器的布设间距.检测器响应时间为1 min,在低占有率状态下检测器布设间距为1.0 km,在高占有率状态下间距宜为0.5 km.
交通流模型;交通事件;流量-占有率;检测器布设间距
通过布设检测器来快速、准确地检测突发事件对于减少延误和改善交通运行是一种行之有效的方法[1-2].为了合理地优化检测器布设间距,高建立等[1]运用单截面法,分别对轻交通量和重交通量状态下的检测器布设间距进行了研究,给出了检测器布设间距理论模型.Xing等[3]针对交通需求不确定性的情况,提出了检测器布设最优间距模型;Piya等[4]考虑了以起讫点(OD)估算为目标的双目标优化问题来确定检测器布设位置和间距;Liu[5]应用非线性整数规划模型研究了单向高速公路上检测器的布设间距;Bartin等[6]考虑了检测器布设间距对行程时间估计精度的影响,研究了高速公路检测器布设间距与行程时间估计误差的关系,并以此为基础,给出了检测器布设间距建议值;Kim等[7]、陈雨人等[8]和王彦杰等[9]分别基于遗传算法、最短路径搜索算法以及有向环图建立了交通检测器布设优化模型;王静[10]运用单截面、双截面事件检测方法,依据事件信号最大传播时间的允许值给出了检测器布设间距理论推荐值;方青[11]以VISSIM为平台,选择人工神经网络作为事件检测算法,研究了高速公路基本路段检测器布设间距.
在以往的研究中,通常将密度作为交通状态与服务水平划分的依据,但是密度的测量比较困难,而且精度较低.而占有率作为一个易于检测的指标,对于交通状态的判定具有一定的敏感性[12].因此,本文根据密度与占有率的关系,在传统的交通参数模型的基础上,推导出适用于不同交通状态的流量-占有率分段函数模型,并用其计算交通事件检测器的布设间距[13].
1 基于占有率的交通流模型
1.1密度与占有率的关系分析
时间占有率是指在单位观测时间内,车辆通过某一断面的累计时间占用的比率[14].根据时间占有率定义,其计算公式为
根据时间占有率的定义可以推导出流量、速度、密度和占有率之间的关系式
因此,密度与占有率之间的关系可以表示为
式中:occ为时间占有率,%;T为观测时间,s;ti为第i辆车通过观测断面的时间,s;为第j辆车通过观测断面的平均时间,s;n为观测时间内通过观测断面的车辆,辆;为第j辆车的平均车长,m;vj为第j辆车平均速度,km/h;k为观测路段上车流密度,辆/ km;g为交通组成修正因子,即
式中:l为车辆平均长度,m;d为检测器长度,m.
由式(2)~(7)给出的占有率与密度的关系可以发现,对给定的检测器,在交通组成相对稳定的情况下,时间占有率与密度存在线性关系[15].由于密度难以直接测量,实际应用中往往需要根据流量与速度观测数据进行换算,因此,应用实测占有率替代密度,可以避免转换带来的误差,相对而言更加精确[16].
1.2流量-占有率关系模型
研究人员发现,由于交通需求和车辆运行特性以及道路设施服务能力的相互作用,不同状态下交通流呈现出不同的运行特征[17],并提出了用不同的模型来刻画不同状态下的交通流.其中,Uderwood[18]与Greenberg[19]分别建立适用于低密度(低交通需求和占有率)和高密度(高交通需求和占有率)的速度-密度模型.安德伍德模型为
把式(3)代入式(5),得到基于安德伍德模型的速度-占有率模型
根据q=kv,进一步推导出安德伍德模型[18]对应的流量-占有率模型
当车流密度较大时,交通流运行速度和密度之间的关系可以由格林柏格模型[19]描述
应用同样的方法,得到相应的流量-占有率模型
因此,由式(7)(9)可得到分段的流量-占有率模型
式中:vf为自由流速度,km/h;q为流量,辆/h;occ为占有率,%;occ0为临界占有率,%;b1、b2、p1、p2为待标定的参数.
2 模型参数标定
本文应用数据为北京二环交通流检测数据.数据采集间隔为2 min.检测器的布设地点在二环东直门北入口处,分析的车道为外环的最外侧车道.
2.1交通流运行特性分析
图1、2分别给出了速度-占有率散点图以及流量-占有率散点图.由图可以发现,速度和流量在占有率为28%左右时,速度-占有率曲线和流量-占有率曲线出现了“空隙”,并且“空隙”前后,交通流状态出现了明显的变化,速度和交通流量显著下降.文献[16,20]经过细致分析发现,该“空隙”对应着交通流由非拥堵向拥堵状态转化的“相变”过程.因此,本研究以占有率28%作为交通流运行状态划分的分界点,将交通运行状态分为2种情况,即低占有率和高占有率运行状态.
2.2模型参数标定
基于实测的交通运行数据,运用SPSS分析软件对模型(13)的参数进行了标定.表1给出了参数标定结果.
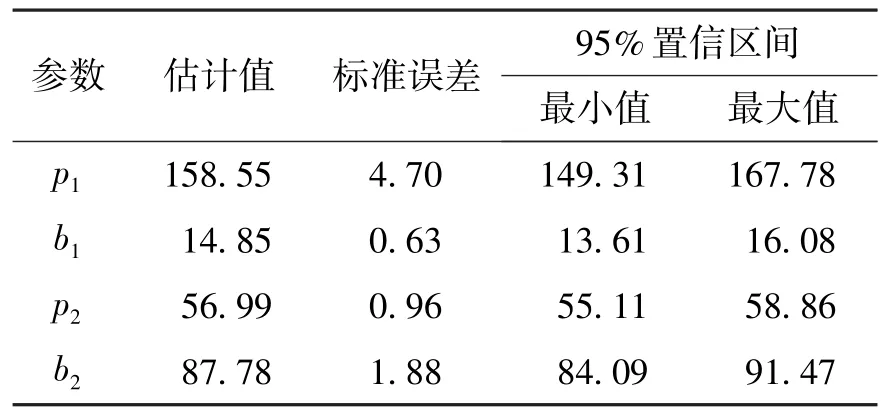
表1 模型参数估计结果Table 1 Model parameter estimates
因此,把表1中参数估计结果代入模型(13)得到标定后的分段流量-占有率模型
由模型(14)计算得到模型的拟合优度R2= 0.87,平均绝对百分比误差为7.51%.图3给出了标定模型对数据拟合情况.
3 基于流量-占有率模型的检测器布设间距
将上述推导的流量-占有率模型应用到高速公路事件检测器的布设间距研究中,运用交通波速传播原理,分别计算出低占有率和高占有率状态下检测器的布设距离.
3.1基于事件检测的检测器布设间距理论分析[1]当路段发生交通事件时,会导致该处交通运行速度下降,交通流阻塞(形成交通瓶颈).根据交通流理论可知:当路段发生阻塞时,阻塞地点会产生压缩波,并沿交通流方向向后传播,同时还产生扩展波,沿行车方向向下游传播,如图4、5所示.图4中C点为发生阻塞车辆的位置.C点上游则出现压缩波,依次传向检测器A(t1时刻),这时A点处交通流出现异常.同样道理,在瓶颈下游的车辆则以正常的速度向下游扩散.
假设压缩波断面为S,则断面S把该路段分为a、b两段(见图5).压缩波的波速用Vw1表示,可以按式(15)~(17)计算.
式中:k1、k2分别为路段a、b的车流密度,辆/km;q1、q2分别为路段a、b的交通流量,辆/h;occ1、occ2分别为路段a、b的占有率,%;occ0为临界占有率,%.
按照上述原理,a、b路段的检测器布设距离为
X1、X2的计算公式为
式中:t1-t0、t2-t0为交通参数变化传播到上下游的时间,s;vf为路段自由流速度,km/h.
目前,比较先进的交通事件检测算法采用的是双环形线圈数据[21],只要上游或者下游检测点检测到交通流参数变化,都将对交通事件做出反应,最不利的情况是发生的交通事件位于2个相邻检测点的中间位置,可要求检测器布设间距为
3.2仿真分析
应用实际数据进行仿真(见图6),结果表明:当仿真道路运行状态处于二级服务水平,流量为1 500 辆/h,速度为90 km/h,未发生事件时,车流会稳定行驶,速度保持在80 km/h以上,占有率稳定在13%左右;当发生交通事件时,稳定行驶的车流会发生阻塞,形成压缩波,造成车速急剧下降,车流密度和占有率迅速上升.其中,占有率的增量大于30%,而且会持续到车流开始疏散.所以,发生交通事件后,占有率的平均值约为45%.
由图7可见:当仿真道路运行状态处于四级服务水平,流量为1 800辆/h,设计速度为50 km/h,未发生事件时,车流会稳定行驶,占有率稳定在30%左右;当发生交通事件时,由于交通流量较大,会造成前方道路直接阻塞,事发点上游的速度变为0 km/h,而密度变成阻塞密度.
3.3检测器布设间距计算
当交通需求不大时,路段交通为低占有率状态,假设道路运行状态处于二级服务水平.路段发生交通事件引起堵塞时,产生的交通波传播至上游和下游的时间相等,且分别取1、2、3、5 min.由仿真分析得到,式(17)中发生交通事件前后的占有率分别取13%、45%,则计算得到检测器的布设间距如表2所示.

表2 低占有率状态下对应的检测器布设间距Table 2 Detector layout space under low occupancy
由表2计算结果可以发现,在低占有率情况下(对应低交通需求),假设交通事件传播至上、下游的时间分别为1、2、3、5 min,基于流量-占有率模型计算的检测器布设距离大致为1.0~3.5 km.如果要求事件检测的时间为1 min,则检测器布设的间距约为1.0 km.
当交通流占有率较高时,路段交通需求较大,交通运行压力持续走高,运行状况较差.假设道路运行状态处于四级服务水平,由交通事件产生的交通波传播至上游和下游的时间相等,且分别取1、2、3、5 min.式(17)中的占有率取30%.表3给出了基于流量-占有率计算的检测器布设间距.
因此,当交通需求较大,占有率较高时,检测器布设距离大致为0.5~3.0 km.当要求交通事件检测的时间为1 min,检测器布设的间距应为0.5 km.

表3 高占有率状态下对应的检测器布设间距Table 3 Detector layout space under high occupancy
4 结论
1)分阶段的流量-占有率模型可以用于拟合交通流运行状态.交通流状态可以分为低占有率状态和高占有率状态,不同交通状态用不同交通流模型刻画交通流特性更符合客观实际.
2)交通事件检测器布设间距与交通流运行状态、检测响应时间有关.在轻交通量和低占有率状态下,检测时间不大于1 min的情况下,检测器布设平均间距宜在1.0 km左右;在重交通量和高占有率交通状态下,检测器布设平均间距宜在0.5 km左右.
[1]高建立,薛飞.高速公路上检测器合理间距布设探讨[J].河南交通科技,1994,3(59):41-43. GAO J L,XUE F.Discussions on the reasonable layout spacing of the the highway detectors[J].Journal of Henan Transportation Science and Technology,1994,3(59):41-43.(in Chinese)
[2]张彬彬.高速公路交通事件检测算法及检测器布设方案研究[D].吉林:吉林大学,2002:15-18. ZHANG B B.Study on detection algorithm of traffic incidents and detectors distribution of freeway[D].Jilin: Jilin University,2002:15-18.(in Chinese)
[3]XING F,HANI S.Structural analysis of near-optimal sensor locations for a stochastic large-scale network[J]. Transportation Research Part C,2011,19(3):440-453.
[4]PIYA C,ANTHONY C.An objective traffic counting location for destination trip table estimation[J].Transport Metrica,2005,1(1):65-80.
[5]LIU H X.Optimal sensor locations for freeway bottleneck identification[J].Computer-aided Civil and Infrastructure Engineering,2009,24(8):535-550.
[6]BARTIN B,OZBAY K.Clustering-based methodology for determining the optimal roadway configuration of detectors for travel time estimation[J].Journal of the Transportation Research Board,2007,20(2):98-105.
[7]KIM J,PARK B.Determining the optimal sensor locations in freeway using the genetic algorithm-based optimization [J].Applications of the Artifical Intelligence,2011,2(2):17-19.
[8]陈雨人,郑仕文,童世鑫,等.区域高速公路网络交通事件传感器布设方法研究[J].公路交通科技,2010,3 (11):5-9. CHEN Y R,ZHENG S W,TONG S X,et al.Research on sensor placement method of regional highway network traffic incidents[J].Journal of the Highway Transportation Science and Technology,2010,3(11):5-9.(in Chinese)
[9]王彦杰,李文勇.基于图论的交通检测器新型布设方法[J].西部交通科技,2010(4):92-95. WANG Y J,LI W Y.New layout method of traffic detectors based on graph theory[J].Journal of Western Transportation Science and Technology,2010(4):92-95. (in Chinese)
[10]王静.高速公路交通检测器布设方案研究[D].西安:长安大学,2007:28-30. WANG J.Study on layout scheme of the highway traffic detectors[D].Xi’an:Chang’an University,2007:28-30.(in Chinese)
[11]方青.高速公路固定检测器布设方案分析[J].交通科技与经济,2010(6):6-8. FANG Q.Analysis on the layout scheme of the fixed detectors of the highway[J].Journal of Transportation Science and Technology and Economy,2010(6):6-8. (in Chinese)
[12]NIAAN N L.Evaluation of forced flows on freeways with single-loopdetectors[J].JournalofAdvanced Transportation,2000,34(34):269-296.
[13]刘政威.考虑交通事件检测的固定型交通检测器布设方法研究[D].南京:东南大学,2011:12-15. LIU Z W.Study on the layout method of fixed traffic detectorconsideringtrafficincidentdetection[D]. Nanjing:SoutheastUniversity,2011:12-15.(in Chinese)
[14]任福田,荣建.新编交通工程学导论[M].北京:中国建筑工业出版社,2011:27-28.
[15]WILLIAM H K.Optional speed detector density for the network with travel time information[J].Transportation Research Part A,2002,36:203-223.
[16]NIHAN N L.Freeway and ramp real time forecasting for improved real-time control and data analysis[J].Journal of Biophysical Ogtology,1961,9(3):724-725.
[17]TIAN Z,MICHAEL K.New perspectives on the twocapacityphenomenoninfreewayoperation[C]∥Transportation Research Board 84th Annual Meeting. Washington,D.C.:National Research Council,2005: 25-42.
[18]UDERWOODRT.Speed,volumeanddensity relationships:quality and theory of traffic flow[J]. Probability Theory,1990,2(2):141-148.
[19]GREENBERG H.An analysis of traffic flow[J]. Operations Research,1959,7:78-85.
[20]王尧,邵长桥,刘洋.城市快速路交通拥堵判定方法研究[J].交通信息与安全,2014(2):23-26. WANG Y,SHAO C Q,LIU Y.Research on the method of traffic congestion in urban expressways[J].Journal of Traffic Information and Security,2014(2):23-26.(in Chinese)
(责任编辑 梁 洁)
Study of Layout of Incident Detectors Based on Traffic Flow and Occupancy Models
SHAO Changqiao,LI Min
(Beijing Key Laboratory of Traffic Engineering,Beijing University of Technology,Beijing 100124,China)
In order to solve the problem of detectors layout space under different traffic operational states,a piecewise function model of flow-occupancy was presented theoretically and estimated by using the surveyed data,considering both traffic operational states and applicability of traffic flow models.Under the high and low occupancy states,combined the principle of traffic incident detection with traffic wave propagation model,the occupancy after the event was determined by the simulation method and the theoretical values of the detectors layout space were suggested on the basis of the flow-occupancy model. The detection response time of the event was supposed to be 1 min,the detectors distance was 1.0 km under the low occupancy,and the detector distance was 0.5 km under the high occupancy.
traffic flow model;traffic incident;flow-occupancy;space of detectors
U 491
A
0254-0037(2016)09-1392-06
10.11936/bjutxb2015110053
2015-11-18
国家“973”计划资助项目(2012CB723303)
邵长桥(1972—),男,副教授,主要从事交通流理论、道路通行能力、交通数据分析方面的研究,E-mail:shaocq@ bjut.edu.cn

