三电平逆变器多模式中点电压平衡策略

王凯凯，陈文博，万　衡（上海应用技术学院电气与电子工程学院，上海201418）

三电平逆变器多模式中点电压平衡策略

王凯凯，陈文博*，万衡
（上海应用技术学院电气与电子工程学院，上海201418）

逆变器一直是电气领域研究的热点问题，三电平逆变器的广泛应用得到了研究人员的大量关注，其中三电平逆变器存在的中点电压不平衡的问题限制了其使用，该问题也渐渐成为近期的研究热点。所提出的一种三电平逆变器多模式中点电压平衡策略和算法，较好地实现了中点电压平衡，通过仿真验证和实际工程应用，验证了该算法的可行性和可靠行。

三电平逆变器；中点电压平衡；混合式平衡；Bang-Bang控制

在大功率的场合，三电平逆变器与传统的两电平逆变器相比有诸多优点［1～3］，但是三电平逆变器存在中点电压不平衡的固有问题，许多文献［6～9］提出了多种改进方案，但仍然存在一系列缺陷，算法复杂是限制其工程应用的一个重要原因。针对三电平逆变器中点电压不平衡的问题，本文提出了一种三电平逆变器多模式中点电压平衡策略，使得控制周期内计算量大大降低，并且可以很好的稳定中点电压。

1　三电平逆变器中点电压平衡

三电平逆变器中点电压平衡，是指在三电平逆变器中，由于直流分压电容充放电不均衡造成的中点电压不平衡的问题。图1为三相三电平逆变器拓扑结构图。通过图1的三相电平值可以得到图2所示的三电平逆变器空间矢量图。

由图2根据矢量的长度，将其分为以下5类：大矢量，中矢量，正小矢量，负小矢量和零矢量。图3描述了不同的矢量对于中点电流的影响。在每一个电压分量情形下，流入中点的电流各不相同。

图1　三相三电平逆变器拓扑结构图

图2　三电平逆变器空间矢量图

图3　三电平逆变器空间矢量对中点电流的关系

在大矢量的作用下，如图3（a）和图3（b）所示。由于负载并未连接在中点，而是直接与Cl和C2构成同一回路，因此不存在流入或流出中点的电流，故这两种分量对电容电压没有影响。

在中矢量的作用下，如图3中的（c）所示。Cl和C2分别与三相负载构成独立的充放电回路，虽然两个回路的平均电流相等，但由于两个充放电的电流之间存在相位差，使Cl和C2的电压有不同步的波动，因此这种分量下电容电压会产生变化。

在小矢量的作用下，如图3（d）、图3（e）、图3（f）和图3（g）所示。交流负载仅仅连接在中点与正电平或负电平之间，即仅连在Cl和C2中的一个电容两端，这样就只有一个电容与负载构成充放电回路，当一个电容因充（放）电使电压上升（下降）时，另一个电容的电压会有相同程度的下降（上升）。因此，此分量对两个电容电压的平衡性影响较大大。

从图3中的分析可以看出，要确定中、小矢量对中点电压的影响，就要和中点电流的方向联系起来。各个分量流入中点的电流可总结如表1。

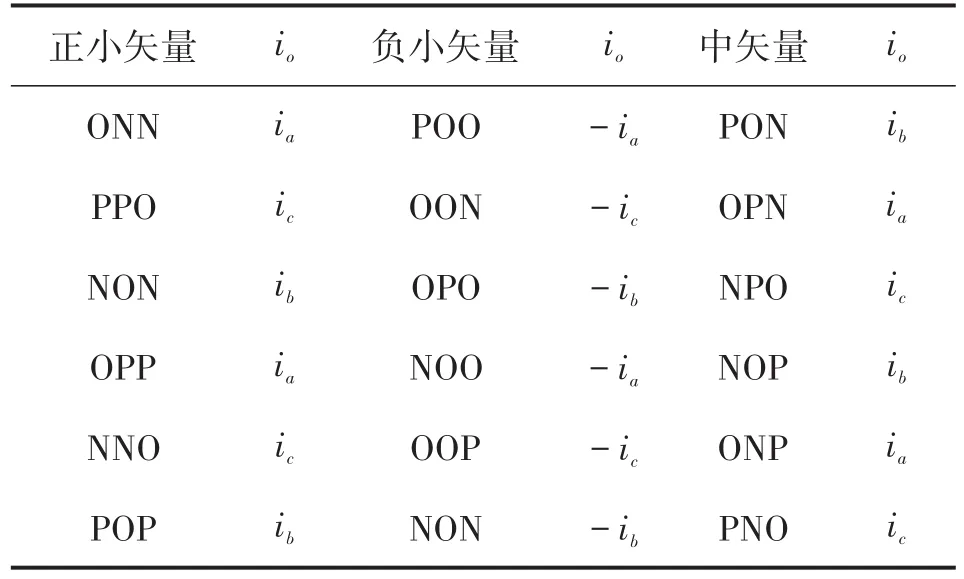
表1　中小矢量中点的电流

目前较为普遍的控制方式为引入时间控制因子，来分配每一个周期中小电压分量（矢量）的时间，使得每个周期中流入中点的电流为0。但是在实际控制中，该方法存在以下问题：目前所用的控制芯片大都采用DSP，其运算速度有限。用“时间控制因子”算法，需要消耗大量的计算资源，同时精确的浮点运算对于高频率控制来说相当困难，在每个周期中，DSP需要处理信号采集、转换、通信等一些列工作，完成该算法非常困难；在绝大多数情况，即使将影响中点电流的小分量（小矢量）全部替换，也无法使得本周期中平均中点电流为0。该情况下既浪费了大量的计算资源，又无法实现良好的控制效果。所以本文提出多模式中点平衡算法来解决中点电压平衡问题。

2　多模式中点电压平衡算法

本节将对多模式中点平衡算法进行详细介绍，以第I扇区为例，图4为三电平逆变器第I扇区电压矢量图，表2为I区Sn、S0、S1模式，

图4　三电平逆变器第I扇区电压矢量图

表2　I区Sn、S0、S1模式

表中落入第I扇区中各个小扇区的电压可由表2所示矢量表示，比如若电压矢量落入I-A区，可由OOO，POO，PPO，PPP四个矢量组合生成。表2中第1列与第4列所生成的电压一样，但是合成的矢量不同，结合表1可以看出，两种矢量对中点电流的影响正好相反。正常情况下，采用7段式PWM控制方案，表2中m取值0.5，定义此模式为Sn模式，该组合可定义为IA-Sn。由于OOO矢量对中点电流没有影响，所以m取值为1或0时，中点电压不变。我们定义m=0时，为S0模式；m=1时，为S1模式，其组合为IA-S0，IA-S1。

由表1可知，IA-Sn、A-S0和IA-S1中，流入中点的电流如式（1）：

若该式的电流符号不满足要求，则需要考虑改为另一种模式。

表3　IA-S2模式

表3为IA-S2模式，当IA-Sn、A-S0和IA-S1都无法满足中点电流要求时，可考虑采用此模式。此模式下流入中点的电流为式（2）：

式（2）与式（1）符号相反，因此，在IA扇区中，可以考虑此种变换模式。

再以I-C扇区为例：

在IC-S0模式时，电流为式（3）所示：

IC-S1模式时，电流为公式（4）所示：

在某些情况下，Sn，S0和S1可能都无法满足中点电流要求。这时就要使用S2模式。

表4是IA-S2模式，其流入中点电流为式（5）所示：

表5是IA-S3模式，流入中点电流为式（6）所示：

以上几种模式在PWM实现中，均满足每一个开关管在一个周期中切换一次的要求。

表4　IC-S2模式

表5　IC-S3模式

另外，对于B扇区和D扇区，只存在S0与S1模式。

若以上Sn，S0-S3模式均无法满足要求，并且重点电压值已经达到Vmmm或Vppp等级，此时需将三电平控制方式切换为两电平控制模式Sl，即每一项两个开关管当做两电平逆变器中一个开关管使用，此时对中点电压不造成影响，等待合适的周期出现来调整中点电压。具体的算法流程图下：

（1）检测中点电压，设Vp为电压高值，Vm为电压低值，Vpp为电压过高值，Vmm为电压过低值；

（2）判断中点电压所处区域（Vp，Vpp，Vm，Vmm）；

（3）当中点电压处于Vp与Vm之间时，本周期不变化矢量组合，采用Sn模式，判断结束；

（4）当中点电压＞Vp，本周期需确保流入中点电流为负（电流需要从中点流出）；当中点电压＜Vm，本周期需确保流入中点电流为正（电流需要流入中点）；

（5）若第4条成立，检测三相电流，读入电流值等待计算；

（6）判断所需生成电压所在大扇区；

（7）判断所需生成电压所在的小扇区；

（8）计算S0-S4组合下，流入中点的电流符号，计算采用定点计算，粗略计算出电流的正负和大小即可；

（9）以此刻中点电压＞Vp为例，此刻需要确保流入中点电流为负。按照第8步的计算，找出S0-S3中，电流为负且绝对值最大的组合Sx。若电压大于Vp但小于Vpp，且S0-S3中无一组合满足条件，则采用符号为正，或者符号为负但绝对值最小的模式Sx；若此时电压已经＞Vpp，则采取紧急策略，选择采用两电平控制方式Sl或直接并入平衡电阻，亦可同时采取两种方法进行控制；

（10）将Sx组合的PWM控制策略输出，本周期结束。

上面为多模式中点电压平衡算法的具体算法步骤，本算法的优点如下：

（1）在所有24个小扇区中，都有多种可替代的矢量组合，该组合在设计时提前编入程序，节省了多种组合在转换时所需的计算时间。这些组合变化较多，占用内存资源比传统方法多一些，因此对于DSP控制，可以看做用空间换时间的策略；

（2）此控制方式为Bang-Bang控制，控制规则简单，避免了每个周期都需要大量计算的情况；

（3）若想实现精确控制，可将Vpp与Vmm设置为中点电压值；

（4）当采并入中点平衡电阻也无法平衡电压时，可采用两电平控制策略，等待中点电压可控周期的出现，逐步将中点电压控制在安全范围之内。

3　算法仿真验证

上一小节提出了多模式中点电压平衡算法，并且给出了详细的算法步骤，为了验证算法的正确性和可行性，本节将对算法进行仿真验证，图5为仿真电路图，图6为扇区计算以及时间计算模块，图7为每一项PWM输出控制模块。

图5　仿真电路图

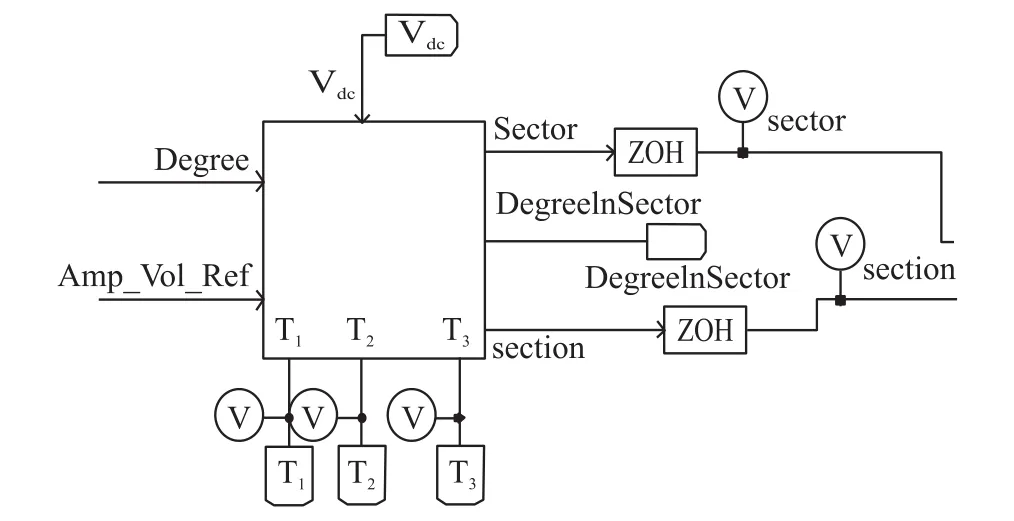
图6　扇区计算以及时间计算模块

图7　每项PWM输出控制模块

图7中，Vref代表输出参考电压值，Sector为大扇区，Section为小扇区，DegreeInSection为大扇区内的角度，T1-T3为计算出的时间。TA1-TC2为每项PWM的控制时间，ModeA1-ModeC2为控制每一项开关管开关的模式，取值为1或2，其中Mode1为开关管初始状态为0，整个周期的状态为0-1-0。Mode2为开关管初始状态为1，整个周期的状态为1-0-1。在上一小节的例子中，设置了Vp为251 V，Vm为249 V，仿真结果如图8～图10所示。

由仿真结果可知，本文所提出的多模式中点电压平衡算法是正确可行的，有效的控制了中点电压的平衡，相比传统的方法，该策略可以将电压较好的控制在目标范围内。

图8　与传统方法比较

图9　生成的A相电压

图10　C相电压斩波

4　总结

本文主要对三电平中点电压平衡的问题进行了详细的研究，首先分析了各矢量对中点电压平衡问题的影响，然后用实例的形式说明了多模式中点电压平衡算法并给出了详细的算法流程，最后通过仿真验证了所提的算法是正确有效的，且本算法已在实际生产中得到了应用，应用结果表明该算法稳定可靠，有很好的实际应用价值。

［1］ Pan Z，Peng FZ.Harmonics Optimization of the Voltage Balancing Control forMultilevel Converter/Inverter Systems［J］.IEEE Transactionson Power Electron，2006，21（1）：211-218.

［2］ 何湘宁，吴岩松，杨兵建，等.大功率三电平逆变器的开关模态转换状态的实时监测［J］.中国电机工程学报，2012，32 （30）：54-60.

［3］ Mekhilef S，Kadir M N.Voltage Control of Three-Stage Hybrid Multilevel Inverter Using Vector Transformation［J］.IEEE Transactions on Power Electronics，20l0，25（10）：2599-2606.

［4］ 伍文俊，钟彦儒，段博.三电平整流器弃用中矢量的对称三区电压矢量调制策略［J］.电工技术学报，2009，24（6）：69-76.

［5］ 陈鑫兵，何礼高.基于模糊控制的三电平逆变器中点电压平衡策略［J］.电工技术学报，2007，22（10）：103，108.

［6］ Oscar Alonso，Luis Marroyo，Pablo Sanchis，et a1.Analysis of Neutral Point Voltage Balancing Problem in Three-Level Neutral-Point-Clamped Inverterswith SVPWM Modulation［C］//Industrial Electronics Society，IEEE 2002 28th AnnualConference，2002，28 （2）：920-925.

［7］ 苑春明.三电平逆变器SVPWM关键技术研究［D］.合肥：合肥工业大学.2008.

［8］ 范必双，谭冠政，樊绍胜，等.一种新的基于混合空间矢量调制的三电平逆变器直流侧电容电压平衡研究［J］.中国电机工程学报，2012，32（27）：135-141.

［9］ Qiang Song，Wenhua Liu，Qingguang Yu，eta1.Aneutral-PointPotential Balancing Algorithm for Three-Level NPC Inverters Using Analytically Injected Zero-Sequence Voltage［C］//The Eighteenth Annual IEEE Applied Power Electronics Conference and Exposition，Miami，USA，2003：228-233.

王凯凯（1989-），男，汉族，江苏邳州人，硕士研究生，主要研究方向为电气智能控制与决策，wkaven@163.com；

陈文博（1986-），男，汉族，辽宁大连人，讲师，博士研究生，主要研究方向为电气控制与仿真，46742892@qq.com。

A Multi-Mode Neutral Point Voltage Balance Control Strategy of Three-Level Inverters

WANG Kaikai，CHEN Wenbo*，WAN Heng
（College of electronic&Electrical Engineering，Shanghai Institute of Technology，Shanghai 201418，China）

Inverter has always been a hot issue in the field of electrical research，the three level inverter iswidely used to geta lotofattention of the researchers，themidpointvoltage imbalance problem of three-level inverters limiting its use，this problem is becoming a research focus in the recent.Amultimodalmidpoint voltage balancing strategy and algorithm of three-level inverterswas proposed，itmaked themidpoint voltage balance.The algorithm was verified feasible and reliable by simulation and practicalengineering applications.

three-level inverter；neutral-pointvoltage balance；hybrid balance；Bang-Bang control

TM 464

A

1005-9490（2016）04-1005-05

2015-08-06修改日期：2015-09-26

EEACC:836010.3969/j.issn.1005-9490.2016.04.047