Hadoop下基于贝叶斯网络的气象数据挖掘研究

王　昊，师　卫，李　欢（太原理工大学信息工程学院，太原030024）

Hadoop下基于贝叶斯网络的气象数据挖掘研究

王昊，师卫*，李欢
（太原理工大学信息工程学院，太原030024）

为了提高传统朴素贝叶斯分类器对气象数据挖掘的精度，拥有更高的处理海量数据的效率，提出了一种Hadoop平台下基于离散贝叶斯网络的数据挖掘改进算法。算法不要求属性之间相互独立，且充分结合Hadoop平台适应处理大数据的优点，利用海量数据选取预测因子来训练贝叶斯网络分类器模型，以达到预测温度的目的。实验结果表明，算法不但预测精度明显高于目前短期气候预测中采用的朴素贝叶斯算法，而且极大地提高了运算效率。

数据挖掘；贝叶斯网络；Hadoop；MapReduce；气象预测

自古以来气象预报在防灾减灾和国民经济建设中都发挥着巨大作用，随着社会经济的发展和人民生活水平的提高，如何更加准确高效的进行天气预测也越来越重要［1］。

传统基于朴素贝叶斯分类器［2］的气象预测算法在处理大规模数据时缺点越来越突出，主要表现为：一是没有充分考虑到气象属性的特点，仍以属性之间互不相关为基本出发点；二是随着气象预报要求的不断提高，气象数据计算规模急剧膨胀，其处理数据的效率已不能适应现代天气预测的要求。

针对上述不足，本文提出Hadoop［3］下基于贝叶斯网络的气象预测算法。该算法以贝叶斯网络［4］为理论依据，在Hadoop平台下，利用MapReduce［5］对贝叶斯网络结构学习中的预处理、模型训练和精度评估3个过程进行分布式并行处理，充分利用了海量的气象数据中蕴藏的大量有价值的信息。

1　贝叶斯网络

1.1朴素贝叶斯分类器和贝叶斯网络分类器

朴素贝叶斯分类器（Native Bayes）［6］是基于贝叶斯公式的一类简单概率分类器，它以各个属性间的条件独立性假设为前提，假定特征向量的各分量间相对于决策变量是相对独立的，也就是说各分量独立地作用于决策变量，因此构造过程简单，具有错误率小、稳定、健壮性强等特点。在气象数据量小的时代，这种条件独立假设还能保持比较高的准确性，但是在海量气象数据面前，这种假设的缺点变得越来越明显。

与朴素贝叶斯所不同，贝叶斯网络是一种概率网络，是基于概率推理的图形化网络，贝叶斯公式是这个概率网络的基础。它采用图形化的网路结构直观地表达变量的联合概率分布及其条件独立性，一个贝叶斯网络是一个有向无环图，由代表变量结点及连接这些结点的有向边组成。

一个完整的贝叶斯网络是由一个二元组B=（BS，BP），BS是贝叶斯网络结构，包括网络结构中的节点集合A，每一节点表示特定域中一个特征属性，还包括有直接关系的节点之间的有向边E，BP是每一节点都附有与该变量相联系的条件概率分布函数（CPT），如果变量是离散的，则它表现为给定其父节点状态时该节点取不同值的条件概率表（CPT），表示它们之间的概率依赖关系，当节点X没有父节点时，节点X的CPT中只有X的先验概率P（X），当节点X有k个父节点｛Y1，…，Yk｝时，节点X的CPT中是条件概率P（X|Y1，…，Yk）。可见，贝叶斯网是一种表示数据变量之间潜在关系的定性定量的方法，它使用这种图形结构制定了一组条件独立的声明和用于刻画概率依赖强度的条件概率的数字值。

1.2贝叶斯网络学习

贝叶斯网络具有牢固的数学基础，Pearl在其［1988］的专著［7］中奠定了贝叶斯网络的了基础理论。其中给出并证明了如下定理：

对给定的概率分布P（x1，…，xn），存在P的贝叶斯网络G，使，其中πxi是Xi的父结点集∏xi的配置。

贝叶斯网络学习一般包含两个内容，贝叶斯参数学习和贝叶斯结构学习，而贝叶斯网络学习的核心是对贝叶斯网络结构的学习。现在最流行的贝叶斯网络结构学习方法可分为两类，一类是基于搜索评分的学习方法，此方法过程简单规范，易于操作，但由于搜索空间大，一般只适用于变量少或在一定范围内的结构学习；还有一类是基于约束测试的学习方法，此方法过程比较复杂，但在一些假设下学习效率较高，而且在耗时方面，它往往要更快一些。现有的约束测试方法中，冗余边检测是在确定边的方向之前进行，这样无法准确地确定切割集，这就导致大量的高维条件概率计算，这样经常不能定向所有的边，这些都降低了学习效率和准确性［8］。

本文在此基础上提出了基于预测能力的贝叶斯网络学习方法。

1.3基于预测能力的贝叶斯网络学习

因为预测能力就是预测正确率，预测能力相同是条件独立性的充分必要条件［9］，这样预测能力便把变量之间弧的存在性与方向有机的结合在一起。此结构学习算法首先依次计算两个变量之间的预测能力，再根据条件预测能力确定弧的存在性及方向。

设有离散随机变量X1，X2，…，Xn，x1，x2，…，xn为变量的值；D是变量X1，X2，…，Xn产生的大小为N的随机数据集。

将F（Xi→Xi）定义为变量Xi的自预测能力，F^（Xi→Xi）记作F（Xi→Xi）的估计值；

将F（Xm1，…，Xmt→Xi）定义为变量 Xm1，…，Xmt对变量 Xi的预测能力，F^（Xm1，…，Xmt→Xi）记作F（Xm1，…，Xmt→Xi）的估计值。

第1步确定贝叶斯网络的初始结构

Xj→Xi；

Xi→Xj

第2步对初始结构进行调整

如果P（X|Y1，…，Yk）＞ρz，则添加弧Xj→Xi；

则删除Xi→Xj之间的弧；

定向为Xj→Xi；

第3步进行环路检验［11］

在经过第二步调整过的结构图中，我们要把没有父结点或没有子结点的结点和与他们相连的弧删除，在剩下的子图中依照刚刚的做法把这些结点和弧都删除，这样一直做下去，若始终没有出现一个每个结点都既有父结点又有子结点的子图，则说明结构图不存在环路。否则，存在环路。

2　本文算法实现

针对温度气象数据集特征，基于MapReduce改进贝叶斯网络算法的过程包括：数据预处理、模型训练和精度评估三大过程。其流程图如图1所示。

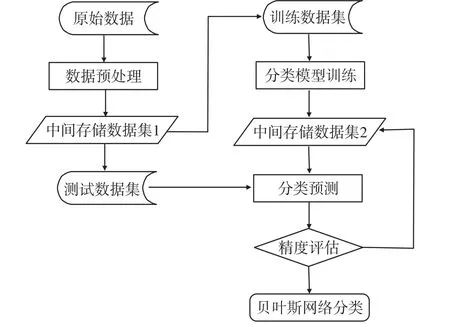
图1　算法流程图

2.1数据预处理

（1）数据清洗

气象数据质量的好坏直接影响着气象领域中数据挖掘的准确度。实验中采集到中国地面气候资料日值数据集中，存在缺省漏测和格式不一致的数据值，这严重影响到数据挖掘算法的执行效率，甚至有可能导致挖掘结果的偏差，故需要对数据集进行清洗。首先，基于MapReduce编程模型，统计含有缺失值的数据条数，结果显示日值数据集中含有缺失值的数据条数占总条数不到1%，因而直接采用把不完整的数据全部剔除出数据集；其次，基于MapReduce编程模型，对数据格式不一致的数据进行格式转换。最终使得数据集中的每一条数据都是格式一致的和完整可靠的。

（2）预测因子选择

基于MapReduce编程模型完成对温度和其他气象要素之间的相关性分析，选取合适的预测因子。对于任意两个气象要素X和Y，其相关系数的计算公式为：

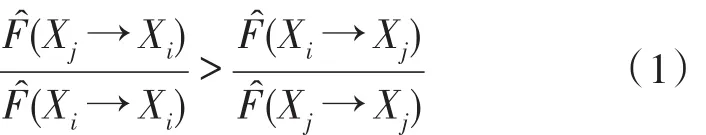
γXY取值在-1到1之间。当γXY=0时，称X与Y不相关；当|γXY|=1时，称X与Y完全相关，此时，X与Y之间具有线性函数关系；当|γXY|＜1时，X的变动引起Y的部分变动，γXY的绝对值越大，X的变动引起Y的变动就越大，一般情况下当|γXY|＞0.8时为高度相关，当0.5＜|γXY|＜0.8时为显著相关，当0.3＜|γXY|＜0.5时为低度相关，当|γXY|＜0.3时为不相关。

（3）数据离散化和整理

根据气温在一年中的分布情况，把气温按照温度的高低分为寒冷（-15℃以下），凉爽（-15℃～0℃），温和（0℃～15.9℃），暖和（15.9℃～25℃），炎热（25℃以上）5个级别。

数据预处理分为两个任务，一个是离散化预测因子，另一个是输出整理数据与温度分级标识。这两个任务是独立的，因此将这两个过程作为并行的MapReduce任务完成，定义Step1负责预测因子的区间离散化，定义Step2负责输出数据整理与温度分级标识。

①Step 1预测因子在数据集中以数字值的形式描述，因此需要对预测因子进行离散化操作。首先对预测因子和预测目标做标识，如下表所示：

离散过程中，我们采用PKI算法［12］，其一般采取离散区间大小等于离散区间数量的方法，但是在数据量巨大且分布不均匀的情况下，离散区间大小过大，会使得有些区间内没有值。针对气象数据大而不均的特点，我们令k=，以达到扩大区间的目的。

基于MapReduce编程模型完成统计预测因子的最大值和最小值，因此各个预测因子的离散化区间宽度w表达式如下：

②Step 2输出数据需要进行整理，定义当前日期为t，则前一日为t-1，整理后每一行数据为（t-2，t-1，t）的各个预测因子和明日的气温等级。Hadoop框架中的MapReduce的shuffle过程会将相同的key值放在一起，可以将t-2，t-1，t的各个预测因子所生成的key值设置为待连接的每一行，然后MapReduce框架会自行将其连接起来。

2.2模型训练

一般情况下，为了提高数据挖掘的准确度，将数据预处理中的J2整理的数据集分为两部分：80%训练集和20%测试集，训练集用于训练贝叶斯网络模型，测试集用于测试贝叶斯网络分类模型的精度。模型训练过程中，分为两大任务，一是统计各个温度级别频率和各个预测因子频率，另一是根据统计的频率计算各个预测因子之间以及预测因子与预测目标之间的预测能力，后一次的过程依赖于前一次的频率统计结果。

根据计算出的预测能力，运用第1节提出的算法，经过确定初始贝叶斯结构、调整初始贝叶斯结构和环路检验3个步骤，最终确定出贝叶斯网络的结构。

2.3精度评估

精度评估MapReduce过程中，将测试集分割成多个小块，对每一小块中各行数据通过分类模型进行预测，将预测结果与测试集中的温度真实数据进行比较，记录其正确与否的情况。最后用MapReduce统计预测情况，计算出正确率和预测率，公式如下：

正确率=正确分类数/实际分类数预测率=正确分类数/真实分类数在精度评估过程中，通过式（3）

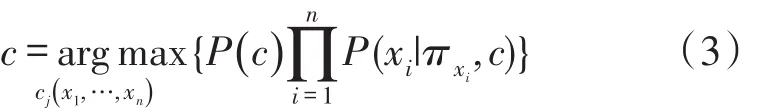
预测分类时，由于数据量大且分布不均，导致大量的条件概率相乘后，引起浮点数结果下溢的情况，因此对上式两边用求对数做处理，则c可表示为式（4）

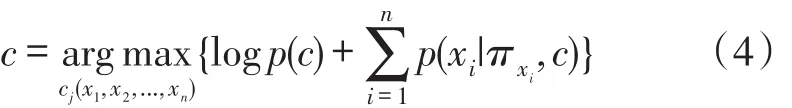
精度评估结果不理想时，需对模型重新训练，直到结果可以接受为止。

3　实验分析

3.1实验环境和数据

本文实验环境基于Hadoop云平台，采用完全分布式模式搭建于9台普通PC机上，其中一台为NameNode，其余八台作为DataNode。电脑的配置如下：3.4 GHz双核CPU、4 G内存、150 G磁盘、Linux CentOS 6.0操作系统、Hadoop 1.0.2版本。

研究数据来自中国的气象数据共享服务体系从1951年到2014年的环境数据，包括降水量、平均气温、平均气压、平均风速、平均相对湿度、日照时数、最大风速、最大风速的方向等其他因素。我们试验采取的数据是太原市从1951年到2014年底的全部数据。

3.2实验结果与分析

（1）相关性分析

首先通过对数据的清洗，把原来不完整、格式不正确的数据全部剔除出我们的数据库。然后对各类各类预测因子进行标识，并计算它们与气温之间的相关系数。计算结果如表1所示。

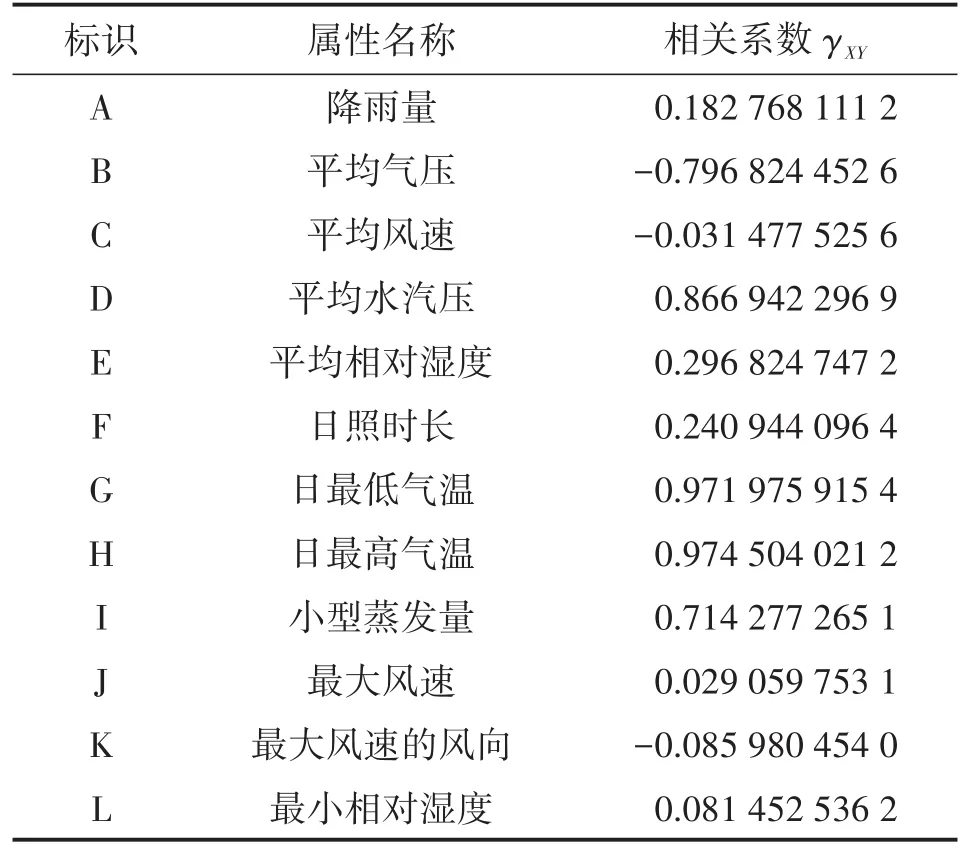
表1　各个气象要素与平均气温之间的相关系数

我们在试验中选取|γXY|＞0.3的气象要素作为预测因子，他们分别是平均气压B、平均水汽压D、日最低气温G、日最高气温H和小型蒸发量I，平均气温是我们的目标因子，我们用字母R作为它的标识。

（2）模型训练

取 ρc=ρz=ρj=1.1，根据计算出的变量之间的预测能力，得到初始的贝叶斯网络结构图，如图2所示。

调整贝叶斯网络结构，经过调整后的贝叶斯网络结构如图3所示。

图3　调整后的贝叶斯网络结构图

（3）精度评估

本实验的正确率和预测率如表2所示，其中R0代表寒冷，R1代表凉爽，R2代表温和，R3代表暖和，R4代表炎热。

表2　正确率和预测率

图4和图5分别展示了本算法和短期预测的朴素贝叶斯分类方法在正确率和预测率方面的对比，通过图形可以看出，不管是在正确率方面还是在预测率方面，本文算法都有较大的优势。

图4　正确率对比图

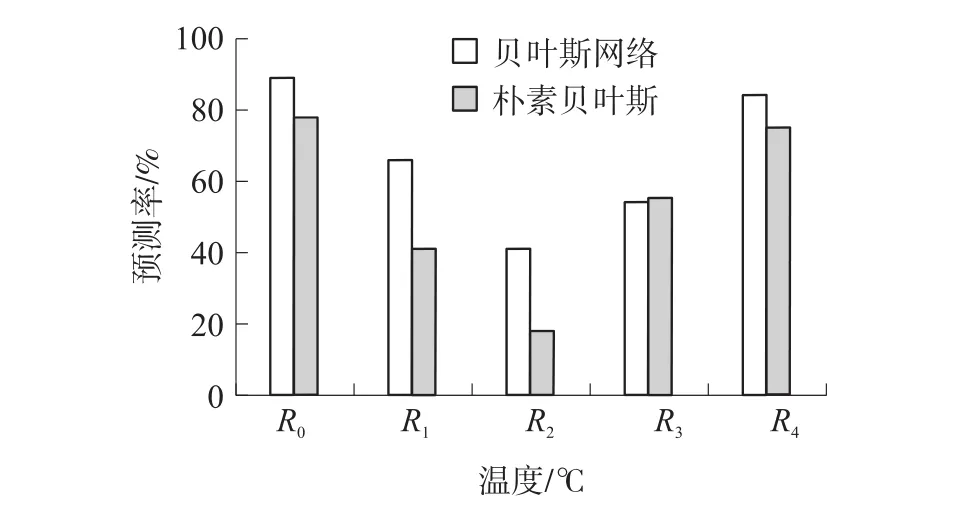
图5　预测率对比图

（4）效率评估

为了验证本文方案在海量气象数据情况下的运行效率，如图5，我们采用加速比对集群执行时间与单机时间进行对比。加速比公式定义为：

加速比=单机执行时间/集群执行时间

如图6所示，在数据量较大的情况下，本文方案的加速比接近于线性加速比。随着节点数的增多，对海量数据训练的加速优势也就越明显。

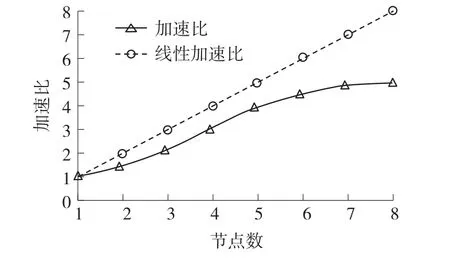
图6　加速比曲线

4　结语

本文对Hadoop下基于贝叶斯网络的气象数据挖掘进行了研究，给出了一种基于预测能力的离散贝叶斯网络结构学习和Hadoop相结合处理数据的新方法，该方法具有以下特点：（1）可以充分利用大数据时代下的海量数据，有效避免信息丢失及假依赖的出现（2）运算效率及准确率高于常规预测方法（3）不要求预测因子相互独立等，对预测因子要求不高（4）能够处理不完全、不精确或不确定训练数据集。在数据量不断飞涨的今天，此算法提供了在海量数据中挖掘有用的信息的新思路，其在电子商务、移动互联网、反恐等诸多领域的应用值得进一步研究。

［1］ 樊改娥，张顺利.浅谈气象预报的作用［J］.科技情报开发与经济，2008，18（16）：217-218.

［2］ 张晨阳，刘利民，马志强.云计算下基于贝叶斯分类的气象数据挖掘研究［D］.内蒙古：内蒙古工业大学，2014.

［3］ 李斌，张建平，刘学军.基于Hadoop的不确定异常时间序列检测［J］.传感技术学报，2015，28（7）：1066-1072.

［4］ 史志富，郭曜华.机载光电系统目标威胁估计的模糊贝叶斯网络方法［J］.传感技术学报，2011，24（11）：1584-1589.

［5］ Kadirvel SELVI，Fortes JAB.Towards Self-Caring MapReduce：A Study of Performance Penalties Under Faults［J］.Concurrency and Computation-Practice&Experience，2015，27（9）：2310-2328.

［6］ 赵力.基于贝叶斯压缩感知的说话人识别方法［J］.电子器件，2015，38（5）：1135-1137.

［7］ Peal J.Fusion ProPagation and Structuring in Belief Network［J］. Artificial Intelligence，1986，29：241-288

［8］ 马明，刘浩然.贝叶斯网络算法研究及应用［D］.秦皇岛：燕山大学，2014.

［9］ 张剑飞，王辉，王双成.基于预测能力的贝叶斯网络分类器学习［J］.计算机应用研究，2007，24（8）：50-52.

［10］Lam W，Bacchus F.Learning Bayesian Belief Network：An Approach Based on the MDL Principle［J］.Computational Intelligence，1994，10：269-293.

［11］李硕豪，张军.贝叶斯网络结构学习综述［J］.计算机应用研究，2015（3）：641-646.

［12］Yang Y，Webb G I.Weighted Proportional k-Interval Discretization for Naive Bayes Classifiers［C］//The 7th Pacific-Asia Conference on Knowledge Discovery and Data Mining（PAKDD），2009：501-512.

王昊（1989-），男，汉族，河北省保定人，太原理工大学信息工程学院，硕士研究生在读，主要研究方向为大数据挖掘，wanghao_tyut@163.com；

师卫（1956-），男，汉族，山西省朔州人，太原理工大学信息工程学院，副教授，主要研究方向为嵌入式系统研究、大数据挖掘，shi_w@163.com。

The Research of MeteorologicalData Mining Using Bayesian Network Based on Hadoop

WANG Hao，SHI Wei*，LI Huan
（Taiyuan Uniυersity of Technology Institute of Information Engineering，Taiyuan 030024，China）

In order to improve the precision of themeteorological datamining using raditionalnaive bayesian classifier，and own a higher efficiency ofhandling the huge amountsof data，this paper proposes an improved algorithm of discrete Bayesian network to predict the temperature.This algorithm can eliminate theweakness of naive bayesian method on the premise thatattributes are independentof each other，and combine the characteristics of the Hadoop platform processing large data.Usingmassivemeteorological data，it selects predictors and trains the Bayesian network classificationmodelon Hadoop platform.The experiments show that the improved algorithm isnotonly the accuracy is significantly higher than the short-term climate prediction using Naive Bayesian analysis，regression analysisand clusteranalysismethod，butalso improves the efficiency of the algorithm greatly.

datamining；bayesian network；hadoop；mapreduce；weather prognosis

TP301.6

A

1005-9490（2016）04-0841-06

2015-09-13修改日期：2015-11-19

EEACC:614010.3969/j.issn.1005-9490.2016.04.018