M orlet小波变换结合M LP神经网络的齿轮箱故障检测方法

合尼古力·吾买尔，林　玲（1.南京航空航天大学机电工程学院，南京210016；2.新疆交通职业技术学院运输管理学院，乌鲁木齐831401；3.伊犁师范学院电子与信息工程学院，新疆伊宁835000；4.南京大学计算机科学与技术系，南京210046）

M orlet小波变换结合M LP神经网络的齿轮箱故障检测方法

合尼古力·吾买尔1，2*，林玲3，4
（1.南京航空航天大学机电工程学院，南京210016；2.新疆交通职业技术学院运输管理学院，乌鲁木齐831401；3.伊犁师范学院电子与信息工程学院，新疆伊宁835000；4.南京大学计算机科学与技术系，南京210046）

针对变速齿轮箱中的故障检测问题，提出了一种结合Morlet小波变换和多层感知器（MLP）神经网络的齿轮故障检测方法。首先，利用角域技术将时域中齿轮故障的非平稳振动信号转化为角域中的平稳信号。然后，利用进行Morlet小波变换并从小波系数中提取统计特征。同时根据最大能量与香农熵比来确定连续小波变换（CWT）的最优尺度，以此来缩减特征量，并将小波系数的能量和香农熵作为两个新特征添加到特征向量。最后，利用MLP神经网络对输入特征进行分类，从而检测故障。实验结果表明，该方法故障检测准确率高，且计算速度快。

齿轮箱；故障检测；Morlet小波变换；多层感知器；神经网络；香农熵

齿轮箱已成为旋转机械的核心元件之一，轴承和齿轮缺陷是齿轮箱中存在的常见故障，目前，许多研究都是针对平稳过程中的旋转机械故障诊断［1］，只有少量的研究针对启动或停止过程中的故障。然而，在齿轮设备的启动或停止过程中，所有的激励量在幅值和频率上都会改变，并包含与其状态相关的丰富信息，可用来诊断设备启动时的齿轮裂纹缺陷等故障［2］。

连续小波变换CWT（ContinuousWavelet Transform）能够有效地对非平稳振动信号进行分析，从而检测故障。然而，CWT具有大量的冗余数据，使特征提取变得复杂，这就需要进行特性缩减［3］。本文基于香农熵与能量比例，来选择最优小波尺度，减少特征向量。人工神经网络（ANN）能够利用输入特征进行训练，并对特征分类，其广泛应用于机器状态诊断。本文选用前馈多层感知器MLP（Forward Multilayer Perceptron）神经网络对齿轮箱进行故障分类。本文方法能够准确检测多种齿轮故障，且网络训练时间短。

1　提出的故障检测方法

本文引入了连续小波变换（CWT）和神经网络来对齿轮箱启动时的故障进行检测。利用Morlet小波从原始振动信号的小波系数中提取统计特性用于分类，根据香农熵与能量的比值来确定CWT的最优尺度，减少特性量。最后，采用一个前馈多层感知器（MLP）神经网络（ANN）对特征数据进行分类。本文为提高ANN的分类准确性，添加能源和香农熵因子作为两个新特性。本文方法流程图如图1所示。

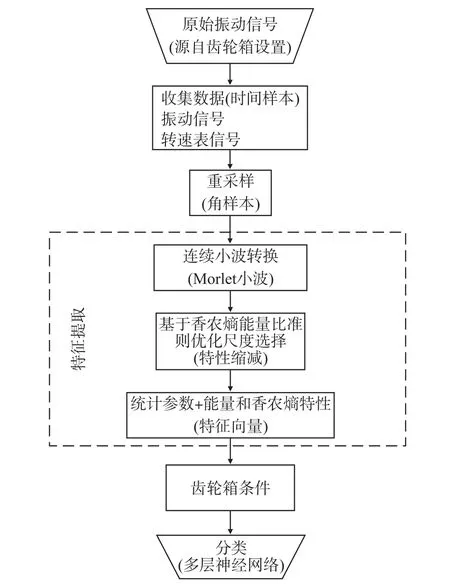
图1　故障检测系统流程图

1.1角域分析

齿轮箱轴的等角度位移数字采样称为角采样。角采样需要在来自常数时间采样信号的常角增量下完成振动信号采样，因此它与轴转速有关，则角域分析能容易地从振动信号中识别振动元件［4］。

为了描述轴角度θ（）t和确定重采样次数，可以假设轴以恒定角加速度旋转。因此，得到一个合适的二次方程：

通过提供发生在已知轴角增量Δϕ的3个连续键相到达时间（t1，t2和t3），则未知系数b0，b1和b2可以通过下式获得：

将这些条件带入方程（1），以矩阵形式给出

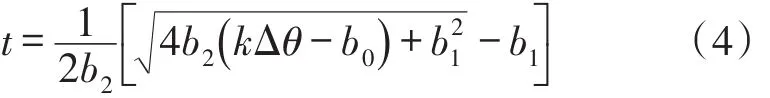
式中，k为插值系数，由下式得到：

式中，θ为轴角量，Δθ为重新取样样本之间的角间距。

当计算重采样次数时，利用采样数据之间的插值来计算相应的信号振幅。在角域中，实际采样率和监督窗口的时间周期随着转动轴转速的改变而改变。一个旋转期间内，事件总是在相同的相对位置发生，与齿轮箱的转速无关，这是角域的主要优点［5］。

对于变速机械监控中的非平稳噪声，单独的角域分析并不能提供一个有效可靠的基础，这时需要加入小波变换［6］。小波分析可以在时间和频率域提供局部特性和多尺度特性，这使得小波分析可以区分振动信号中的突变组件。

1.2连续小波分析（CWT）

小波变换具有可以同时检测稳定和瞬时信号的能力。

信号x（t）的连续小波变换定义如下［7］：

其中，

其称为母小波ψ（）t的子小波，在此定义中，其必须是实数，并满足∫［ψt］d t=0。在方程（7）中，a和b是实数参数，分别表示尺度和平移量。

Morlet小波可以同时抽取被检测信号的幅值和相位信息［8］。本文选用Morlet小波作为故障检测中的常用小波。Morlet小波表达如下：

式中，ω1为无因次频率。Morlet小波的函数是一个双边指数正弦信号，如图2所示［9］。

图2　M orlet小波图形

提取特征过程中，首次采用角域分析，将时间域上的振动信号转换成带常数角增量的角域信号，然后，采用连续小波变换（CWT）获取转换后信号的小波系数，提取小波系数的统计参数，构成特征向量。

1.3人工神经网络（ANN）

本文采用前馈多层感知器（MLP）神经网络对CWT中提取的特征进行分类。图3描述了一个多层神经网络，包含从输入信号的输入层，处理数据的隐藏层和输出识别结果的输出层［10］。

图3　三层神经网络结构

式中，x为输入向量，V和W分别为隐层和输出层的权重矩阵。为隐层激活函数（通常是一个c形或s形曲线），b为阈值，为边界神经网络近似误差。在误差反向传播训练过程中，将前馈阶段信号模式x提交到网络进而生成层响应y。在训练模式中，输出层误差，即传播给网络输入层，其中yd为期望的输出。利用最陡坡降法对权重进行相应的调整［11］。

根据如下公式所描述的更新规则，改变输出层和隐藏层权重，对输出误差进行离散化。

式中，η1和η2为设计者选择的学习率，=（1 2） ETE， E=yd-y为输出误差。考虑到输出层的激活函数是线性的，通过一些代数操作，可以对更新规则进行简化［12-13］：

式中，σd为隐层的激活函数σ（）.的导数。

2　实验及分析

2.1实验装置

本文采用的齿轮箱测试装置结构图和实际实验装置分别如图4（a）和4（b）所示。

图4　实验测试

实验装置中，驱动和被驱动齿轮分别有15和28个齿，传动比为28/15。本文考虑了两种齿轮缺陷：缺口和磨损。实验中准备了4个齿轮：正常齿轮，有缺口齿轮，磨损10%齿轮和磨损5%齿轮，如图4（c）所示。缺口情况中，从齿轮的齿廓到节面，沿着线性斜面切掉50%的区域。10%磨损情况中，在三个顺向轮齿的表面和侧面上，磨去0.5mm厚度（齿轮厚度的10%）。5%磨损情况中，在3个顺向轮齿的表面和侧面上，磨去0.3mm厚度（齿轮厚度的5%）。

在变速箱上安装一个加速度计，以10 kHz采样率采集振动信号。启动交流电动机，运转到的稳定速度（约为35 Hz，即2 100 rot/m），此过程中，加速度的频率在0～5 kHz的范围内。将采集的信号送入A/D转换器，然后将数据加载到MATLAB。MATLAB软件中，对振动信号重取样，将时间域上的非平稳信号转换成角域上的平稳信号，然后从采样数据中对测试齿轮箱产生的振动信号进行恒定角采样，再后利用连续小波变换（CWT）获取信号的小波系数，构成特征向量。

2.2最优尺度和特征选择

图5显示电机启动过程中，由正常齿轮、有缺口齿轮、磨损10%齿轮和磨损5%齿轮产生的原始振动信号。

从基本Morlet小波的1～64尺度中提取小波系数的统计参数。这些统计特征定义如下［14-16］：

均值：信号的平均值；

幅值：信号最大值与最小值的差；

标准差（STD）：表示相对于均值的偏离程度，表达式如下，

偏度：是数据关于样本均值不对称性的度量。例如，如果偏度为负值，说明数据分散在左边多于右边，

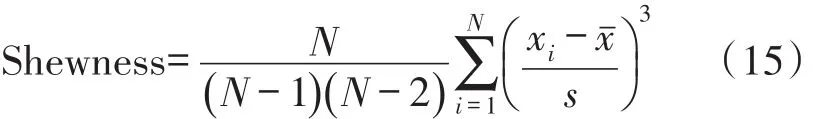
峰度：是概率密度分布曲线在平均值处峰值高低的度量，

图5　启动阶段，正常、有缺口、磨损10%和磨损5%齿轮情况时，齿轮箱的加速度信号

图6显示了连续小波变换尺度1～64的每个尺度下，正常、有缺口、磨损10%和磨损5%齿轮的STD、偏度和峰度因子曲线。可以看出正常和故障条件下的特征分布，当特性分离度越大，则该特征更能有效区分正常和故障情况。在一些尺度下特征有很高的分离度，我们将这些尺度命名为“最优尺度”。

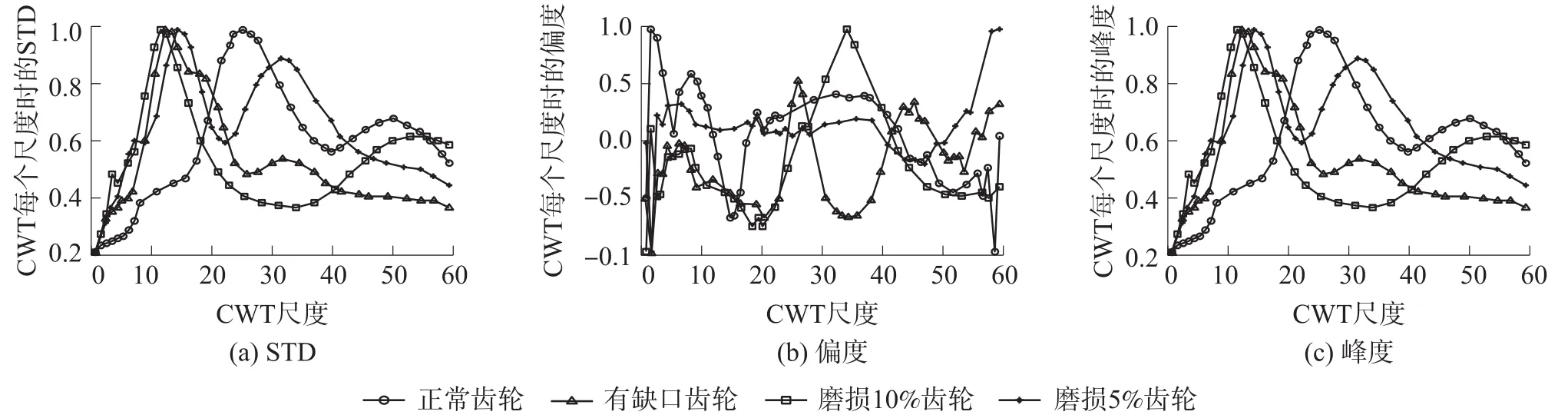
图6　在不同CW T尺度下，正常、有缺口、磨损10%和磨损5%齿轮的特征分布

确定尺度的最优数量，有利于缩减特征，本文采用小波熵和能量来选择最优尺度的基本Morlet小波。当相应的小波系数的香农熵最小且能量最大时，选择该尺度为最优尺度［17］。能量和香农熵的比值表达式如下：

信号在每个分辨率尺度‘n'上的‘m'个数量的小波系数能量记为：衡量信号小波系数不确定性的香农熵定义为：

式中，Pi为对应于每个系数的能量概率分布，且由下式确定：

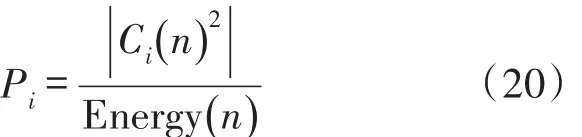
香农熵提供了一种分析和测量概率分布之间的相似度或不相似度的实用标准［18］。故障齿轮的测试信号在振幅和频率上都会变的有所不同，这也就使得测齿轮振动信号的能量和香农熵的分布也会相应地改变。由于能量和香农熵提取了信号信息，且小波算法能有效的进行非平稳信号的时频分析，所以将小波和能量、香农熵相结合，使其能够有效的分析故障信号。

图7　对于正常、有缺口、磨损10%和磨损5%齿轮条件下的连续小波变换的尺度水平下的能量和香农熵分布

对于正常、有缺口、磨损10%和磨损5%齿轮的CWT，1到64个尺度下的能量和香农熵分布如图7所示。为了找到最优尺度，对于正常齿轮，在1到64个尺度下的能量和香农熵比值如图8所示。

可以看出，能量与香农熵的比值较大区域的尺度为17～40，所以设定最优尺度为17～40。图9显示了最优尺度（17～40）时的能量和香农熵分布。图9可以看出，此时正常和故障情况的特征具有较大的分离度，有利于提高识别精度。

图8　对于正常齿轮，不同CW T尺度下的能量和香农熵分布

图9　对于正常、有缺口、磨损10%和磨损5%齿轮，在CWT最优尺度下的能量和香农熵分布

2.3故障分类实验

利用前馈多层感知器（MLP）神经网络（ANN）来分类正常和故障齿轮信号。本文考虑了3种场景下的输入数据和特征集来用于分类，如表1所示。在场景A中，不进行特征缩减，使用CWT所有尺度（1-64）下的统计参数，并将其作为特征集。场景B中，使用基于最大能量香农熵比确定的最优尺度（17-40）的统计特征。场景C中，除了使用最优尺度（17-40）下的统计特性，还将能量和香农熵加入特性集，作为两个新的特征。

表1　3种不同的场景作为ANN的输入

实验中，用所有尺度下的统计参数的1700个特征集来训练一个三层人工神经网络（ANN），用3 400个特征集作为测试数据。对于场景A，输入层有7个神经元，其中5个统计参数为均值、全距、标准差、偏度和峰度因子，另外两个输入为轴的旋转数和尺度数。场景B中，最优尺度的选择缩减了66%的特征，训练特征集为630个，测试数据集为1 360个。场景C在场景B的基础上，添加了能量和香农熵因子作为ANN输入的两个新特性那么场景C中ANN输入层为9个神经元。设定所有场景下，隐层的神经元的数量为20。

3种场景下的训练和测试准确度如表2所示，可以看出，采用最大能量香农熵比（最优尺度）缩减特征的方法（场景B），识别准确度比场景A提高了大约12～17个百分点，且ANN的训练时间缩减约2.6倍。另一方面，在最优尺度下，添加能量和香农熵作为两个新特性（场景C），使识别准确度比场景A增加20～30个百分点，比场景B也提高了5～11个百分点。

表2　场景A、B和C下的各种故障分类性能

3　结束语

本文提出了一种结合Morlet小波和MLP神经网络的齿轮故障检测方法。利用角域技术，将时域中齿轮故障的非平稳振动信号转化为角域中的平稳信号。然后，利用Morlet小波并从小波系数中提取统计特征。根据最大能量与香农熵比来寻找CWT的最优尺度，以此来缩减特征量，并将能量和香农熵作为两个新特征添加到特征向量。最后，利用MLP神经网络对输入特征进行分类，从而检测故障类型。实验结果表明，在最优尺度下，故障检测性能提高了12个～17个百分点，且大大缩短了训练时间。在添加2个新特征后，分类准确性又增加了5个～11个百分点。从而证明本文方法具有分类准确性高，计算速度快等优点，为齿轮箱故障检测提供了一种有效方法。

在今后工作中，将考虑检测齿轮箱符合故障，包括齿轮和电机轴承等故障。

［1］ 邵忍平，曹精明，李永龙.基于EMD小波阈值去噪和时频分析的齿轮故障模式识别与诊断［J］.振动与冲击，2012，31（8）：96-101.

［2］ 梅检民，肖云魁，贾继德，等.基于改进阶比的变速器微弱故障特征提取［J］.振动工程学报，2012，25（3）：317-322.

［3］ Sugumaran V，Rao A V，Ramachandran K I.A Comprehensive Study of Fault Diagnostics of Roller Bearings Using Continuous Wavelet Transform［J］.International Journal of Manufacturing Systemsand Design，2015，21（1）：27-46.

［4］ 顾煜炯，宋磊，苏璐玮，等.基于多元角域指标离群检测的风电齿轮箱故障预警方法［J］.振动与冲击，2015，34（1）：80-87.

［5］ Li H，Zhang Y，Zheng H.Angle Domain Average and CWT for Fault Detection of Gear Crack［C］//Fuzzy Systems and Knowledge Discovery，2008.FSKD'08.Fifth International Conference on. IEEE，2012：137-141.

［6］ Bafroui H H，Ohadi A.Application ofWavelet Energy and Shannon Entropy for Feature Extraction in Gearbox FaultDetection Under Varying Speed Conditions［J］.Neurocomputing，2014，133 （8）：437-445.

［7］ 李晓静，李杰.改进的小波神经网络在变压器故障诊断中的应用［J］.电子器件，2013，36（3）：404-407.

［8］ 王宁波，任伟新，贺文宇.桥上移动车辆车轴识别小波变换方法［J］.振动工程学报，2013，26（4）：539-544.

［9］ShatnawiY，Al-khassaweneh M.FaultDiagnosis in InternalCombustion Engines Using Extension Neural Network［J］.IEEE Transactionson Industrial Electronics，2014，61（3）：1434-1443.

［10］单亚峰，孙璐，付华，等.基于小波包和RBF神经网络的瓦斯传感器故障诊断［J］.传感技术学报，2015，28（2）：278-283.

［11］孙文胜，陈宇洋.BP神经网络在智能家庭网关中的应用研究［J］.电子器件，2013，36（1）：109-111.

［12］Liao TW，Chang E T&P C.Detection of Welding Flaws with MLP Neural Network and Case Based Reasoning［J］.Intelligent Automation&SoftComputing，2013，9（4）：259-267.

［13］Noekhah S，Hozhabri A A，Rizi H S.Software Reliability Prediction Model Based on ICA Algorithm and MLP Neural Network ［C］//E-Commerce in Developing Countries：With Focuson e-Security（ECDC），2013 7th Intenational Conference on IEEE，2013：1-15.

［14］蒋永华，汤宝平，董绍江.自适应Morlet小波降噪方法及在轴承故障特征提取中的应用［J］.仪器仪表学报，2011，31（12）：2712-2717.

［15］Li H M，Cai Z Z，An G.A Demodulating Approach Based on Local Mean Decomposition and Combined MorletWavelets and Its Application in Mechanical Fault Diagnosis［J］.Applied Mechanics&Materials，2013，26（7）：239-240.

［16］唐曦凌，梁霖，高慧中，等.结合连续小波变换和多约束非负矩阵分解的故障特征提取方法［J］.振动与冲击，2013，32（19）：7-11.

［17］Kankar P K，Sharma S C，Harsha S P.Fault Diagnosis of Ball Bearings Using Continuous Wavelet Transform［J］.Applied Soft Computing，2011，11（2）：2300-2312.

［18］李奕，吴小俊.香农熵加权稀疏表示图像融合方法研究［J］.自动化学报，2014，40（8）：1819-1835.

合尼古力·吾买尔（1976-），女，维吾尔族，新疆人，新疆交通职业技术学院副教授，博士研究生在读，研究领域为故障检测、网络安全等，wumeierxj@126.com。

A Gearbox Fault Detecting Method Based on Morlet Wavelet Transform and MLPNeural Network

HENIGULI·Wumaier1，2*，LIN Ling3，4
（1.Department of Mechanic and Electronic Engineering，Nanjing Uniυersity of Aeronauticsand Astronautics，Nanjing 210016，China；2.Department of transportmanagement，Xinjiang Vocational&Technical College of Communications，Urumqi 831401，China；3.Department of Electronicsand Information Engineering，YiliNormal Uniυersity，Yi'ning Xinjiang 835000，China；4.Department of Computer Scienceand Technology，Nanjing Uniυersity，Nanjing 210046，China）

For the issues that the fault detection of gearbox，amethod of gearbox fault diagnosis based on Morlet wavelet transform and MLP neural network is proposed.Firstly，the angular domain technique is used to transform the non-stationary vibration signals of the gear fault in time domain into stationary signal in the angular domain. Then，Morlet wavelet is used to extract statistical features from wavelet coefficients，and determines the optimal scale of continuouswavelet transform（CWT）according to themaximum energy and Shannon entropy ratio，in order to reduce the amount of features，at the same time，the energy of thewavelet coefficients and Shannon entropy can be regarded as two new features added to the feature vector.Finally，MLP neural network is used to classify the input features，so as to diagnose fault types.The experimental results show that thismethod has high accuracy of fault diagnosisand high calculation speed.

gearbox；fault detection；morletwavelet transform；multi-layer perceptron；neural networks；shannon entropy

TP391

A

1005-9490（2016）04-0834-07

2015-08-30修改日期：2015-10-08

EEACC:721010.3969/j.issn.1005-9490.2016.04.017