煤层气直井压裂参数优化设计

熊文学，袁　旭，惠　涛，王圣涛，刘　挺，申　超

(陕西延长石油国际勘探开发工程有限公司，陕西西安 710075)



煤层气直井压裂参数优化设计

熊文学，袁旭，惠涛，王圣涛，刘挺，申超

(陕西延长石油国际勘探开发工程有限公司，陕西西安 710075)

考虑煤层气直井压裂近井地带裂缝中的非达西紊流效应及气、水两相流动特征，结合水力压裂裂缝中净压力约束、最小缝宽约束的限制条件，建立了完整的煤层气储层直井压裂裂缝水力参数优化设计方法。在常规气藏物质平衡法的基础上，建立了基于煤层气储层的物质平衡法的生产动态预测模型，并对压裂直井的生产动态进行预测。研究结果表明，直井压裂裂缝中非达西紊流效应对产能的影响明显，高渗透煤储层中紊流降低支撑剂有效渗透率来减小裂缝导流能力，对气井产能起到很大的负面影响。高渗透煤储层易形成短而宽的裂缝几何形态，低渗透煤储层易形成长而窄的裂缝几何形态。产能对比和经济评价指标表明，煤层气压裂直井数越多，越有利于动用储量和提高经济效益，净现值越高，投资回收期越短。设计结果为煤层气直井压裂产能评价和优化设计提供了理论指导。

煤层气储层；直井压裂；物质平衡法；生产动态；参数优化

全球煤气层资源量可达260×1012m3，中国是世界上第三大煤层气储量国[1]，煤层气储量约为36.8×1012m3。虽然煤层气开采利用近年来发展较快，但煤层气在中国一次性能源消费结构中占有比例却很低，主要原因是目前煤层气开发技术不适应中国煤层气储层特点。煤层气井近井地带的紊流效应和气、水两相流动会降低气井产能，而目前将水力压裂应用于煤层气储层，提高煤层气井产能的研究还很少。Valkó 和Economides[2-3]提出了统一压裂设计方法，指出通过对水力压裂裂缝几何参数优化可以获得最大产能。J.A. Daal等[4]采用直接边界法计算不同形状比ye/xe(其中，ye为油藏控油面积的y方向边长；xe为油藏控油面积的x方向边长)储层的最优裂缝几何参数。Demarchos, A. S.等[5]提出在水力压裂优化设计中需要考虑约束条件的限制。Y. Wei 等[6]在水平井横向裂缝优化设计的研究中提出气井非达西效应对产能的影响不能忽略。

对于煤层气直井水力压裂优化设计，目前的研究存在以下不足：①针对煤层气储层特点的压裂优化设计理论及方法不完善；②没有煤层气直井压裂优化设计方案进行综合评价。本文针对煤层气直井水力压裂完井进行参数优化设计，并结合产能和经济评价对水力压裂优化方案进行评价，为压裂现场施工和煤层气有效开发提供理论依据。

1 煤层气直井压裂优化设计

1.1 优化设计流程

借鉴统一压裂设计原理，考虑煤层气直井压裂近井地带非达西紊流及气、水两相流动，综合考虑净压力约束、最小缝宽约束和经济评价指标，给出了完整的煤层气直井压裂裂缝水力参数优化设计方法。实现了给定支撑剂量时，对压裂直井分布、无量纲裂缝导流能力、无量纲生产指数、缝长、缝宽的优化设计，并结合净现值和投资回收期评价确定最优支撑剂量。优化设计流程如图1所示。

1.2 煤层气直井压裂优化设计理论

1.2.1 支撑剂数

支撑剂数是重要参数，关联最优裂缝导流能力和最大无量纲生产指数。在给定支撑剂注入量下，存在唯一特定裂缝几何形态时的压裂井生产指数最大[7-9]。

(1)

式中Np——无量纲支撑剂数；

Kf——裂缝支撑剂渗透率，mD；

K——储层渗透率，mD；

Vp——目标储层内支撑裂缝体积，该体积包括裂缝两翼支撑剂之间的孔隙体积，m3；

Vr——储层供给体积，m3。

1.2.2 最大无量纲生产指数和最优无量纲裂缝导流能力

最大无量纲生产指数JDmax和最优无量纲裂缝导流能力CfDopt的计算需要根据无量纲支撑剂数Np来确定。

(1)当Np<0.1时：

(2)

CfDopt=1.6

(3)

式中CA——Dietz形状系数(表1)。

表1所列的形状系数适用于方形或矩形封闭边界储层。

表1　不同储层形状比ye/xe下Dietz形状系数CA表

(2)当Np≥0.1时：

(4)

(5)

其中：

(6)

uopt=lnCfDopt

(7)

(8)

(9)

式中a、b、c、d、a′、b′、c′——有关形状因子相关系数(表2)。

1.2.3 最优支撑裂缝半长和缝宽

求得最优无量纲裂缝导流能力之后，最优支撑裂缝半长和缝宽可由下式获得。

表2　形状因子相关系数表

(10)

(11)

其中：

Vf=Vp/2

式中xfopt——最优支撑裂缝半长，m；

wfopt——最优支撑裂缝缝宽，m；

Vf——目标储层内支撑裂缝单翼体积，m3；

h——储层厚度，m。

1.2.4 非达西效应

气藏与油藏最大的区别之一在于气藏近井地带非达西渗流效应比较明显，而在油井中一般可以忽略。压裂直井裂缝与井筒接触面积小，裂缝汇聚流中紊流效应更严重，因此压裂直井产气能力被一定程度地削弱，根据非达西效应渗流公式可推导出有效裂缝支撑剂渗透率。

(12)

(13)

式中Δp——单位压差，MPa；

ΔL——单位长度，m；

μg——储层条件下气体黏度Pa·s；

v——储层条件下气体流动速度，m/s；

β——非达西系数，m-1；

ρg——气体密度，g/cm3；

Kf,e——有效裂缝支撑剂渗透率，mD。

Geertsma(1974)定义了孔隙介质雷诺数NRe，即：

(14)

(15)

1.2.5 约束条件

净压力和对最优裂缝几何参数构成限制约束。统一压裂设计中约束条件主要有以下两个：①压裂过程中，当最优裂缝设计过宽时，为了使裂缝支撑剂承受的最大净压力小于6.895MPa，引入最大净压力约束调整系数Factor1适当减少缝宽；②裂缝宽度应至少为支撑剂直径的3倍，以避免过早脱砂，当最优裂缝设计过窄时，引入最小缝宽约束调整系数Factor2适当增大缝宽。

(16)

其中：

w≥3Dp

(17)

式中Δpn——裂缝内净压力，MPa；

E′——平面应变，MPa；

Bp——支撑剂体积系数，m3/m3；

w——裂缝宽度，m；

Dp——支撑剂直径，mm。

2 煤层气直井压裂产能预测模型

2.1 煤层气储层物质平衡方程

煤层气以吸附气为主，随着排水降压的不断进行，气体从基质中解吸进入煤层割理系统产出地面，煤层中的流体流动一般经历单相水—气水两相—单相气流动阶段，基于上述排采过程，建立基于煤层气储层的物质平衡方程[10]。

煤储层累计产气量Gp为煤储层原始气储量Gi减去煤储层剩余气量Gr，即：

Gp=Gi-Gr

(18)

其中：

(19)

(20)

式中A——供给面积，m2；

φi——原始裂隙孔隙度；

Zsc——标准状况下气体偏差系数；

Tsc——标准状况下温度，K；

pi——储层原始压力，MPa；

ρB——煤岩密度，g/cm3；

VLdaf——无灰分、干煤层Langmuir体积系数，cm3/g；

α——平均灰分；

W——平均平衡湿度；

psc——标准状况下压力，MPa；

T——储层温度，K；

Swi——水相原始饱和度；

Z——气体偏差系数；

cf——当前压力下的煤割理体积压缩系数，MPa-1；

p——储层压力，MPa；

pL——Langmuir压力常数，MPa。

引入由King提出的非常规气藏气体偏差因子Z*，即：

(21)

式(18)可以变形为：

(22)

2.2 煤层气井气流量

通过引入真实气体拟压力函数，结合压裂优化设计求得的无量纲生产指数，可获得拟稳态条件下煤层气平面径向流产能计算公式：

(23)

式中qg——煤层气井日产气量，m3；

Kg——气体渗透率，mD；

m(pR)——平均油藏压力，MPa；

m(pwf)——井底流动压力，MPa；

m(pwf)——煤层温度，K；

JD——无量纲生产指数。

2.3 煤层气井生产动态预测

根据一口井的储层物性参数，通过物质平衡法预测煤层气井产能，步骤如下：

(1)结合煤层气储层的物性参数，计算原始压力条件下的气体偏差因子Zi，气体黏度μgi，气体的地层体积系数Bgi及原始气储量Gi。

(4)计算压力为p2时对应的压缩因子Z2，气体黏度μg2，气体体积系数Bg2。

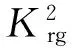
3 应用实例

煤层气储层参数及裂缝支撑剂参数较多，压裂参数优化及生产动态预测模型求解过程中所涉及的参数见表3。

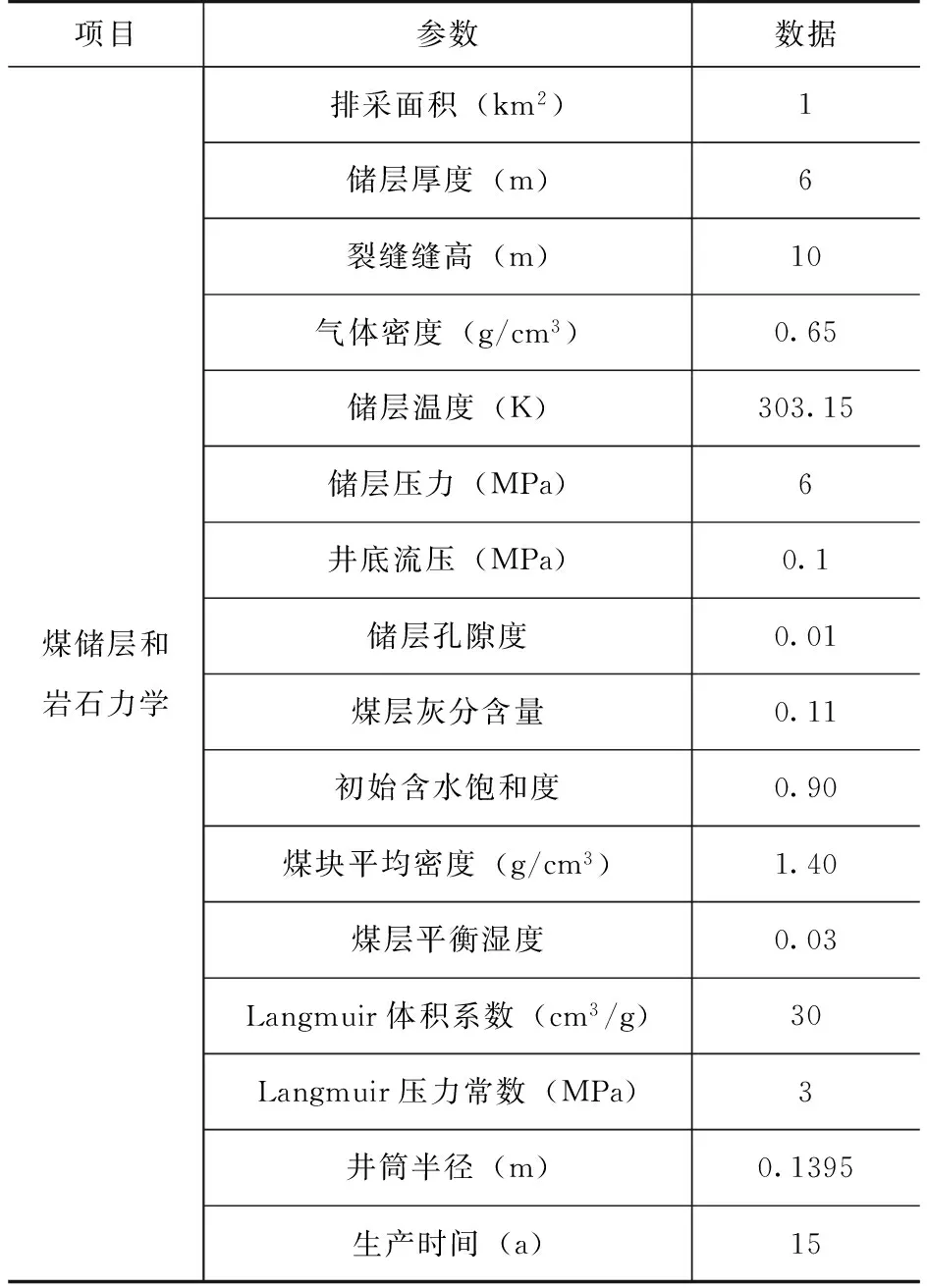
表3　煤层气储层物性、支撑剂和压裂液参数表

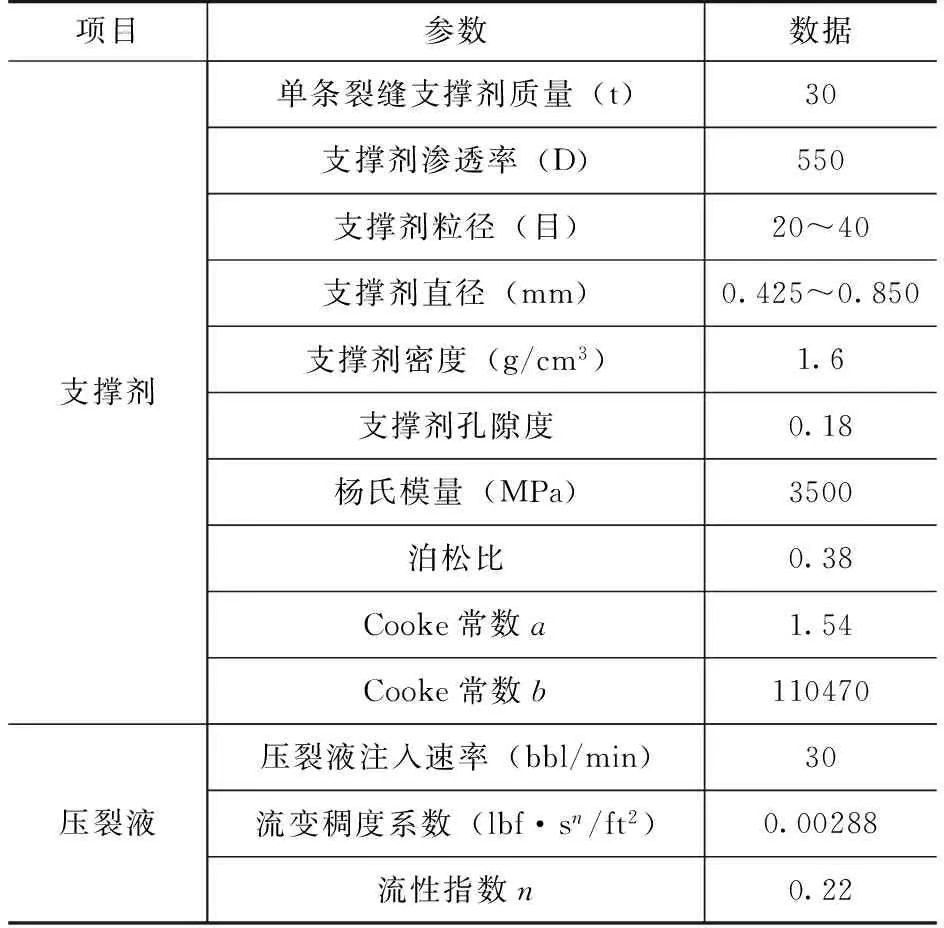
续表

注：1lbf·sn/ft2≈47900mPa·sn。

在压裂优化设计应用实例中，考虑了不同储层渗透率(0.01mD、0.1mD、1mD、10mD)条件下的设计方案，同时选取的实例包括5种布井方式对应的形状因子ye/xe条件下的压裂直井(图2)。

3.1结果分析

结合煤层气物质平衡数学模型和统一压裂优化设计的理论，考虑气井非达西效应、裂缝最大净压力约束和最小缝宽约束，通过Matlab编程对模型求解，在不同储层渗透率条件下对所有布井方式进行裂缝参数优化。优化结果如表4所示。

由表4可知，在其他条件相同的情况下，储层渗透率越高，对应的雷诺数NRe越大，即非达西紊流效应越明显，从而使得单井无量纲生产指数JD越小，因此储层的渗透率越高，压裂直井的产气优势越弱。当储层渗透率较高时，容易形成短而宽的裂缝，由于裂缝净压力与缝宽成正比，当裂缝净压力大于6.895MPa时，需要通过裂缝调整系数Factors1对缝宽进行调整，适当降低缝宽使裂缝净压力满足约束条件；当储层渗透率较低时，容易形成长而窄的裂缝，裂缝存在最小缝宽限制以避免出现砂桥，此时需要裂缝调整系数Factor2适当增大缝宽，以满足最小缝宽约束条件。

注：CfD—无量纲裂缝导流能力；xf—支撑裂缝半长；wf—支撑裂缝缝宽；Factor1和Factor2—约束调整系数。

3.2 产能对比

图3为Kf=550D、K=1mD、不同布井方式对应的日产气量和累计产气量与生产时间的关系曲线，从中可以看出，储层渗透率和泄气面积一定时，压裂直井井数越多，无量纲生产指数越大，日产气量和累计产气量越高，越有利于动用煤层气储量。

3.3 经济评价

3.3.1 净现值

净现值是指按设定的折现率，将项目计算期内各年发生的净现金流量折现到计算初期，求得的现值累计之和。其计算公式为[11]：

(24)

式中NPV——净现值，百万元；

C1——现金流入量，百万元；

C0——现金流出量，百万元；

i0——折现率；

t——计算期的年序号；

n——计算期。

3.3.2 投资回收期

投资回收期是指从项目投建之日起，用项目所得的净收益偿还原始投资所需要的年限，就是使累计经济效益等于最初的投资费用所需的时间。投资回收期反映项目资金周转速度，投资回收期越短，说明资金周转速度越快，风险越小[12]。

投资回收期(动态)=(t-1)+{第(t-1)年的累计净现值绝对值÷[第(t-1)年的累计净现值绝对值+第t年的折现值]}。

对于渗透率为0.1mD和1mD的煤层气储层，压裂井数越多，可获得的净现值越大；储层渗透率较低时(K=0.1mD)的净现值小于相同条件下储层渗透率较高(K=1mD)的净现值，原因是储层渗透率较低时，压裂直井产能较小，使现金流入减少，净现值降低(图4a)。

由图4b可见，压裂井数越多，投资回收期越短，资金回收速度越快。储层渗透率较低时(K=0.1mD)的投资回收期大于相同条件下储层渗透率较高时(K=1mD)的投资回收期，原因是储层渗透率较低，压裂直井产能较小，使现金流入减少，资金回收速度变慢。

4 结　论

(1)利用统一压裂设计的基本原理，考虑煤层气生产过程中的气井非达西效应、净压力约束及最小缝宽约束，在给定支撑剂量条件下对裂缝几何参数进行优化，获得压裂直井最优化裂缝导流能力和最大无量纲生产指数，并结合煤层气储层物质平衡法对压裂井生产动态进行预测。

(2)煤层气储层中非达西紊流效应明显，特别是在高渗储层中，紊流对气井产能起到很大的负面影响。紊流效应通过降低支撑剂有效渗透率来减小裂缝导流能力，减小气井生产指数，降低产气量。

(3)高渗透储层易产生宽而短的裂缝，低渗透储层易产生窄而长的裂缝。约束条件的控制对裂缝的几何尺寸起到调整作用，可以避免裂缝过宽超过最大净压力限制和裂缝过窄不满足最小缝宽约束。约束条件的限制对气井无量纲生产指数影响较小。

(4)经济评价结果表明，压裂井分布对净现值和投资回收期的影响较大，压裂井数越多，净现值越大，投资回收期越短。储层渗透率较低时，投资回收期较长，资金回收较慢，净现值为负。

[1]李军，赵文光，李娜，等. 煤层形成背景与煤层气储层特征[J]. 非常规油气, 2015, 2(2): 27-33.

[2]Economides M J, Oligney R E, Valkó P. Unified Fracture Design [M]. Orsa Press, Alvin TX, 2002.

[3]Economides M J, Oligney R E, Valkó P. Applying Unified Fracture Design to Natural Gas wells [J]. World Oil, 2002，223：50-62.

[4]Daal J A, Economides M J. Optimization of Hydraulically Fractured Wells in Irregularly Shaped Drainage Areas [C]. SPE 98047, at the 2006 SPE International Symposium and Exhibition on Formation Damage Control, Lafayette, LA, February 15-17, 2006.

[5]Economides M J, Demarchos A S. Pushing the Limits of Hydraulic Fracturing in Russia [C]. SPE 90357, at the 2004 SPE Annual Technical Conference and Exhibition, Houston, Texas, U.S.A. September 26-29，2004.

[6]Wei Y， Economides M J. Transverse Hydraulic Fractures From a Horizontal Well [C]. SPE 94671, at the SPE Annual Technical Conference and Exhibition, Dallas, Texas, U.S.A. October 9-12，2005.

[7]夏富国，郭建春，袁浩仁，等. 基于支撑剂数的压裂优化设计方法研究[J]. 国外油田工程, 2010，26(10): 20-22.

[8]蒋廷学，胥云. 低渗透油藏基于支撑剂数的压裂优化设计方法研究[J].石油钻采工艺，2008，30(3)：87-89.

[9]尹锦涛,田杰苗,孙建博，等. 煤层气水力压裂增产机理及效果评价方法研究[J]. 非常规油气, 2015, 2(5): 72-76.

[10]张健，汪志明. 物质平衡法在煤层气藏生产动态预测中的应用[J]. 煤田地质与勘探, 2009，37(3): 23-26.

[11]魏宝香. 关于提升净现值在项目投资评价中运用的研究[J]. 经济问题，2013(6)：95-98.

[12]王晶香，张雪梅. 建设项目财务评价指标-投资回收期浅析[J]. 建筑管理现代化，2004(2)：13-16.

The Parameter Optimization Design of CBM Vertical Fracturing Wells

Xiong Wenxue，Yuan Xu,Hui Tao,Wang Shengtao,Liu Ting,Shen Chao

(ShaanxiYanchangPetroleumInternationalExplorationandDevelopmentEngineeringCo.,Ltd，Xi′an,Shaanxi710075，China)

According to non Darcy turbulent flow effect and the characteristics of two-phase flow (gas and water) in the fractures near the wellbore have been considered in the fracturing of CBM vertical wells, combined with the restriction conditions of net pressure and minimum crack width in hydraulic fracturing, the optimization design method of hydraulic parameter for vertical well fracturing in CBM reservoir has been estabilished. On the basis of material balance method of conventional gas reservoir, the production performance prediction model for CBM was formed in terms of the balance method, so as to predict the production performance of vertical wells that treated by fracturing. Research results showed that the effect of non Darcy turbulent flow on the productivity in vertical well fracturing was obvious, and the turbulent flow in high permeability coal reservoir has reduced the effective permeability and conductivity that created by proppant, resulting in a great negative impact on gas well productivity. High permeability coal reservoir is easy to form short and wide fractures, but low permeability coal reservoir is easy to form long and narrow fractures. Production capacity comparison and economic evaluation index indicated that the more the CBM vertical wells by fracturing, the more beneficial to the use of reserves and improvement of economic efficiency, so the higher the net present value, the shorter the payback period of investment. The design results can provide the theoretical guide for evaluating production capacity and optimizing the design of CBM vertical well fracturing.

CBM Reservoir; Vertical Fracturing Wells; Material Balance Equation; Production Performance; Parameter Optimization

熊文学(1988年生)，男，助理工程师，现主要从事石油与天然气勘探开发研究和管理工作。邮箱：2120383656@qq.com。

TE323

A